数据结构、算法及线性表的总结
数据结构、算法及线性表的总结
思维导图
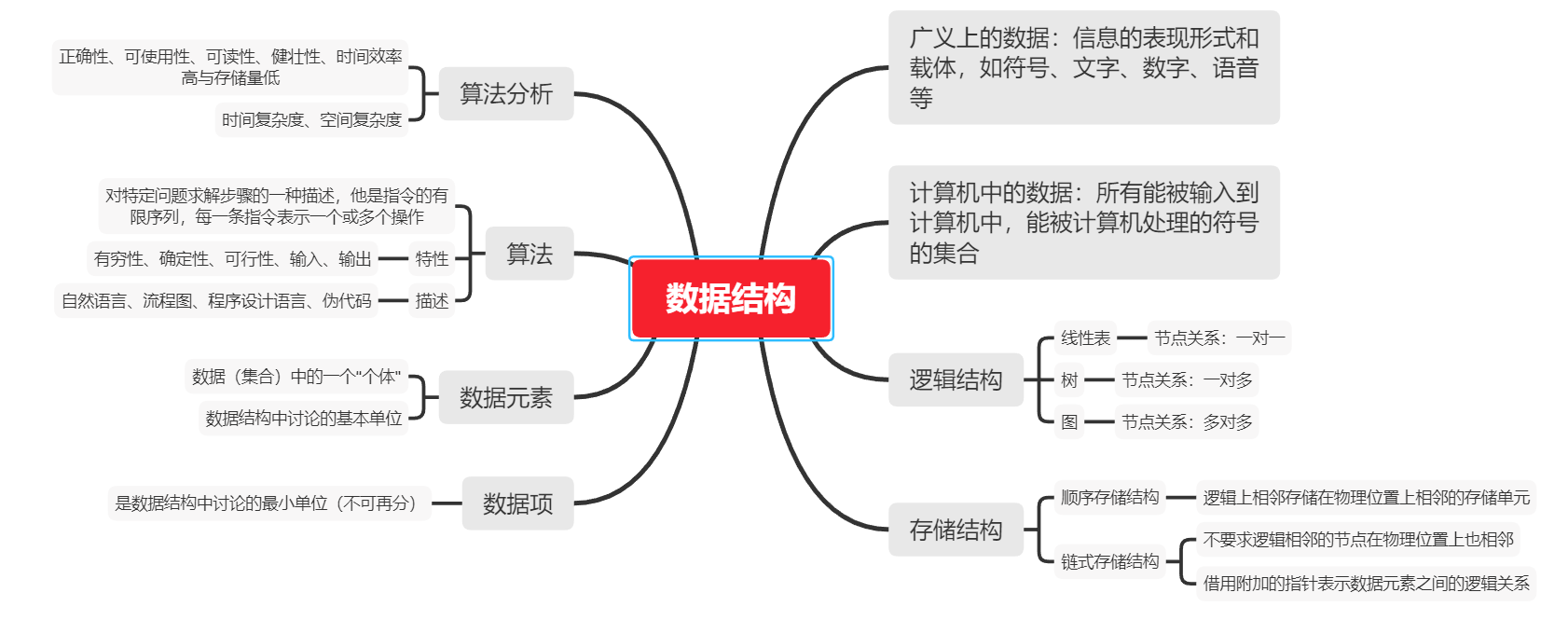
数据结构:
线性表:
重要概念的笔记
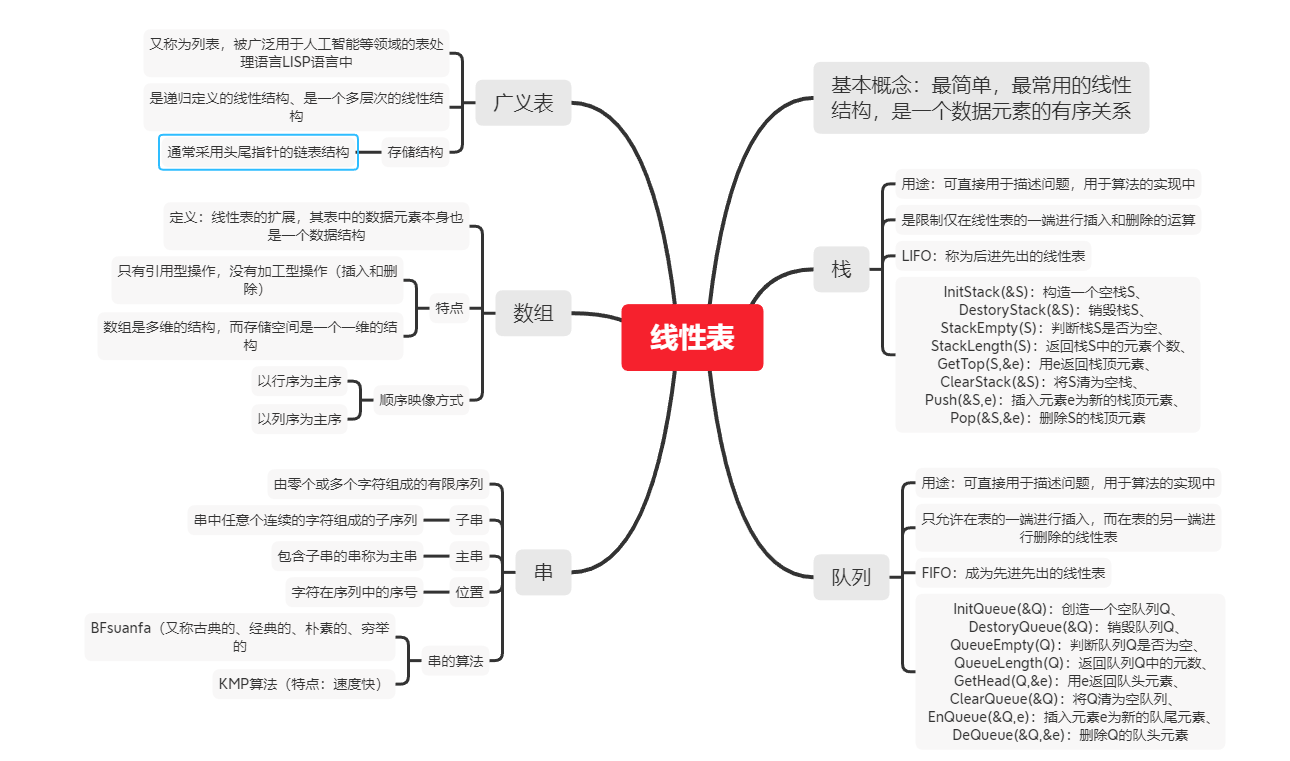
线性表
1.线性结构是一个数据元素的有序关系,掌握线性表的基本运算。
2.线性表的顺序存储是使用一块地址连续的存储空间,按照线性表中元素的逻辑顺序依次存放相应元素。
3.线性表的链式结构是将线性表中的数据元素存放在一组地址任意的存储节点,节点之间使用“链”进行连接。
4.链式结构中节点=数据元素+指针。数据元素:存放数据。指针:存放该节点下一个元素的存储位置。
5.顺序存储结构:支持随机访问,快速获取第j列的值。链式存储结构:灵活、不会造成存储空间的浪费。
6.有序表,是一种线性表,其中所有元素以递增或递减方式有序排列。
栈与队列
1.栈和队列是限定插入和删除只能在表的“端点”进行的线性表。
2.栈为后进先出线性表,只能在栈顶进行插入和删除操作。
3.队列为先进先出线性表,在队头进行删除,队尾进行插入操作。
4.链栈:插入和删除只能在表头进行、链栈中的结点是动态产生的,不考虑上溢问题、无需附加头结点,栈顶指针就是链表头指针。
5.掌握中缀表达式与前、后缀表达式的代换。
6.掌握用栈来解迷宫的算法。
7.递归与栈的关系。递归两大特点:自我调用、必须有递归出口。
8.循环队列判断队空:Q.rear=Q.front。判断堆满:(Q.rear+1)%m=Q.front。
串
1.串是由零个或多个字符组成的有限序列,一般记为:s='a1a2a3···an'(n>=0)。
2.串的数据对象约束为字符集、串通常以:串的“整体”作为操作对象。
3.用一组地址连续的存储带院存储串值的字符序列,成为顺序串,可用一个数组来表示。
4.存储密度=(数据元素所占存储位)/(实际分配的存储位)。
5.BF算法(又称古典的、经典的、朴素的、穷举的),KMP算法(特点:速度快)。
6.BF算法最坏情况下时间复杂度为O(n*m).
7.掌握next值和nextval值的计算方法。
8.KMP算法的优点:不需回溯,对于从外设读入的庞大文件很有效,可以边腐乳边匹配,无须回头重读。
数组和广义表
1.数组是线性表的扩展,其表中的数据元素本身也是一个数据结构。
2.数组的特点:只有引用型操作,没有加工型操作(插入和删除)、数组是多维 的结构,而存储空间是一个一维的结构。
3.矩阵可以用二维数组来储存。
4.对角矩阵:所有非零元素都计中在以主对角线为钟心的带状区域中。
5.将指示“行”信息的数组cpot固定在稀疏矩阵的存 储结构中,称这种“带行链接信息”的三元组表为 行逻辑链接的顺序表。
6.十字链表:当矩阵的非零元个数和位置在操作中变化较大时, 不宜采用顺序存储结构来表示三元组的线性表。
7.广义表又称为列表(lists),被广泛用于人工智能等领域的 表处理语言LISP语言中。
8.广义表是递归定义的线性结构,是一个多层次的线性结构。
9.广义表的结构特点:广义表中的数据元素有相对次序、广义表的长度定义为最外层包含元素个数、广义表的深度定义为所含括弧的重数、广义表可以共享、广义表可以是一个递归的表。
10.广义表通常采用头、尾指针的链表结构。
疑难问题及解决方案
7-1 jmu-ds-栈与队列-stack、queue与string小综合 (5分)

#include<string>
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
int main() {
string line;
char x;
int i, j;
stack<char> s;
queue<char> q;
cin >> line;
cin >> x;
for (i = 0;line[i] != '\0';i++) {
s.push(line[i]);
}
cout << s.size() << " ";
cout << s.top() << endl;
while (!s.empty()) {
cout << s.top();
if (s.top() != x) {
q.push(s.top());
}
s.pop();
}
cout << "\n" << q.size() << " " << q.front() << " " << q.back() << "\n";
while (!q.empty()) {
cout << q.front();
q.pop();
}
return 0;
}
在写这道题的过程中,对string的用法还不是很明确,一直在纠结该怎么读入一行的字符并且将它入栈,在老师发出的资料中进行了基础学习,直到了string可以定义一个字符串,并且将它作为数组使用,这样就可以用一个for循环将字符串中的字符一个个的入栈。
7-7 银行业务队列简单模拟 (25分)

#include<iostream>
#include<queue>
using namespace std;
int main(){
queue<int> q1,q2;
int n;
cin>>n;
while(n--){
int m;
cin>>m;
if(m%2)q1.push(m);
else q2.push(m);
}
while(!q1.empty()){
int cnt=2,i=0;
while(cnt--&&!q1.empty()){
if(i++)cout<<" ";
cout<<q1.front();
q1.pop();
}
if(!q2.empty()){
cout<<" "<<q2.front()<<" ";
q2.pop();
}
}
int i=0;
while(!q2.empty()){
if(i++)cout<<" ";
cout<<q2.front();
q2.pop();
}
return 0;
}
在写这道题的过程中,一直没有想出两个处理速度不一样的窗口的出队顺序,有点没有理解题目的意思,在查询了网上别人的答案后知道在A、B队列不为空时,总是A队列先出队两个元素在接着B队列出队一个元素,直到其中一个队列或者两个队列为空时,就直接把剩下的元素从队列中全部输出。
7-1 jmu-ds-最长数字序列 (25分)

#include<stdio.h>
#include<iostream>
#include<string>
using namespace std;
int main(){
string s;
getline(cin,s);
int maxindex = 0,maxlen = 0;
int len = 0;
if(s.length()==0){
cout << "NULL";
return 0;
}
for(int i = 0;i < s.length();i++){
if(s[i]>='0'&&s[i]<='9'){
len++;
if(s[i+1]=='\0'){
maxlen = len;
maxindex = i-len+1;
}
}
else{
if(len >= maxlen){
maxlen = len;
maxindex = i-len;
}
len = 0;
}
}
cout<<maxindex<<" "<<maxlen;
return 0;
}
在写这道题时并不清楚思路,该如何去计算一个字符串中的相连的数字元素的个数并从中筛选出最长串,本来想用一个数组来存储每串连续数字元素的个数,并从中输出最大的值,但是稍微有点麻烦,后来想到可以计算完一个连续数字元素的个数后就和前一个进行比较,然后用maxlen来表示目前最长串,首先判断元素是否为数字,用len来计算当前连续数字元素个数,直到下一个元素不为数字时,然后将len与maxlen比较,再让len=0,重复循环,最后得出最长串的连续数字。


