一、学习资料：
北京博雅数据酷客平台大讲堂：http://cookdata.cn/auditorium/course_room/10014/
二、概念
1、什么是分类：
另一种典型的有监督学习问题
标签（模型预测值）y为离散值
实际应用举例：
新闻主题分类：科技、教育、社会、体育？
疾病诊断：根据病人肺部影像图片，诊断是否患有COVID-19
市场营销：根据顾客历史购买记录和行为偏好，预测用户是否喜欢新产品
信用评估：根据客户历史信贷记录，预测贷款是否会违约
2、用回归解决分类
三种算法
2.1感知机（Perceptron)
概念：找到一条直线，讲两类数据分开即可
感知机算法（SGD）
2.2支持向量机（Support Vector Machines)
概念：找到一条直线，不仅将两类数据正确分类，还使得数据离直线尽量远
优化目标：
2.3逻辑回归（Logistic Regression)
概念：找到一条直线使得观察到训练集的“可能性”最大
3、损失函数对比
三、Sklearn分类模块介绍
四、案例学习
4.1、画点和相关直线
1、首先使用sklearn中的datasets模块生成一个随机的二分类数据集
from sklearn import datasets random_samples=datasets.make_classification(n_samples=60,#样本数量 n_classes=2,#类别数量 n_features=2,#特征数量 n_informative=2,#有信息特征数量 n_redundant=0,#冗余特征数量 n_repeated=0,#重复特征数量 n_clusters_per_class=1,#每一类的簇数 flip_y=0,#样本标签随机分配的比例 class_sep=3,#不同类别样本的分散程度 random_state=203)
2、为了便于后续处理，我们将生成的数据封装到Pandas的DataFrame中。数据集数据包含两个特征，特证名为x1和x2，标签值存放在label中。为了后续处理方便，我们给数据集添加一个取值全为1的ones
import pandas as pd data=pd.DataFrame(data=random_samples[0],columns=["x1","x2"]) data["label"]=random_samples[1] data["ones"]=1#添加一个取值全为1的列"ones" data.head()
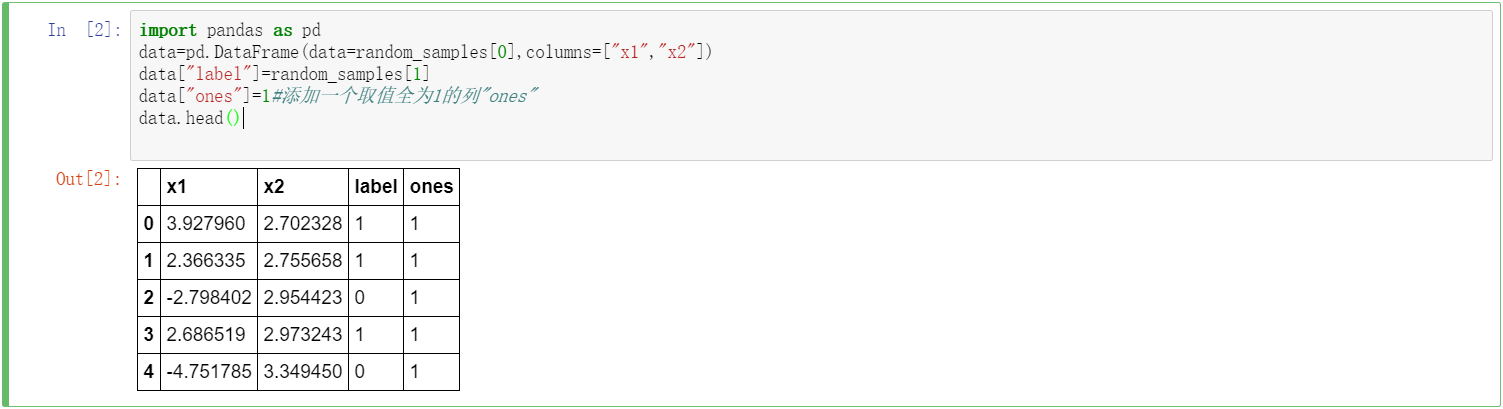
3、在本案例即将实现的算法中，我们假设标签取值为1或-1，观察上表label列取值可见，默认的取值为0或-1，应用map方法，我们将label列取值映射为1和-1
data["label"]=data["label"].map({0:-1,1:1})#将y的取值替换成1和-1
4、为了值观地了解数据，我们将数据集用散点图绘制出来。matplotlib.pyplot模块地scatter函数可以绘制散点图，他的主要参数为横轴数据x,纵轴数据y,点地颜色c,点的形状等marker
数据集中正样本和负样本需要进行区分，我们首先将他们进行分离
data_pos=data[data["label"]==1]#筛选出正样本 data_neg=data[data["label"]==-1]#筛选出负样本来
5、将绘图框大小设置成(8,8),然后将正样本化成洋红色（c="#E4007E")的三角形(marker="^")，将负样本化成深绿色（c="#007979")的图形（marker="o")
import matplotlib.pyplot as plt plt.reParam['axes.nuicode_minus']=False plt.figure(figsize=(8,8))#设置图片尺寸 plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^")#类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o")#类别为-1的数据绘制成深绿色
plt.xlabel("$x_1$")#设置横轴标签 plt.ylabel("$x_2$")#设置纵轴标签 plt.xlim(-6,6)#设置横轴显示范围 plt.ylim(1,5)#设置纵轴显示范围 plt.show()
6、画出直线
import numpy as np w=[1,1,-4] x1=np.linspace(-6,6,50) x2=(w[0]/w[1])*x1-w[2]/w[1]
4.2、利用感知机进行
另写博客：https://www.cnblogs.com/hhjing/p/14341646.html
4.3、梯度下降法求解逻辑回归
另写博客：https://www.cnblogs.com/hhjing/p/14341709.html
4.4、支持向量机实现
