一:运行代码,并分析结果
代码1:
package reserve; public class Main { public static void main(String[] args) { Size s=Size.SMALL; Size t=Size.LARGE; //s和t引用同一个对象? System.out.println(s==t); // //是原始数据类型吗? System.out.println(s.getClass().isPrimitive()); //从字符串中转换 Size u=Size.valueOf("SMALL"); System.out.println(s==u); //true //列出它的所有值 for(Size value:Size.values()){ System.out.println(value); } } }
enum Size{SMALL,MEDIUM,LARGE};
测试结果截图:

分析结果和结论:
1.对于枚举类型的变量,“==”和“equals()”方法执行的结果是等价的。
2.枚举的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。
3.枚举是常量,所以应该用大写;
4.枚举隐含地继承了java.lang.Enum,所以它具有java.lang.Enum的属性和方法;
5.for(Size value:Size.values()){
System.out.println(value);为遍历枚举,输出为 SMALL
MEDIUM
LARGE
6.getDeclaringClass() 方法返回和当前枚举常量的枚举类型对应的 class 对象
代码2:
package reserve; public class Main { public static void main(String[] args) { int X=100; int Y=200; System.out.println("X+Y="+X+Y); System.out.println(X+Y+"=X+Y"); } }
测试结果截图:

分析:“”里面的X+Y为字面量是不发生改变的,“”外面的运算符+将变量X+Y进行连接;
代码:3:
package reserve; public class Main { private static int value=1; public static void main(String[] args) { int value=2; System.out.println(value); } }
测试结果截图:

package hhj; public class Hhj{ public static int value=6; public static void main(String[] args) { int value=2; System.out.println(value); } }
测试结果:2
结论:在函数里面的赋值优先于在函数外赋值,函数外的赋值可以赋给类中的多个函数,如果函数里面没有重复的赋值,那么函数的值为函数外的。
代码4:
package reserve; public class Main { public static void main(String args[]) { System.out.println("0.05 + 0.01 = " + (0.05 + 0.01)); System.out.println("1.0 - 0.42 = " + (1.0 - 0.42)); System.out.println("4.015 * 100 = " + (4.015 * 100)); System.out.println("123.3 / 100 = " + (123.3 / 100)); } }
测试结果截图:

结论:使用double类型的数值进行计算,的出来的结果是不精确的。这个涉及到二进制与十进制的转换问题。double类型的数值占用64bit,即64个二进制数,除去最高位表示正负符号的位,在最低位上一定会与实际数据存在误差(除非实际数据恰好是2的n次方)。double类型后面舍去的位数一定会带来误差,从而不能得到“数学上精确”的结果。
二:原码,反码,补码解读
原码: 二进制定点表示法(八位),即最高位为符号位(左数第一位),“0”表示正,“1”表示负,其余位表示数值的大小(二进制)。

反码: 正数的反码与其原码相同。
负数的反码是对其原码依次取反(0->1,1->0),但是符号位除外。
补码:正数的补码与其原码相同
负数的补码是在其反码的末尾加一(用二进制的加法,注意1+1进位)。
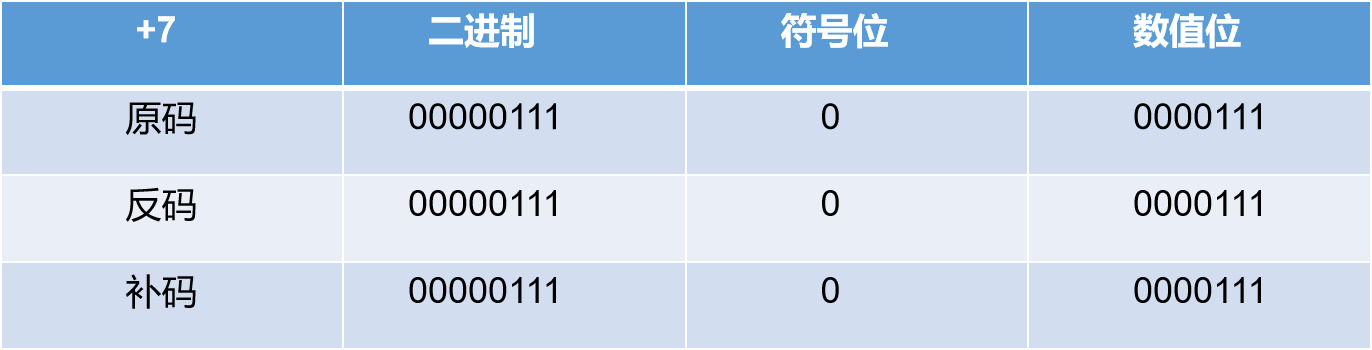
正数的原码,反码和补码是相同的。
正数举例:
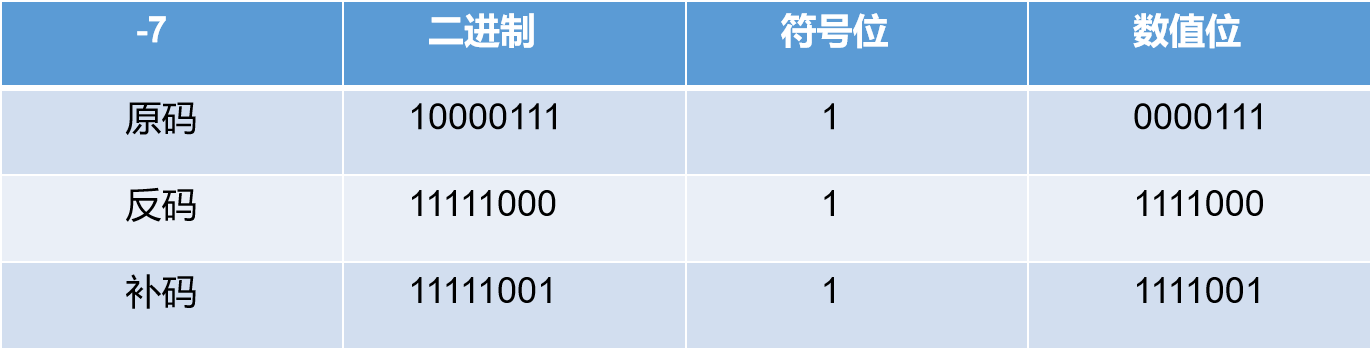
负数举例:
代码(十进制数转换成计算机识别的8位的二进制数):
package reserve; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int count[]=new int[8]; int j=0;//定义一个数量为8的数组用来存储二进制的数; System.out.println("请输入整数:"); int num = sc.nextInt(); System.out.println("原码:"); if(num>0) count[0]=0; else { count[0]=1; num=-num; } System.out.print(count[0]); String a = ""; //用字符串拼接 while(num!=0) { //利用十进制转二进制除2法 a=num%2+a; num=num/2; j++; } for(int k=1;k<8-j;k++) { count[k]=0; System.out.print(count[k]); } System.out.println(a); int math=Integer.parseInt(a); // String aS = String.valueOf(a); //char[] asC = aS.toCharArray();将字符串转换成整型 //String result = Integer.toBinaryString(num);//将十进制数转换成二进制数 } }
三:看看下图,再查看Java中的每个数据类型所占的位数,和表示数值的范围,写出所得的结论。
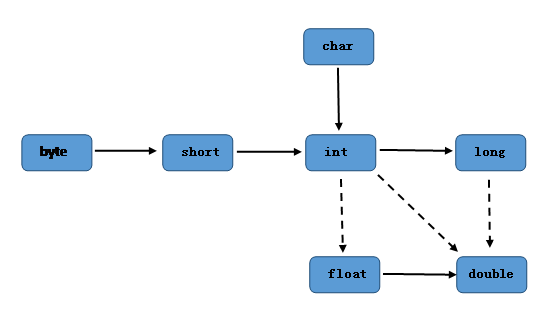
结论:每个数据类型所占的位数和表示数值的范围
byte:1字节 -128~127
short:2字节 -2^15~2^15-1
int :4字节 -2^31~2^31-1
long:8字节 -2^63~2^63-1
boolean:1字节 true false(java中不能以0或非0代替)
float: 4字节 -3.403E38~3.403E38
double:8字节 -1.798E308~- 4.9E324
char:2字节 ’\u0000‘~' ’\uffff '(16进制的,换算过来即0~65535)
(1字节等于8位)
实数代表无精度损失,虚线代表有精度损失。一般来说在实线两端都是由低精度指向高精度的类型,所占的位数从高到低,范围从小到大,所以可得出,低精度向高精度转化不丢失精度,反之,从高精度转向低精度则会损失。


