搜城探宝【树形DP】
搜城探宝【树形DP】
今天任务比较少,晚上莫名睡不着,果断选择写个题解再睡
题目描述
-
zhclk 已经坚信自己就是传说中的有缘人,于是,带着梦想,带着希冀,带着勇气,来到了神迹,寻找……
-
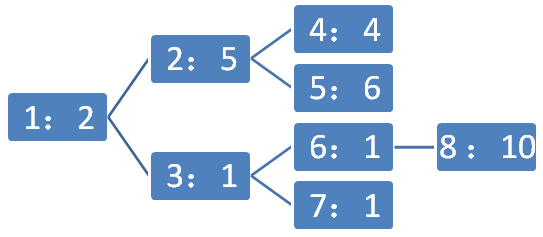
如下图,神迹的城堡是一个树形的结构,共有 nn 间屋子。每间屋子都有一把锁,并且每间屋子最多可以到另外的两个屋子里(它是一棵二叉树)。在城堡的每个房间都存在着不同的宝藏。现在 zhclk 站在城堡的大门口(11 号屋子门口)拥有 kk 把万能钥匙,可以打开任意一把锁,但每把钥匙只能用一次,钥匙是拔不出来的。
-
问题哪有那么简单……,Zhclk 还有一个传送门,可以在任何时候带他去任何一间屋子,但传送门也只能 使用一次。
-
地图上画出了宝藏的分布,只有获得最大价值的宝藏 zhclk 的目的才能实现。
Input
- 第一行:两个数
n和k。为城堡的屋子总数和你拥有的万能钥匙数。 - 第二行到第
n行:每行两个数x1和x2,为树上的n−1条边。(树保证以1为根节点)。 - 第
n+1行:n个数,第i个数为房间i的宝藏价值vi。
Output
- 一个数,为最大宝藏价值
maxv。
Sample Input
8 4
1 2
1 3
2 4
2 5
3 6
3 7
6 8
2 5 1 4 6 1 1 10
Sample Output
27
Hint
- 用钥匙依次开1,2,4,5 号房间,再用传送门去 88 号房间,27=2+5+6+4+10 。
- 数据范围: n<=20n<=20 。
思路分析
-
二叉树结构,求最大价值,树形DP无疑
-
关键点和特殊点:
- 🔑数限制住了可走的步数
- 有一个传送🚪,可以到达任何一个位置
-
处理方式:
- 将🔑数加入dfs的过程中,进行传递即可
- 有了传送🚪,其实我们有了一个直接蹦到某个祖先结点的任何一个子结点,从而任意获取其子树的最大价值
-
重点——虚根:
-
这题用到了一个非常巧妙的方法——设置虚根(相对于实根1而言),重要的是要保证这个虚根的增加不会破坏原有的树的结构,因为我们在添加虚根的时候并未修改结点之间的关系。
-
用完传送🚪以后到达的子树,可视为一个独立的子树,与其它的子树可以直接区分开,因为我们在其他子树的任意位置都可以来到传送🚪所在的子树,简单来说就是将传送🚪统领的子树''拔''出来差别对待
-
首先令
n+1的左儿子为1,然后从2到n枚举y(也就是被挂出去的节点),把y设置为n+1的右儿子,对树n+1进行一次树形dp。
-
代码
题库现在登不上去我只能先用老姚的代码了,虽然不知道对不对(不是)......注释改了改
#include <bits/stdc++.h>
const int maxn=20+5;
int n,k,a[maxn],ans=0;
int fa[maxn],ls[maxn],rs[maxn];
int dfs(int x,int sum){ //我们用sum记录此时所剩下的🔑数
if(x==0)return 0;//搜完叶子
if(sum==1)return a[x];//只剩下一把🔑,开完就没了
int now=0;
for(int i=0;i<sum;++i)//DP部分,左右子树各种可能分配的🔑情况
now=std::max(now,dfs(ls[x],i)+dfs(rs[x],sum-1-i)+a[x]);
return now;
}
void Init(){
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i){
int x,y;scanf("%d%d",&x,&y);
if(!ls[x])ls[x]=y;//直接建树不解释
else rs[x]=y;
fa[y]=x;
}
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
}
void Solve(){
ls[n+1]=1;//虚根,原根作为左儿子
for(int i=2;i<=n;++i){//枚举其他点,作为右儿子
rs[n+1]=i;//把i作为右儿子,增加钥匙一把
if(ls[fa[i]]==i){//i是左儿子
ls[fa[i]]=0;//先断掉
ans=std::max(dfs(n+1,k+2),ans);//增加了2把钥匙所以是k+2
ls[fa[i]]=i;//重新续上
}
else{//i是右儿子
rs[fa[i]]=0;//断掉
ans=std::max(dfs(n+1,k+2),ans);
rs[fa[i]]=i;//续上
}
}
printf("%d\n",ans);
}
int main(){
Init();
Solve();
return 0;
}
发量由于''肝帝debuff''减2%


