特殊方格棋盘【状压DP】
特殊方格棋盘【状压DP】
讲真状压DP这个东西只不过是有那么亿丢丢考验心态罢了(确信)
先从板子题说起,另加一些基础知识
题目描述
在的方格棋盘上放置n 个车,某些格子不能放,求使它们不能互相攻击的方案总数。
注意:同一行或同一列只能有一个车,否则会相互攻击
输入格式
输入文件第一行,有两个数n, m ,n表示方格棋盘大小,m表示不能放的格子数量
下面有m行,每行两个整数,为不能放的格子的位置。
输出格式
输出文件也只有一行,即得出的方案总数。
样例
样例输入
2 1
1 1
样例输出
1
思路分析
状压的核心:1. 二进制表示状态
2.位运算进行转移等操作
-
状压DP的核心就在于用二进制数表示一种状态,其实是一种非常暴力的算法,举个例子:
例如dp[s] [v]中,S可以代表已经访问过的顶点的集合,v可以代表当前所在的顶点为v。S代表的就是一种状态(二进制表示),比如 (11001)2 代表在二进制中{0,3,4}三个顶点已经访问过了,(11001)2 代表的十进制数就是25 ,所以当S为25的时候其实就是代表已经访问过了{0,3,4}三个顶点,那假如一共有5个顶点(标号为01234)的话,所有的顶点都访问完毕应该S为什么呢?是 (11111)2。
-
关于本题:
-
这题的约束条件非常非常简单,直接告诉了你哪里不能放,那么我们怎么记录这个所给的约束条件呢?
-
其实也是用二进制的思想,我们开一个数组a[x],表示第x行的限制,如果第x行的第y列不能放置,那么我们就将其对应的二进制位变为1,这里涉及到了位运算——
a[x] += 1<<(y-1); -
本题还用到了另一个和二进制紧密相关的东西:
int lowbit(int x){return x & -x;} 返回值是最后一个二进制数位为1的位置
-
-
转移方程:
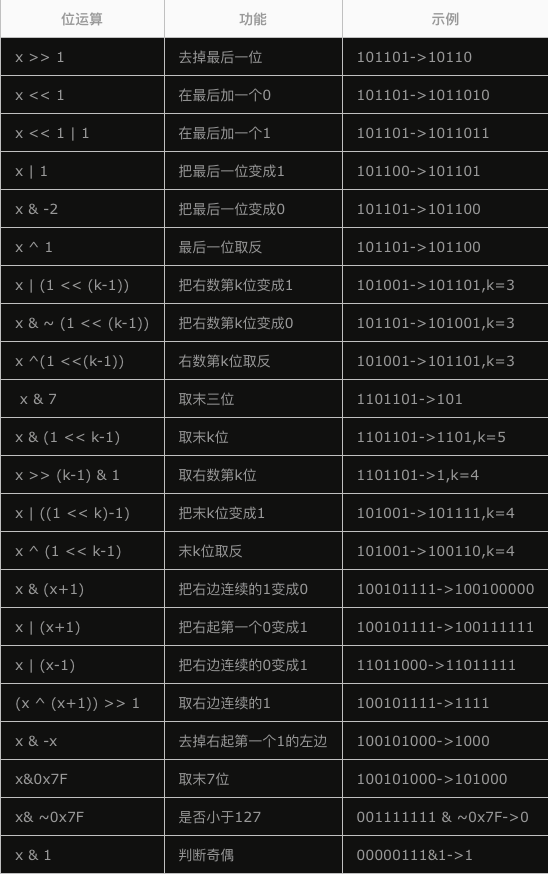
int maxs = 1<<n; //显然这是最大的状态,即每个二进制位都是1 for(int s = 1;s < maxs;s++){ int cnt = 0; for(int i = s;i;i-=lowbit(i))cnt++;//记录二进制1的个数,即放车车的个数(等于行数) for(int i = s;i;i-=lowbit(i)){ //根据不能放在同一列进行转移 if(!(a[cnt] & lowbit(i))){ //首先要保证该位置可以放 int ss = s^lowbit(i); //异或恰好使得上一行的状态与本行不发生冲突 f[s] += f[ss]; } } }另附一张位运算常用操作:
上代码
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> const int maxn = (1<<20)-1; typedef long long ll; ll f[maxn],a[25]; int lowbit(int x){ return x & -x; } int main(){ int n,m;scanf("%d%d",&n,&m); for(int i = 1;i <= m;i++){ int x,y;scanf("%d%d",&x,&y); a[x] += 1<<(y-1); } f[0] = 1; int maxs = 1<<n; for(int s = 1;s < maxs;s++){ int cnt = 0; for(int i = s;i;i-=lowbit(i))cnt++; for(int i = s;i;i-=lowbit(i)){ if(!(a[cnt] & lowbit(i))){ int ss = s^lowbit(i); f[s] += f[ss]; } } } printf("%lld\n",f[maxs - 1]); return 0; }
发量成功减1%


