[APIO2010]巡逻(树的直径)
[APIO2010]巡逻
题目描述
在一个地区中有 n 个村庄,编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄,每条道路刚好连接两个村庄,从任何一个村庄,都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全,巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里,每天巡警车总是从警察局出发,最终又回到警察局。 下图表示一个有 8 个村庄的地区,其中村庄用圆表示(其中村庄 1 用黑色的 圆表示),道路是连接这些圆的线段。为了遍历所有的道路,巡警车需要走的距 离为 14 个单位,每条道路都需要经过两次。
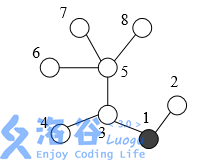
为了减少总的巡逻距离,该地区准备在这些村庄之间建立 K 条新的道路, 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 (见下面的图例(c))。 一条新道路甚至可以是一个环,即,其两端连接到同一 个村庄。 由于资金有限,K 只能是 1 或 2。同时,为了不浪费资金,每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子:
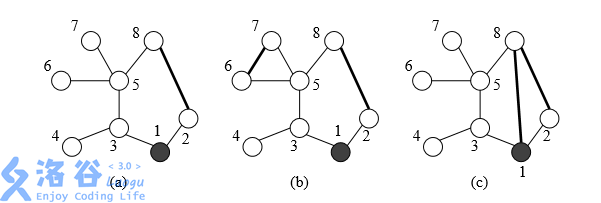
在(a)中,新建了一条道路,总的距离是 11。在(b)中,新建了两条道路,总 的巡逻距离是 10。在(c)中,新建了两条道路,但由于巡警车要经过每条新道路 正好一次,总的距离变为了 15。 试编写一个程序,读取村庄间道路的信息和需要新建的道路数,计算出最佳 的新建道路的方案使得总的巡逻距离最小,并输出这个最小的巡逻距离。
输入输出格式
输入格式:
第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行,每行两个整数 a, b, 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。
输出格式:
输出一个整数,表示新建了 K 条道路后能达到的最小巡逻距离。
输入输出样例
输入样例#1: 复制
8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6
输出样例#1: 复制
11
输入样例#2: 复制
8 2
1 2
3 1
3 4
5 3
7 5
8 5
5 6
输出样例#2: 复制
10
输入样例#3: 复制
5 2
1 2
2 3
3 4
4 5
输出样例#3: 复制
6
说明
10%的数据中,n ≤ 1000, K = 1;
30%的数据中,K = 1;
80%的数据中,每个村庄相邻的村庄数不超过 25;
90%的数据中,每个村庄相邻的村庄数不超过 150; 100%的数据中,3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。
题解
这是一颗树。
我们加一条边,就等于一个环上的边只需要走一次,其他要走两次。
k==1,我们加到直径。
k==2,我们又要多一个环。这个环可能与直径形成的环重合,那么重合的部分就要走两次。把树的直径取反,取反就等于走两遍。因为答案是2*(n-1)-直径1+1-直径2+1,让第二次的利益最大化。
顺带一句:有负边的直径要dp求。
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=2000001;
struct node{
int to,v,nex;
}e[N<<1];
int head[N],num,dis[N];
int x[N],y[N],vis[N],ff[N];
int s,t,n,k,maxn1,maxn2;
int f[N],flag[N];
int read(){
int x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
void add(int from,int to,int v){
num++;
e[num].to=to;
e[num].v=v;
e[num].nex=head[from];
head[from]=num;
}
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nex){
int v=e[i].to;if(v==fa)continue;ff[v]=u;
dis[v]=dis[u]+e[i].v;dfs(v,u);
}
}
void dp(int x){
flag[x]=1;
for(int i=head[x];i;i=e[i].nex){
int v=e[i].to;if(flag[v])continue;
dp(v);maxn2=max(maxn2,f[x]+f[v]+e[i].v);
f[x]=max(f[x],f[v]+e[i].v);
}
}
int main(){
n=read();k=read();
for(int i=1;i<n;i++){
x[i]=read(),y[i]=read();
add(x[i],y[i],1);add(y[i],x[i],1);
}
dfs(1,0);for(int i=1;i<=n;i++)
{if(dis[i]>maxn1)maxn1=dis[i],s=i;ff[i]=dis[i]=0;}
dfs(s,0);maxn1=0;
for(int i=1;i<=n;i++)
{if(dis[i]>maxn1)maxn1=dis[i],t=i;dis[i]=0;}
if(k==1){printf("%d\n",2*(n-1)-maxn1+1);return 0;}
int now=t;memset(e,0,sizeof(e));
memset(head,0,sizeof(head));num=0;
while(now){vis[now]=1;now=ff[now];}
for(int i=1;i<n;i++)
if(vis[x[i]]&&vis[y[i]])
add(x[i],y[i],-1),add(y[i],x[i],-1);
else add(x[i],y[i],1),add(y[i],x[i],1);
memset(ff,0,sizeof(ff));s=0;
dp(1);
printf("%d\n",2*(n-1)-maxn1+1-maxn2+1);
return 0;
}


