[WC2011]最大XOR和路径(线性基)
P4151 [WC2011]最大XOR和路径
题目描述
XOR(异或)是一种二元逻辑运算,其运算结果当且仅当两个输入的布尔值不相等时才为真,否则为假。 XOR 运算的真值表如下( 1 表示真, 0 表示假):
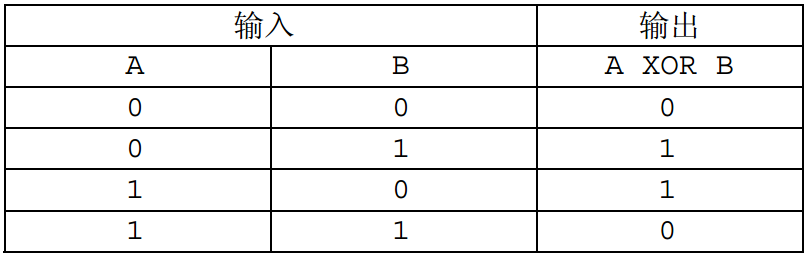
而两个非负整数的 XOR 是指将它们表示成二进制数,再在对应的二进制位进行 XOR 运算。
譬如 12 XOR 9 的计算过程如下:
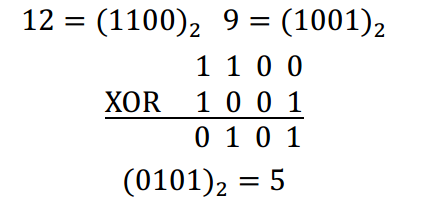
故 12 XOR 9 = 5 。
容易验证, XOR 运算满足交换律与结合律,故计算若干个数的 XOR 时,不同的计算顺序不会对运算结果造成影响。从而,可以定义 KK 个非负整数 \(A_1\),\(A_2\) ,\(……\) , \(A_{K-1}\),\(A_K\)的 XOR 和为
\(A_1\) XOR \(A_2\) XOR …… XOR \(A_{K-1}\) XOR \(A_K\)
考虑一个边权为非负整数的无向连通图,节点编号为 1 到 N ,试求出一条从 1 号节点到 N 号节点的路径,使得路径上经过的边的权值的 XOR 和最大。
路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算 XOR 和时也要被计算相应多的次数,具体见样例。
输入输出格式
输入格式:
输入文件 xor.in 的第一行包含两个整数 \(N\) 和 \(M\) , 表示该无向图中点的数目与边的数目。
接下来 M 行描述 M 条边,每行三个整数 \(S_i\) , \(T_i\) , \(D_i\) , 表示 \(S_i\) 与 \(T_i\) 之间存在一条权值为 \(D_i\) 的无向边。
图中可能有重边或自环。
输出格式:
输出文件 xor.out 仅包含一个整数,表示最大的 XOR 和(十进制结果)。
输入输出样例
输入样例#1: 复制
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
输出样例#1: 复制
6
说明
【样例说明】
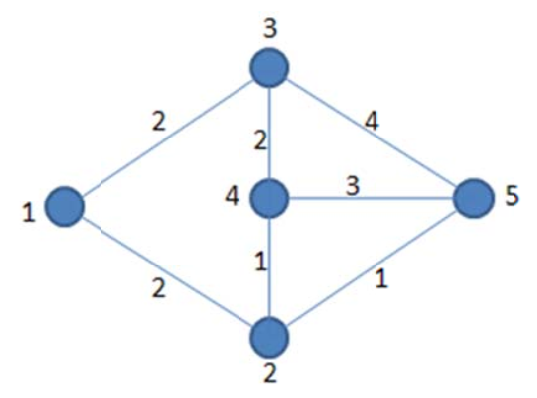
如图,路径 \(1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 5\)对应的XOR和为
2 XOR 1 XOR 2 XOR 4 XOR 1 XOR 1 XOR 3=6
当然,一条边数更少的路径 \(1 \rightarrow 3 \rightarrow 5\) 对应的XOR和也是 2 XOR 4 = 6 。
【数据规模】
对于 \(20 \%\) 的数据, \(N \leq 100\) , \(M \leq 1000\) , \(D_i\) \(\leq\) \(10^{4}\) ;
对于 \(50 \%\) 的数据, \(N \leq 1000\) , \(M \leq 10000\) , \(D_i\) \(\leq\) \(10^{18}\) ;
对于 \(70 \%\) 的数据, \(N \leq 5000\) , \(M\) \(\leq\) \(50000\) , \(D_i\) \(\leq\) \(10^{18}\) ;
对于 \(100 \%\) 的数据, \(N \leq 50000\) , \(M \leq 100000\) , \(D_i \leq 10^{18}\) 。
题解
怎么说呢。有这样一条定理
(不知道这个之前的我根本不会做这道题)
- 任意一条 \(1\) 到 \(n\) 的路径的异或和,都可以由任意一条 \(1\) 到 \(n\) 路径的异或和与图中的一些环的异或和来组合得到。
为什么?
如果我们走一条路径的话,如果路径上存在一个环,那么这个环的总异或值就可以下放到线性基。因为把这个环走两遍就等于没走这个环,同样我如果是由一条路径到的这个环,沿原路返回,那等于那条路径没走,只走了环。
在这种条件下,我们可以考虑把环储存为一个线性基的元素。因为这个元素是可选和可不选的。
那么为什么是任意的简单路径呢?
因为 \(1\) 到 \(N\) 的简单路径是必须要走的。这显然。
然后如果有多条 \(1\) 到 \(N\) 的路径,那么这显然也构成一个环,也是可以抵消异或的任意一条其他的路径的是吧。
然后这个题目就好做了咕咕咕。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#define ll long long
using namespace std;
ll dis[50001],sum[101],b[101];
ll n,m,vis[50001];
int head[100001],num;
struct node{
int next,to;
ll v;
}e[100001<<1];
ll read()
{
ll x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
void add(int from,int to,ll v){
num++;
e[num].to=to;
e[num].v=v;
e[num].next=head[from];
head[from]=num;
}
void update(ll x){
for(int i=60;i>=0;i--){
if(sum[i]&x){
if(b[i])x^=b[i];
else {
b[i]=x;
break;
}
}
}
}
void dfs(int x){
vis[x]=1;
for(int i=head[x];i;i=e[i].next){
int v=e[i].to;
if(vis[v])update(dis[v]^e[i].v^dis[x]);
else dis[v]=dis[x]^e[i].v,dfs(v);
}
}
ll query(ll x){
ll ans=x;
for(int i=60;i>=0;i--){
if((ans^b[i])>ans)ans^=b[i];
}
return ans;
}
int main()
{
n=read();m=read();
sum[0]=1;for(int i=1;i<=60;i++)sum[i]=sum[i-1]*2;
for(int i=1;i<=m;i++){
ll x=read(),y=read(),z=read();
add(x,y,z);add(y,x,z);
}
dfs(1);
printf("%lld",query(dis[n]));
return 0;
}


