[luogu] P2787 语文1（chin1）- 理理思维(分块)

P2787 语文1（chin1）- 理理思维

题目背景

蒟蒻HansBug在语文考场上，挠了无数次的头，可脑子里还是一片空白。

题目描述

考试开始了，可是蒟蒻HansBug脑中还是一片空白。哦不！准确的说是乱七八糟的。现在首要任务就是帮蒟蒻HansBug理理思维。假设HansBug的思维是一长串字符串（字符串中包含且仅包含26个字母），现在的你，有一张神奇的药方，上面依次包含了三种操作：

1. 获取第x到第y个字符中字母k出现了多少次

2. 将第x到第y个字符全部赋值为字母k

3. 将第x到第y个字符按照A-Z的顺序排序

你欣喜若狂之时，可是他脑细胞和RP已经因为之前过度紧张消耗殆尽，眼看试卷最后还有一篇800字的作文呢，所以这个关键的任务就交给你啦！

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示HansBug的思维所包含的字母个数和药方上操作个数。

第二行包含一个长度为N的字符串，表示HansBug的思维。

第3-M+2行每行包含一条操作，三种操作格式如下：

1. 操作1： 1 xi yi ki 表示将第xi到第yi个字符中ki出现的次数输出

2. 操作2： 2 xi yi ki 表示将第xi到第yi个字符全部替换为ki

3. 操作3： 3 xi yi 表示将第xi到第yi个字符按照A-Z的顺序排序

输出格式：

输出为若干行，每行包含一个整数，依次为所有操作1所得的结果。

输入输出样例

输入样例#1： 复制

10 5
ABCDABCDCD
1 1 3 A
3 1 5
1 1 3 A
2 1 2 B
1 2 3 B

输出样例#1： 复制

1
2
2

说明

样例说明：

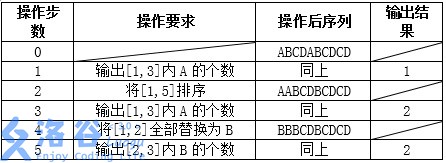
数据规模：

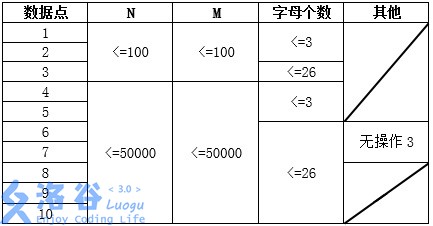
此题目中大小写不敏感。

题解

是道傻逼题。
顺便AC700祭。
作死去写分块。
发现只有第三个操作比较玄学。
第三个操作其实你可以这么想
先把这段的每个字母总数用操作一提出来，
一段一段按照第二操作覆盖就好。
这个时候还有一个问题
原数组怎么处理。
当然是打标记.jpg
这怎么会有紫题woc

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#define freopen Epiphyllum_thief
using namespace std;
const int N=2e5;
int l[1001],r[1001],sum[1001][51];
int n,m,ch[N],num,addx[1001];
int bl[N];
char s[N];

int read(){
	int x=0,w=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*w;
}

void build(){
	for(int i=1;i<=num;i++)
	l[i]=(i-1)*num+1,r[i]=i*num;r[num]=n;
	for(int i=1;i<=num;i++){
		for(int j=l[i];j<=r[i];j++){
			sum[i][ch[j]]++;bl[j]=i;
		}
	}
}

void update(int x,int y,int tmp){
	if(bl[x]==bl[y]){
		if(addx[bl[x]])
		for(int i=l[bl[x]];i<=r[bl[y]];i++)
		ch[i]=addx[bl[x]];	addx[bl[x]]=0;
		for(int i=x;i<=y;i++)
		sum[bl[x]][ch[i]]--,sum[bl[x]][tmp]++,ch[i]=tmp;
		return ;
	}
	if(addx[bl[x]]){
		for(int i=l[bl[x]];i<=r[bl[x]];i++)ch[i]=addx[bl[x]];
		addx[bl[x]]=0;
	}
	for(int i=x;i<=r[bl[x]];i++)
	sum[bl[x]][ch[i]]--,sum[bl[x]][tmp]++,ch[i]=tmp;
	for(int i=bl[x]+1;i<=bl[y]-1;i++)
	memset(sum[i],0,sizeof(sum[i])),sum[i][tmp]=num,addx[i]=tmp;
	if(addx[bl[y]]){
		for(int i=l[bl[y]];i<=r[bl[y]];i++)ch[i]=addx[bl[y]];
		addx[bl[y]]=0;
	}
	for(int i=l[bl[y]];i<=y;i++)
	sum[bl[y]][ch[i]]--,sum[bl[y]][tmp]++,ch[i]=tmp;
}

int query(int x,int y,int tmp){
	int ans=0;
	if(bl[x]==bl[y]){
		if(addx[bl[x]])
		for(int i=l[bl[x]];i<=r[bl[x]];i++)
		ch[i]=addx[bl[x]]; addx[bl[x]]=0;
		for(int i=x;i<=y;i++)if(ch[i]==tmp)ans++;
		return ans;
	}
	if(addx[bl[x]]){
		for(int i=l[bl[x]];i<=r[bl[x]];i++)ch[i]=addx[bl[x]];
		addx[bl[x]]=0;
	}
	for(int i=x;i<=r[bl[x]];i++)
	ans+=(ch[i]==tmp);
	for(int i=bl[x]+1;i<=bl[y]-1;i++)ans+=sum[i][tmp];
	if(addx[bl[y]]){
		for(int i=l[bl[y]];i<=r[bl[y]];i++)ch[i]=addx[bl[y]];
		addx[bl[y]]=0;
	}
	for(int i=l[bl[y]];i<=y;i++)
	ans+=(ch[i]==tmp);
	return ans;
}

void exchange(int x,int y){
	int tot[27];
	for(int i=1;i<=26;i++)tot[i]=query(x,y,i);
	int h=x,t=y;
	for(int i=1;i<=26;i++){
		if(!tot[i])continue;
		update(h,h+tot[i]-1,i);
		h+=tot[i];
	}
}

int main(){
	Epiphyllum_thief("data.in","r",stdin);
	Epiphyllum_thief("ans.out","w",stdout);
	n=read();m=read();
	num=sqrt(n);if(num*num<n)num++;
	scanf("%s",s+1);
	for(int i=1;i<=n;i++){
		if(s[i]>='A'&&s[i]<='Z')ch[i]=s[i]-'A'+1;
		else ch[i]=s[i]-'a'+1;
	}build();
	while(m--){
		int opt=read();
		if(opt==1){
			char ss[10];
			int x=read(),y=read(),tmp;
			scanf("%s",ss);
			if(ss[0]>='A'&&ss[0]<='Z')tmp=ss[0]-'A'+1;
			else tmp=ss[0]-'a'+1;
			printf("%d\n",query(x,y,tmp));
		}
		if(opt==2){
			int x=read(),y=read(),tmp;
			char ss[10];
			scanf("%s",ss);
			if(ss[0]>='A'&&ss[0]<='Z')tmp=ss[0]-'A'+1;
			else tmp=ss[0]-'a'+1;
			update(x,y,tmp);
		}
		if(opt==3){
			int x=read(),y=read();
			exchange(x,y);
		}
	}return 0;
}