计算机组成原理(2)——数据的表示与运算
二、数据的表示与运算
数据如何表示,运算器如何运算,算的过程如何用电路和硬件来实现。
运算器
考纲要求
1.十、二、八、十六进制数及其相互转换。真值和机器数之间的关系以及BCD码、字符与字符串编码、效验码。
(重点)数据的表示原码、反码、补码、移码以及他们之间的关联与区别。
2.定点数的表示,定点数位移运算、原码定点数加/减运算、补码定点数的加减运算、定点数乘/除运算、溢出概念和判别方法。
3.浮点数的表示(浮点数的表示范围和IEEE754标准)和浮点数的加/减运算。
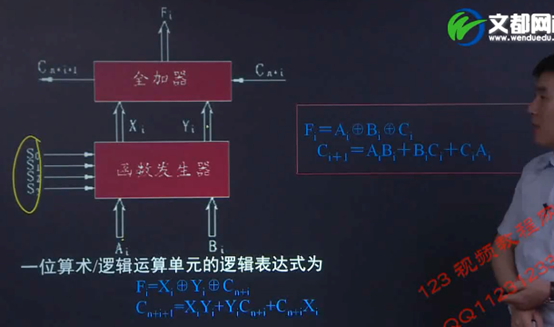
4.串行加法器和并行加法器、算术逻辑单元ALU的功能和结构。
定点数的表示
定点表示:约定机器中所有数据的小数点位置固定不变。由于约定在固定位置,小数点就不再使用记号“.”来表示。
通常将放到数值位最后面或者最前面,这样的数据表示成纯整数或纯小数。
1 无符号数的表示
用全部二进制代码表示表示数字,没有符号位。
8位二进制无符号数的范围
( 00000000~11111111) 0~2^8-1 (0~255)共256个数

问:为啥是2^8-1?
答:
1111 1111
最低位是 最高位是
1*2^0 ~ 1*2^7
s8 = 1*(1-2^8)/(1-2)
= 2^8-1
或者可以理解为加一位是1 1111 1111 是1*2^8 -1。
2. 有符号数的表示方法
定点数 x= x0 x1 x2 … xn 在机中表示如下(x0为符号位,0代表正号,1代表负号)

对于小数的表示:
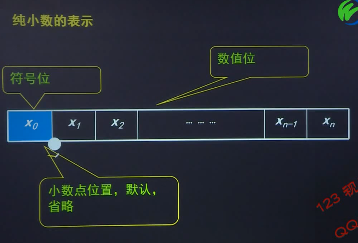
小数点位置默认省略掉。
纯小数的表示范围
(x0 x1 x2 … xn 数值位各位均为0时绝对值最小;数值位各位均为1时绝对值最大)
即这些数为: -0.11……1 <= x <= +0.11……1
|n个1| |n个1|
上结论:
0<= | x | <= 1-2^-n
-(1-2^-n) <= | x | <= 1-2^-n
结论是怎么得到的呢?
答:
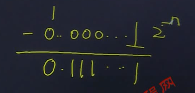
用八位二进制
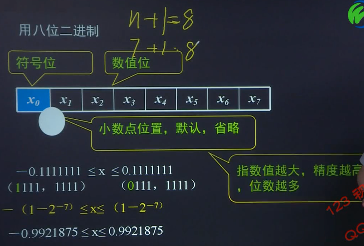
2.纯整数的表示
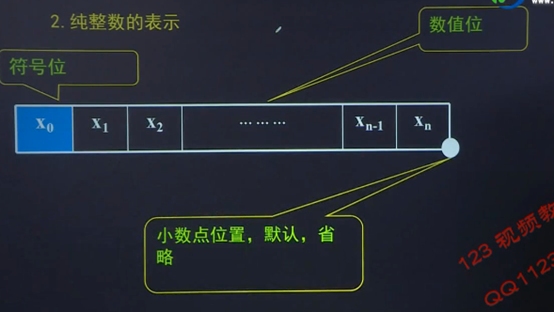
纯整数的表示范围为
(x0 x1 x2 … xn 数值位各位均为0时 绝对值最小;数值位各位均为1时绝对值最大)
结论:
-(2^n-1) <= x <= 2^n -1 (1后面n个0)
0 <= |x| <=2^n-1
即 -11……1 <= x <= + 11……1
比如说32位二进制数,符号位占了一位 数值位占了31位,

问:
机器字长为32位,定点表示时,数符1位,尾数31位。
则:定点整数表示时,
最大正数值 = _________2^31 - 1______________, (011……1)
最小负数值 = ________-2^31 - 1______________。 (11……1)
定点小数表示时,
最大正数值 =__________1 – 2^-31____________, (01……1)
最小负数值 =________-(1 – 2^-31)___________。 (11……1)
十进制加法器可由BCD码(二-十进制码)来设计,它可以在二进制加法器的基础上加上适当的”校正”逻辑来实现,该校正逻辑可将二进制的”和”改编成所要求的十进制格式。
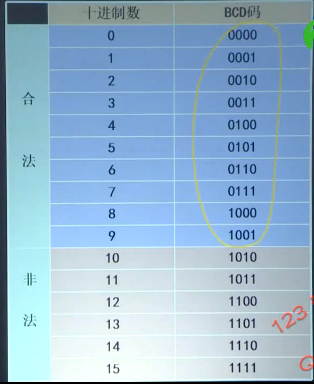
为了便于计算机的运算,必须对二进制的定点数进行合适的编码。
下面讲定点数的机器码表示:
- 原码表示法
原码就是数值的真值(绝对值)前面加上一个绝对值(正数0、负数1)。
若定点小数的原码形式为x0 x1 x2 … xn ,则原码表示的定义是
[x]原 = 0 + |x| = x (1 > x >= 0)
1 + |x| = 1-x (0 >= x >-1)
式中[x]原式机器数,x是真值
例如, x = + 0.1001,则 [x]原 = 0.1001
x = - 0.1001,则 [x]原 = 1.1001
对于0,原码机器中往往有”+0”、”-0”之分,故有两种形式:
[+0]原 = 0.000…0
[-0]原 = 1.000…0
一个n+1位(包括数值位和符号位)定点小数原码的表示范围是
-0.111…11 ~ +0.111…11
| n位 | | n位 |
-( 1 – 2^-n) <= x <= 1-2^n
若 定点整数 的原码形式为 x0 x1 x2 … xn, 则原码表示的定义是
[x]原 = 0 + | x | = x 2^n > x >=0
2^n + | x | = 2^n-x 0 >= x > -2^n
n+1位定点整数原码的表示范围是
-111…11 ~ + 111… 11
| n位 | | n位 |
-(2^n – 1) <= 2^n -1
对于0,原码机器中往往有”+0”、”-0”之分,故有两种形式:
[+0]原 = 0000…0
[-0]原 = 1000…0
n+1位定点整数原码的表示范围
-(2^n - 1) <= x <= 2^n -1
思考: n+1位定点整数原码能表示多少个数?有几个编码?
例如:1个字节8位,2^8 = 256
1位符号位,7位数值位,-127~+127 255个 因为0占了两个编码
(1) x和-x的原码转换
将[x]原的符号位(左端第一位)取反,既可得到[-x]原。
(2) 原码中0的表示不唯一。
纯小数: [+0]原 = 0.00…0, [-0]原 = 1.00…0
纯整数: [+0]原 = 00…0, [-0]原 = 100…0
(3) 若原码字长位n,总共有2^n个编码,但对应的真值只有2^n-1个。
因为[0]原占用了两个编码,因此原码表示范围较小(2^n个编码只能表示2^n-1个真值)。注意与补码的不同。
(4) 若原码字长位n,总共有2^n个编码,但对应的真值只有2^n个。
因为[0]原占用了两个编码,因此原码表示的范围较小(2^n个编码只能表示2^n-1个真值)。注意与后面补码的差异。
(5) 负数原码形式上大于正数的原码:
对于定点小数,当x>0时 0<[x]原<1;
当x<0 时 1<[x]原<2。
对于定点正数,当x>0时, x<[x]原<2^n-1;
当x<0 时, 2^n-1<[x]原<2^n。
(6) 原码的移位规则:
符号位不变,数值部分左移或右移,移出的空位填”0”。(左移一位相当于乘以2,右移一位相当于除以2)

优点:原码简单易懂,与真值转换容易,实现乘除法方便。
(乘除法数值位由两束的绝对值相乘/除得到,符号位由两束的符号位异或即可);
不足:1.原码中0的表示由两种,给使用带来了不便。
2.原码表示的加减法运算复杂,这是因为:当两数相加时如果时同号则数值相加,如果是异号,则进行减法。
2.补码表示法
举例1:假设现在的标准时间位4点正;而有一只表已经7点了,为了校准时间,可以采用两种方法:
将时针退7-4 = 3格;
将时针向后拨9格,7+9(mod 12) = 4。
这两种方法都能校准到4点。
减3和加9是等价的,即9是(-3)对12的
-3 = +9(mod12)
7-3和7+9(mod 12)等价,原因就是表指针超过12时,将12自动丢掉,最后得到16-12=4。从这里可以得到一个启示,就是负数用补码表示时可以把减法转换为加法。
7-3和7+9(mod 12) 等价,9称为-3对12的补码即:

补码的定义就是(mod+真值)
[X]补 = M + X(Mod M)
正数的补数等于本身。
负数的补码等于模与该数绝对值之差。


补码的性质:
(1) 几个特殊数值的补码表示:
0的补码表示



补码的表示范围比原码范围大
纯小数补码比原码多表示一个-1
纯整数补码比原码多表示一个-2^n
这个多表示的数来自于-0,将-0表示为上面的两个数。
所以,补码的表示范围:

8位正数/1位是符号位 7位是数值位
原码 -127~+127 255个数
补码 -128~+127之间 256个数
(3)补码和原码的关系
对于正数直接取其二进制数的表示构成补码。
即 若x>=0,[x]原=[x]补。
若 x<0 符号位不变,各位求反后最低位+1。
注意:补码中特殊数-1(纯小数)和-2^n(纯整数)的表示,在原码中没有对应表示。
(4)[x]补 和 [-x]补 的关系
·已知[x]补,将[x]补的各位(含符号位)取反,然后在最低位上加1,即得到[-x]补。反之亦然。
(5)补码的算数移位规则:
补码的左移(乘2):符号位不变,数值部分左移,最低位移出的空位填0;
补码的右移(除2):符号位不变,数值部分右移,最高位移除的空位填符号位。

(6)负数补码形式上大于正数的补码:
与原码类似
(7)补码的位扩展
例如将字节(8位二进制)表示的补码扩展位16位二进制表示的补码。
定点小数:在最低位用0扩展。
定点整数:在最高位用符号位扩展。
常用求补码的方法(与定义求补码比较):
- 若x>=0 则[x]补=x,符号位为0
若x<0 则将x绝对值的各位取反,然后再最低位上加1,符号位求1,即得到[x]补
- 若x>=0 数值位不变,符号位为0.
若x<0,数值位从最低位开始,对遇到的0和第一个1取其原来的代码,对第一个以后开始直至最高为均按位取反,符号位为1

3.反码表示法
二进制的各位数码0变为1,1变为0.
反码本身就是一个求补码的中间环节。
反码的主要作用就是求补码
对 定点小数,反码表示的定义为
[x]反 = x (1 > x >= 0) (mod(2-2^-n))
(2-2^-n) + x (0 >= x > -1)
其中n代表数的位数。
反码实质上是一种特殊的补码,其特殊支出在于反码的模比补码的模小一个最低位上的1。
对于0,有[+0]反和[-0]反之分
[+0]反 = 0.00…0
[-0]反 = 1.11…1
对于定点整数,反码表示的定义为
[x]反 = x 2^n > x >= 0
(2^n-1 – 1 ) + x 0 >= x > -2^n
反码的特点:
1) 在反码表示中,用符号位x0表示正负,形式与原码表示相同,0为正,1为负
2) 反码中,0 有两种表示形式
纯小数: [+0]反 = 0.00…0 [-0]反=1.11…1
3) 反码的表示范围与原码相同。注意,纯小数的反码不能表示为-1,纯整数的反码不能表示为-2^n
4.移码表示法
补码表示很难直接判断其真值大小。
浮点数的阶码是用移码来表示的。
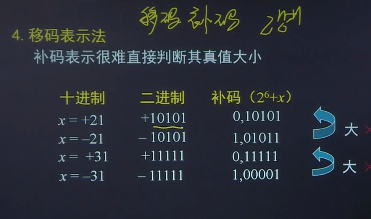
人的直觉会觉得后面的比前面的大,然而并不是这样,也并没有什么卵用。

移码
模的指数比补码少1.
2^n+1次方
2^n次方
移码通常用于表示浮点数的阶码。由于阶码是个n位的正数,假定定点整数移码形式位x0,x1,x2..xn时,
对定点整数,移码的传统定义是n位数值真值加上一个固定常数2^n
[x]移 = 2^n + x 2^n > x >= -2^n
对定点小数,移码的传统定义是真值加上一个固定常数1
[x]移 = 1+x +1 > x >= -1
若阶码数值部分为7位,以x表示真值,则
[x]移 = 2^7 + x = 128 + x 128 > x >= -128
例如,当正数 x = +1010101时,
[x]移 = 2^7 + 1010101
= 1,0000000 + 1010101
= 1,1010101;
当负数 x = -1010101时,
[x]移 = 2^7 + x = 2^7 – 1010101
= 10000000 – 1010101
= 0,0101011
移码中的逗号不是小数点,而是表示左边一位是符号位。
移码中符号位x0表示的规律与原码、补码、反码相反(0表示负1表示正)
(1)移码的几何性质
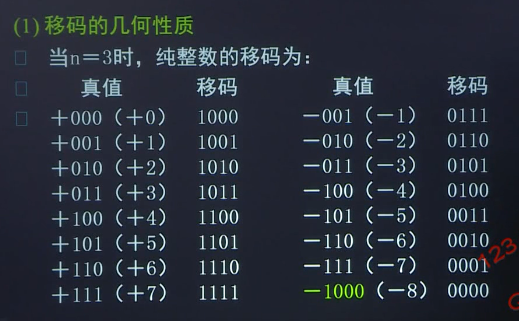
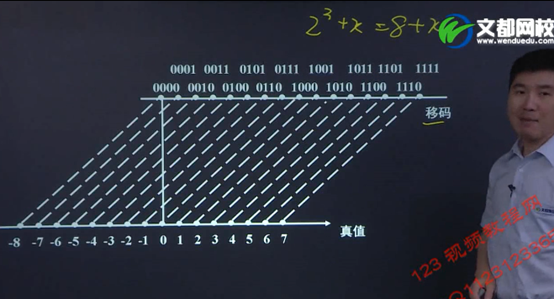
移码表示的实质是把真值映像到一个正数域,因此移码的大小可以直观的反应真值的大小。
不管整数还是负数,用移码表示时,可以按无符号数比较大小。
(1) 移码中”0”的表示
移码中”0”的表示是唯一的
[+0]移 = [-0]移 = 2^n+- 0 … 0 = 10…0 (纯整数)
移码的表数范围与补码一致。
纯整数移码表示的最小数可以表示到-2^n
(2) 移码与补码的关系
x>=0 时,[x]补=x,[x]移=2^n+x [x]移 = [x]补 + 2^n
x< 0 时, [x]补 = 2^(n+1) + x , [x]移 = 2^n + x , [x]移 = 2^n + [x]补 – 2^n+1
= [x]补 – 2^n
x = + 1011010
[x]补 = 01011010
[x]移 = 2^n+x = 2^7+1011010 = 11011010
(3) 移码的符号位:
0表示负数,1表示正数,和原码、反码、补码不同。
(4) 移码与真值的线性关系:
移码的顺序和真值完全一致,因此移码在表示阶码时可以方便的进行大小的比较,其结果与真值一致。

答:是32位机器,所以int类型是32位,y为短整形16位,
z = x + y
加减运算一定是补码运算
127 = 01111111 真值
è 0000,0000,0000,0000,0000,0000,0111,1111 = 0000007FH
-9 = 11001
-> 10111 -> 1111,1111,1111,0111 = FFF7H
127+(9)= 118 = 01110110

8位
1个符号位 7个数值位
表示范围是-128~+127

答案选B。
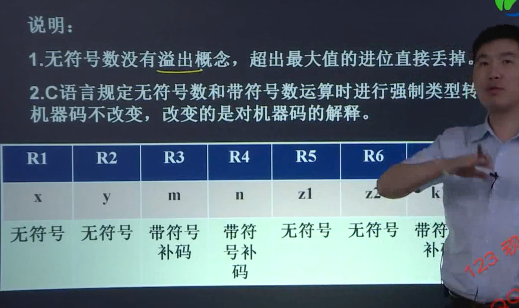
效验码
元件故障\噪声干扰等各种因素常常导致计算机在处理信息过程中出现错误。为了
防止错误,可将信号采用专门的逻辑线路进行编码以检测错误,甚至校正错误。通常的方法是,在每个字上添加一些校验位,用来确定字中出现错误的位置。
- 奇偶校验码
组成奇偶校验码的基本方法:在n位有效信息位上增加一个二进制校验位,构成一个n+1位奇偶校验码。
奇校验:使n+1位的奇偶校验码中的1的个数为奇数。
偶校验:使n+1位的奇偶校验码中的1的个数为偶数。
B.海明校验码
海明校验实质上是一种多重奇偶校验。它将有效信息按某种规律分成若干组,每组安排一个校验位作奇偶测试,就能提供多位检错信息,以指出最大可能是哪位出错,从而将其纠正。

2.2.2 定点数的运算
定点加法减法运算
补码加法
负数用补码表示后,可以和正数一样来处理。
当需要减去一个x时可以用加上x对应的负数的补码[-x]补来代替。
这样,运算器里只需要一个加法器就可以了,不必为了负数的加法运算,再配一个减法器。
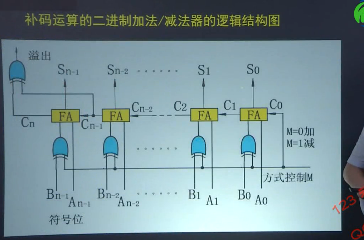
补码运算的基本规则:
- 运算的各个操作数均补码表示,运算结果仍是补码。
- 符号位与数值位一样参加运算。
- 求和求差直接加
- 补码是对确定的模而言,若运算结果超过了模,则将模自动丢掉。
2.2.23 溢出概念与检测方法

两个正数相加,结果大于机器所能表示的最大正数,称为上溢,而两个负数相加,结果小于机器所能表示的最小负数,称为下溢。
为了判断”溢出”是否发生,可采用两种检测的方法。第一种方法是采用双符号位法。
双符号位法又称变形补码,符号位又两位用”00”表示正,“11“表示负。

*了解
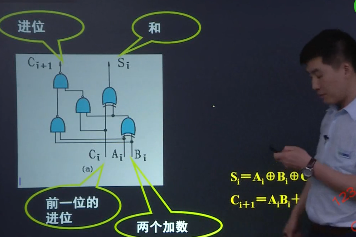
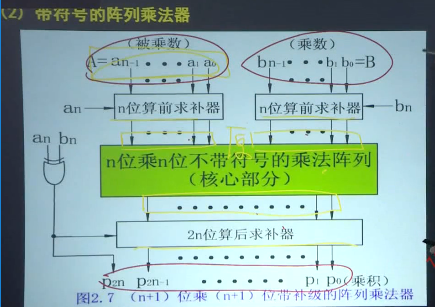
2.2 定点乘法运算
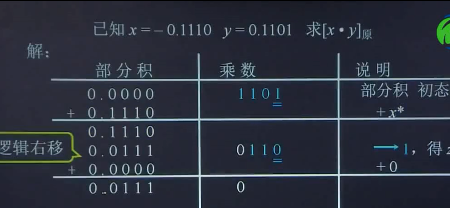
2.2.1 原码一位乘法
1.分析笔算乘法
A=-0.1101 B = 0.1011
0.1101
X 0.1011
_____________
1101
1101
0000
1101
0.10001111
乘积的符号心算求得
符号位单独处理
乘数的某一位决定是否加被乘数
4个积一起相加
乘积的位数扩大一倍
乘法改进
A*B = A* 0.1011 = A*(0.1+0.00+0.001+0.0001)
= 0.1*A + 0.00*A + 0.001*A + 0.0001*A
= 0.1{A+0.1[0*A+0.1*(A+0.1*A)]}
乘->移+加
[乘积] 0

小结
乘法 运算可用 加和移位实现
n = 4, 加4次,移4次
由成熟的末位决定被乘数是否与原部分积相加,然后à1位形成新的部分积,同时乘数->1位(末位移丢), 空出高位存放部分积的低位。
被乘数只与部分积的高位相加
硬件: 3个寄存器,具有移位功能。
1 个全加器


2.4 定点除法运算
2.4.1 原码除法运算原理


机器的运算过程和人不同,人会心算,一看就知道够不够减。
但机器却不会心算,必须先作减法。
若余数位正,才知道够减;若余数位负,才知道不够减。
不够减时必须恢复原来的余数,以便再继续往下运算。这种方法称为恢复余数法。
要回复原来的余数,只要当前的余数
恢复余数法

余数为正 商1
余数为负 商0,恢复余数
由于要恢复余数,使除法进行过程的步数不固定,因此控制比较复杂。












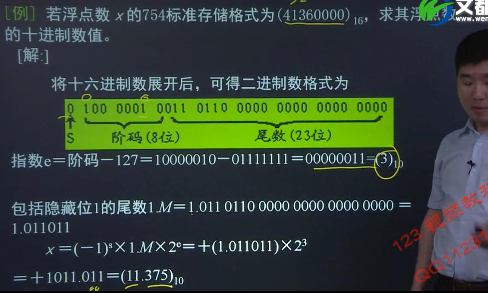
2.浮点数的表示方法










骚操作


2.6.1 浮点加法、减法运算


(3)尾数求和运算
(4)结果规格化




2.5算数逻辑单元ALU
2.5.1多功能算数/逻辑运算单元(ALU)
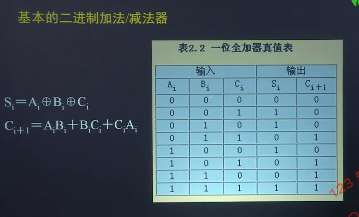
由一位全加器(FA)构成的行波进位加法器,它可以实现加法运算和减法运算。
但是这种加法/减法器存在两个问题:
一是由于串行进位,它的运算时间很长。
假如加法器由n位全加器构成,每一位的进位延迟时间为20ns,那么最坏情况下,进位信号从最低位传递到最高为而最后输出稳定,至少需要nX20ns这在高速计算中显然是不利的