数据结构——第五章 树与二叉树

 

树是一对多的结构

 

结点：树的小圆圈

度：结点有多少个分叉

叶子结点：结点的度为0

双亲：parent

孩子：child 

 

二叉树：树的度不超过2

 

满二叉树：每一层都是满的

 

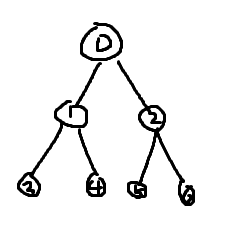
完全二叉树：除了最后一层都是满的，最后一层左边都是齐全连续的。

 

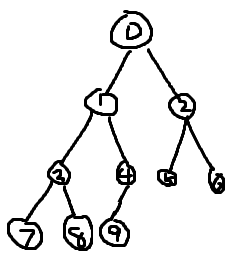
性质1：对一颗二叉树，第i层最多有2的i-1次方个

性质2：对一颗二叉树，最多有2的i次方-1个

性质3：n0=n2+1 n0+n1+n2=n（n0——结点度为0的个数，n2——结点度为2的个数）

性质4：具有n个结点的完全二叉树深度为 math.floor(log2为底n的对数)

 

性质5：将二叉树从左向右依次存放到数组中，左孩子是2*i，右孩子是2*i+1

 

二叉树的顺序存储

使用顺序表，同时，使用性质5进行存储，这样可能会造成一些空的空间。

 

二叉树的链式存储

二叉链表

 

二叉树的遍历

先序 中序 后序（左-》右）

逆先序 逆中序 逆后序（右-》左）

使用递归，

先序遍历DLR：根->左->右...

·先序中序，或 后序中序 可以唯一确定一颗二叉树

·二叉树的二叉链表结构中，有n+1个指针域未被利用

 

线索二叉树 

 

二叉树链式存储中会造成空闲指针，所以引出了线索二叉树

如果没有Lchild或Rchild，就指向前驱和后继

分别可以分为，先序，中序，后续遍历的线索二叉树

前序线索树中，前驱指向（中->左->右） 从这里找 （如果是左就找中，如果是右就找左，如果是中就找右）

。。。。类似都是这样

 

哈夫曼树

路径长度:是指一个结点到另外一个结点之间分支的数目。

 带权路径长度是指每个分支上有权值，一个结点到另外一个结点所有路径权值总和。

树的路径长度则为从根结点出发到每一个叶结点的路径长度总和。树的带权路径长度则是从根结点出发到每一个叶节点的带权路径长度总和，叫做WPL。

哈夫曼树 主要用途是实现数据压缩，编码。

 

给定了字母及各个字母出现的频度，可以根据哈夫曼树确定高效率的传输编码。

 

比如2，4，5，7

第一步从小到大排着，取出两个最小的合成一个

重复这个步骤..

假设a出现2次、b出现7次、c出现4次、d出现5次

给左边的都置0 右边的置1 则可以得出他们对应的编码

 

树，森林和二叉树的转换

 树的存储结构:

树的双亲表示法:

一组连续的存储单元，每个节点有两个域，一个是data域，另一个是parent域，用来存放双亲的位置(指针)。树的孩子表示法，树的双亲孩子表示法...

 

树和二叉树的转换，

1.连线

相邻的兄弟间连线。

2.抹线

抹掉双亲与除左孩子外其他孩子间的连线。

3.旋转

只需将树做适当的旋转。

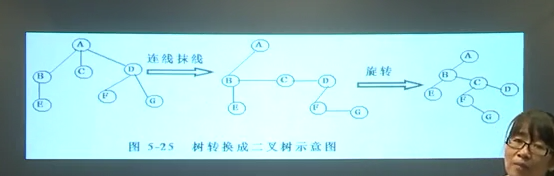
（这张图好像错了..）

森林转换成二叉树，

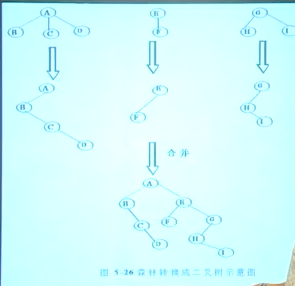
先转换成二叉树，然后依次插在根节点的右边。

 

 

二叉树还原成 树或森林

(1)右链断开

将二叉树根节点的右链及右链的右链等全部断开，得到若干颗无右子树的二叉树.

(2)二叉树还原成树

将(1)中得到的每一颗二叉树都还原成树(与树转换成二叉树的步骤相反)

 

树和森林的遍历

在树和森林中，一个结点可能有两颗以上的子树，所以不宜讨论他们的中序遍历，即树和森林只有中序遍历和后序遍历

1.先序遍历

[树的先序遍历]若树非空，则先访问根节点，然后依次先序遍历各子树

[森林的先序遍历]若森林非空，则先访问森林中第一棵树的结点，再先序遍历各子树，

2.后序遍历

[树的后序遍历]若树非空，则依次后序遍历各子树，最后访问根结点。

[森林的后序遍历]按顺序后序遍历森林中的每一次棵树。