数据结构——第三章 栈 第四章 队列

栈，先入后出

 

1.栈的进出问题（题目一般只说入栈顺序，而没说啥时候出来）

 

2.逆波兰式（栈的后缀表示，从中缀转后缀）

 

例：

（a+b）*3 +2

运算符在两个操作数中间，为中缀表达式

 

因为电脑太笨，所以需要将中缀表达式转换成后缀表达式，利用栈进行计算。

 

算法：

如何将中缀表达式转换成后缀表达式？

1.按执行的先后顺序，给表达式全部加上括号

2.把所有运算符移到右括号的后面

3.把所有的括号删除

 

例： a/b^c+d*e-a*c

 

1.这个式子需要这样计算 （（（a/（b^c））+（d*e） ）-（a*c））

2.（（（a（bc）^）/（de）* ）+（ac）*）-

3. abc^/de*+ac*-

 

对于计算机：

1。读取表达式exp的一个单词x

2。若x是操作数，则原样输出。否则执行3：

3。x是运算符。若x是） 则将栈中元素输出  直到遇到（为止。将（从栈中删除，执行4

4。x不是），循环比较栈顶元素和x的优先级，若不小于，则栈顶元素出栈输出

5。x进栈

6。若表达式已读完，则执行1，否则执行7

7。将栈中元素依次输出，直至栈空。

 

例如：8-（3+5）*（5-6/2）

 

 

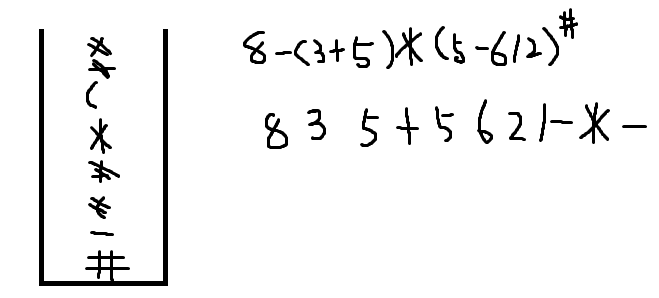
队列，先进先出。

对于顺序队列，入队的新元素是在线性表的最后，时间复杂度O(1)，

出队时需要将后续的所有元素向前移动，时间复杂度时O(n)，那么如何使它的时间复杂度降低到O(1)呢？

　　定义front使其始终代表头的下标

出队时将对头元素返回，且front++

　　定义rear使其始终代表队尾下一个元素的下标

入队时将新元素插入，且rear++

 

链队列。

*循环队列。

 

1.队空 Q.front == Q.rear

2.队满 Q.front == Q.rear 

          (Q.rear+1)%Max = Q.front

 

假满

当元素被插入到数组中下标最大的位置上之后，队列的空间就用尽了，尽管此时数组的低端还有空闲空间，这种现象叫做假溢出。
将存储队列的数组头尾相接，形成循环队列。队头、队尾指针加1时用语言的取模(余数)运算实现。
队头指针进1: Q.front = (Q.front+1) % MAXQSIZE;
队尾指针进1: Q.rear = (Q.rear+1) %MAXQSIZE;

 

3.入队 Q.rear = (Q.rear + 1)%Max

4.出队 Q.front = (Q.front + 1)%Max

5.循环队列    最多元素个数

    Max空间    Max-1

6.   实际元素   Q.front Q.rear

方1  画图