尾递归

尾递归:

  

 

https://en.wikipedia.org/wiki/Tail_call

'Tail calls can be implemented without adding a new stack frame to the call stack'

如果语言对尾递归的情况做过优化，那么在调用时候可以不增加栈帧，达到优化的目的。

 

拿斐波那契额数列举例：

 

 

 

 

 

 

在最后return的一行，可能会进入递归计算，导致调用栈占用空间太大

如果return后面直接跟的是这个函数本身，我们称它为尾递归 

 

 

 

 

==========================================================

例子1：

 

 

使用尾递归，

 

关键点：

1. helper function  （go）

2.  accumulator(parameter)

 

 

 

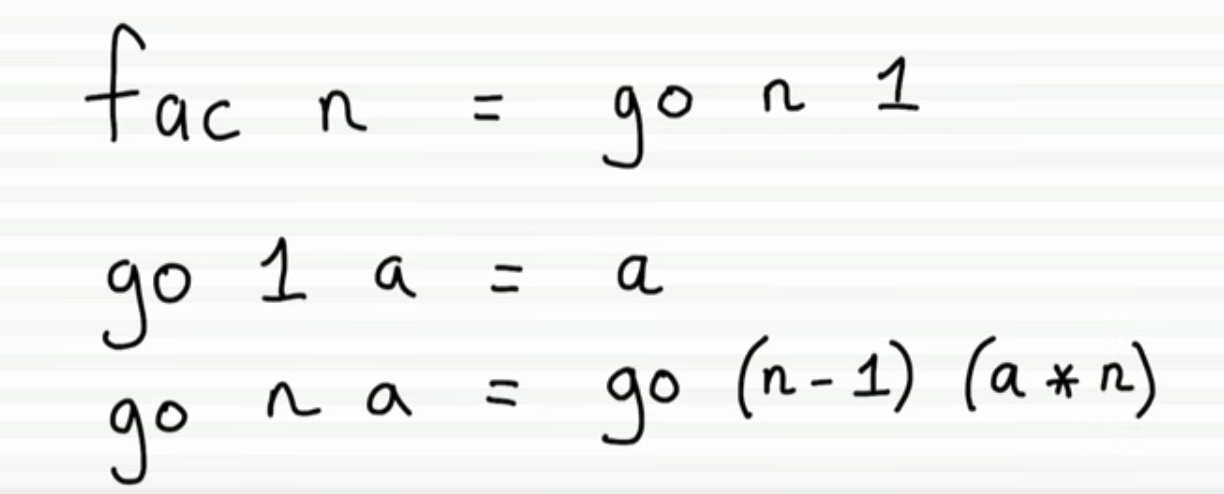
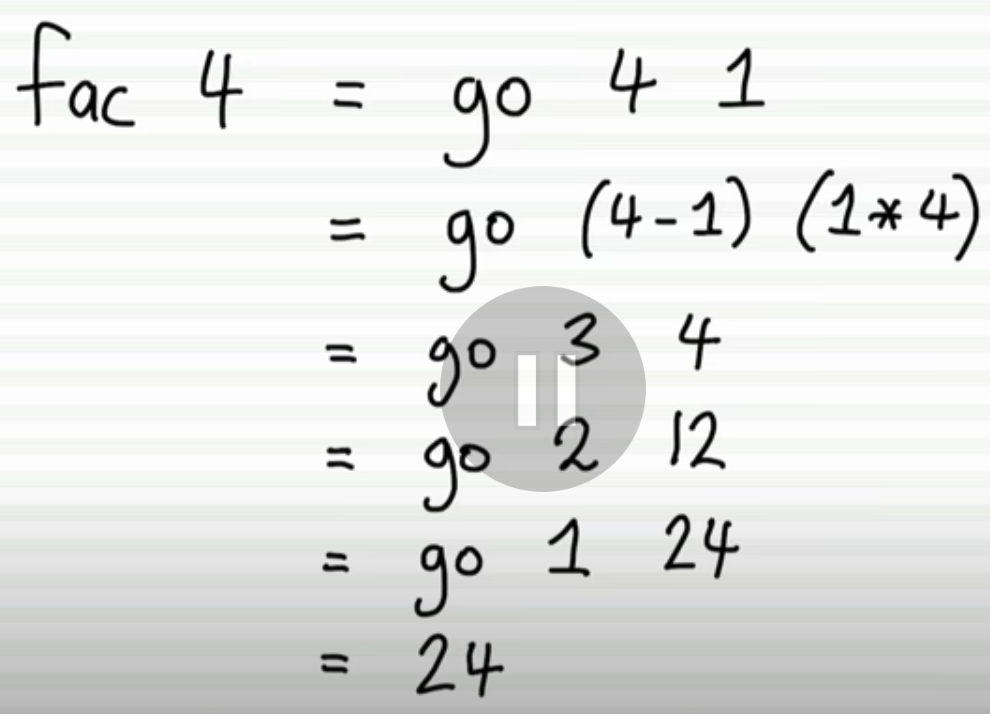
可以看到 accumulator从1开始逐渐增加，最终得到结果

 

 

例子2：斐波那契

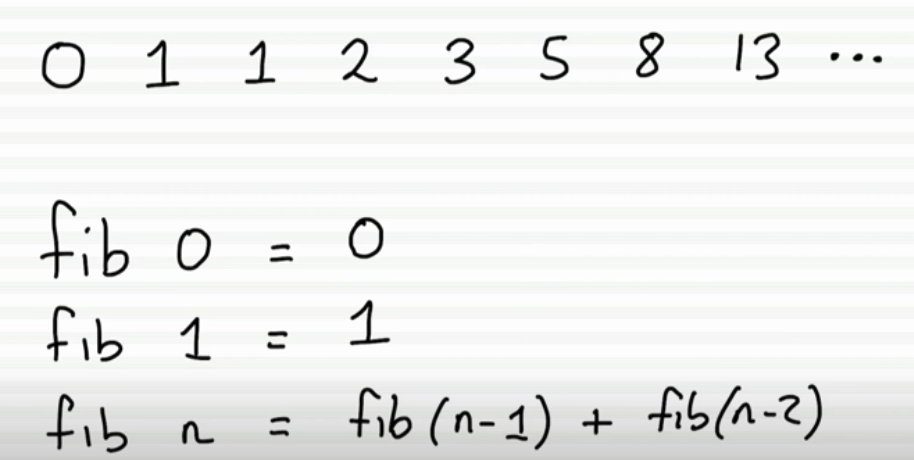
效率太低 

 

 

 

 

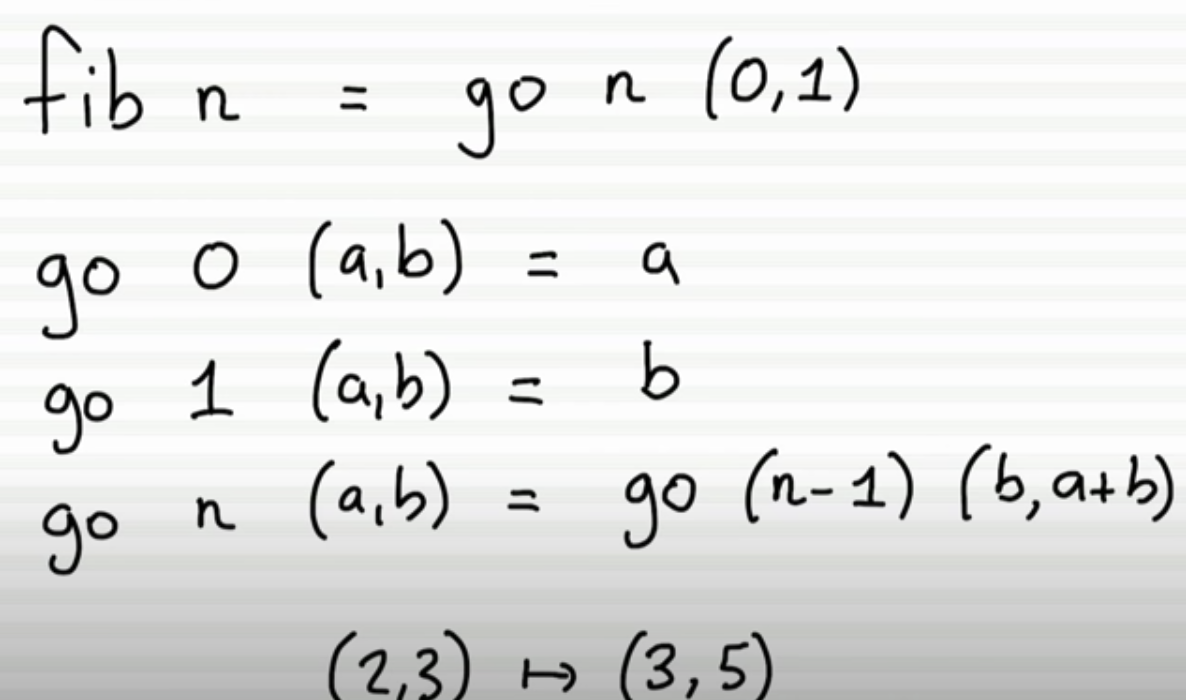
使用helper function go：

我们想象一个窗口，这个窗口一开始是0，1，然后是 1，1，然后1，2，然后是2，3，我们可以利用这个窗口作为parameter来进操作。

 go n (0,1)是最基础的，

然后我们用

go 0 (a,b) 的值其实就是a

go 1 (a,b) 的值其实就是b

go n (a,b)的值 其实是 go n-1 (b,a+b)   （注意，这里在利用窗口操作）

 

 

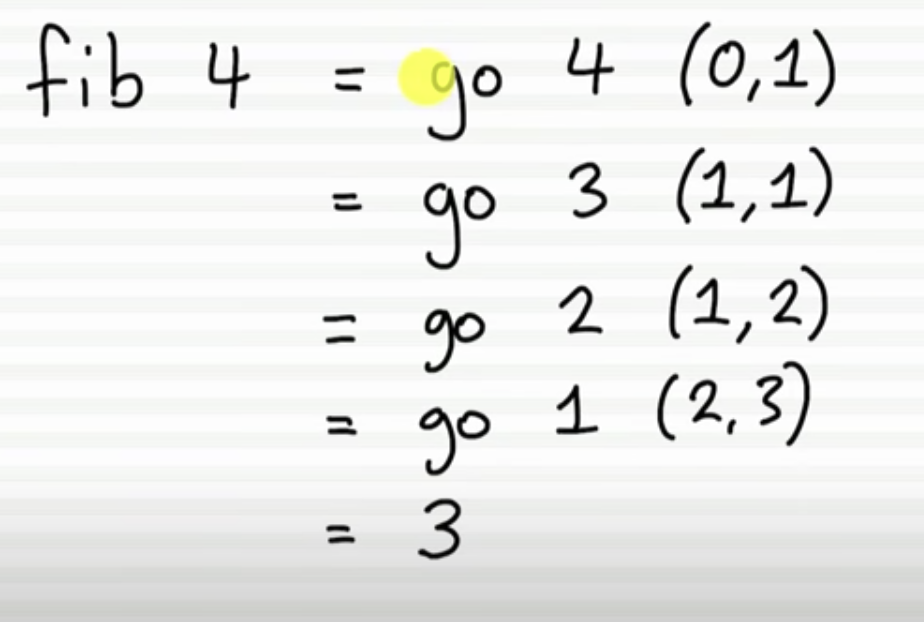
计算fib4

 

go 4 (0,1)

=go 3 (1,1)

=go 2 (1,2)

=go 1 (2,3)

= 3

 

 总结一下共性：

1.首先找到一个helper函数，这个函数的n是递减，可以向前推导

2.在参数parameter中使用accumulator进行操作，对于例子二斐波那契，使用两个参数观察这个窗口

 

 

资料： https://www.youtube.com/watch?v=_JtPhF8MshA