数据结构(3) 第三天 栈的应用:就近匹配/中缀表达式转后缀表达式 、树/二叉树的概念、二叉树的递归与非递归遍历(DLR LDR LRD)、递归求叶子节点数目/二叉树高度/二叉树拷贝和释放
01 上节课回顾
受限的线性表
栈和队列的链式存储其实就是链表 但是不能任意操作 所以叫受限的线性表
02 栈的应用_就近匹配
案例1就近匹配:

#include <stdio.h> int main() { int a[4][4];int(*p)[4];p = a[0]; return 0;}

扫描字符串 如果碰到左括号 直接入栈
如果碰到右括号 从栈顶弹出括号,判断是否是左括号, 如果是 匹配成功
如果不是 匹配失败
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include "linkstack.h"
// 算法:就近匹配
// 定义结构体 (企业链表
// 结构体内保存了字符地址和index位置
typedef str4uct MYCHAR{
// 企业链表
LinkNode node;
// 保存字符地址
char * pAddress;
// index位置
int index;
} MyChar;
// 判断是否是左括号
int IsLeft(char c) {
return c == '(';
}
// 判断是否是右括号
int isRight(char c) {
return c == ')';
}
// 在堆上创建myChar结构体 将字符的地址和index传给myChar结构体
MyChar* CreatemyChar(char *p,int index) {
// 创建mychar结构体
MyChar * mychar = (MyChar *)malloc(sizeof(MyChar));
// 字符串p的地址传给pAddress
mychar->pAddress = p;
// index传给index
mychar->index = index;
// 返回mychar结构体
return mychar;
}
void ShowError(char * str, int pos)
{
// 公有两种错误: 1 左括号没有匹配的右括号 2 右括号没有匹配的左括号
printf("%s\n",str);
for (int i = 0; i < pos;i++) {
printf(" ");
}
// 用↑指向有问题的字符
printf("↑");
}
int main(void)
{
// 就近匹配案例
char * str = "1+2+6(dsf)dfsflp((sdfs)";
//char * str = "1212())))";
// 创建栈容器
LinkStack * stack = Init_LinkStack();
// p指向str 此时*p 就是str1
char * p = str;
// index初始化为0
int index = 0;
// 循环 如果没到结尾 就一直循环, *p代表第1个字符 如果没到\0, 没到字符串的结尾
while (*p != '\0') {
// 如果遇到左括号 左括号这个字符进栈 栈里只存放( 这一种括号
if (IsLeft(*p)) {
// 如果是左括号 就创建MYCHAR结构体并推入到栈内
Push_LinkStack(stack, (LinkNode *)CreatemyChar(p,index));
}
// 如果遇到右括号 从栈顶弹出元素 本次把和这个右括号对称的左括号弹出
if (isRight(*p)) {
// (()
// 如果栈里面有内容
if (Size_LinkStack(stack) > 0) {
// 构造mychar结构体指向 栈顶元素
MyChar* mychar = (MyChar *)Top_LinkStack(stack);
// 如果是左括号
if (IsLeft(*(mychar->pAddress))) {
// 出栈
Pop_LinkStack(stack);
free(mychar);
}
}
else {
// 如果遇到了右括号 但是栈里没有内容 说明已经出错了
// 如果栈里没有内容 输出:右括号没有匹配的左括号
printf("右括号没有匹配的左括号\n");
// 显示错误信息
// 此时的index指向的是哪里?
ShowError(str, index);
break;
}
}
// 地址++
p++;
// index++
index++;
}
// 如果栈里有内容
while (Size_LinkStack(stack) > 0) {
// 构造mychar结构体指向栈顶元素
MyChar * mychar = (MyChar *)Top_LinkStack(stack);
printf(" 左括号没有匹配的右括号:\n");
ShowError(str, mychar->index);
// 出栈
Pop_LinkStack(stack);
free(mychar);
}
printf("\n");
system("pause");
return 0;
}
03 栈的应用_中缀表达式转后缀表达式
案例2:

int ret = a + b + c *(5/3)
char * ret = “a + b + c * (5/3)“

中缀转后缀表达式算法:

优先级顺序: x* > +- > ()
举例:
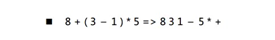
04 栈的应用_中缀表达式转后缀表达式实现1
05 栈的应用_中缀表达式转后缀表达式实现2
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include "linkstack.h"
// 中缀表达式 转 后缀表达式
// 判断是否是数字
int IsNumber(char c) {
return c >= '0' && c <= '9';
}
// 判断是不是左括号
int IsLeft(char c) {
return c == '(';
}
// 判断是不是右括号
int IsRight(char c) {
return c == ')';
}
// 判断是不是运算符号
int IsOperator(char c) {
return c == '+' || c == '-' || c == '*' || c == '/';
}
// 返回运算符号优先级
int GetPriority( char c) {
if (c == '*' || c == '/')
{
return 2;
}
if (c == '+' || c == '-') {
return 1;
}
// 什么都没有返回0
return 0;
}
// 定义Mychar结构体
// 包含一个小结点和 字符位置(企业链表
typedef struct MYCHAR {
LinkNode node;
char *p;
} Mychar;
// 创建MyChar
Mychar * CreateMyChar(char *p) {
// 在堆空间 开辟MyChar结构体大小
Mychar * mychar = (Mychar *)malloc(sizeof(Mychar));
// mychar的p 是p
mychar->p = p;
// 返回结构体
return mychar;
}
// 数字操作 遇到数字就输出
void NumberOperate(char * p) {
printf("%c", *p);
}
// 左括号的操作
void LeftOperate(LinkStack * stack,char *p) {
// 遇到左括号 把左括号推入到栈中
Push_LinkStack(stack, (LinkNode *)CreateMyChar(p));
}
// 右括号操作 遇到右括号 将栈顶元素弹出并输出 直至遇到左括号
void RightOperate(LinkStack * stack)
{
// 当栈中还有元素的时候 循环,
while (Size_LinkStack(stack) > 0) {
// 取到栈顶的元素
Mychar* mychar = (Mychar *)Top_LinkStack(stack);
// 如果是这个栈顶符号是左括号
if (IsLeft(*(mychar->p))) {
// 左括号出栈 (#不输出左括号
Pop_LinkStack(stack);
// break跳出循环
break;
}
// 输出字符
printf("%c", *(mychar->p));
// 弹出栈
Pop_LinkStack(stack);
// 释放内存
free(mychar);
}
}
// 运算符号的操作
void OperatorOperate(LinkStack *stack, char * p)
{
// 先取出栈顶符号
Mychar * mychar = (Mychar *)Top_LinkStack(stack);
// 如果栈顶是空的 就把运算符号压栈
if (mychar == NULL) {
Push_LinkStack(stack, (LinkNode *)CreateMyChar(p));
return;
}
// 如果栈顶优先级低当前字符的优先级 直接入栈 (栈里还可能没有元素
if (GetPriority(*(mychar->p)) > GetPriority(Top_LinkStack(p))) {
Push_LinkStack(stack, (LinkNode *)CreateMyChar(p));
return;
}
else {
// 如果栈顶优先级不低(大于等于当前字符优先级) 把栈顶符号弹出并输出 之后进栈
// 如果栈里有元素
while (Size_LinkStack(stack) > 0) {
// 取到栈顶元素
Mychar* mychar2 = (Mychar*)Top_LinkStack(stack);
// 如果栈顶元素优先级低于当前字符优先级 直接入栈 这个字符处理完成了 跳出循环
if (GetPriority(*(mychar2->p)) < GetPriority(*p)) {
// 入栈
Push_LinkStack(stack, (LinkNode*)CreateMyChar(p));
// 跳出循环
break;
}
// 输出 这个高优先级的字符
printf("%c",*(mychar2->p));
// 弹出栈元素
Pop_LinkStack(stack);
// 释放
free(mychar2);
}
}
}
int main(void)
{
// 中缀表达式
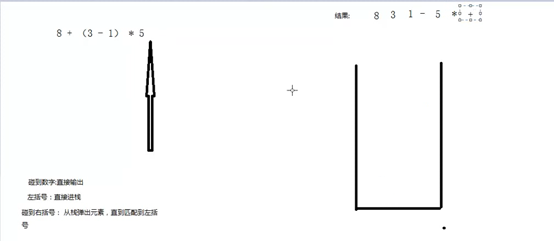
char *str = "8+(3-1)*5"; // 结果应该是8 3 1 - 5 * +
// 定义*p 指向str
char *p = str;
// 初始化栈容器
LinkStack * stack = Init_LinkStack();
// 没到结尾的时候 就一直遍历循环
while ( *p != '\0')
{
// 如果是数字
if (IsNumber(*p)) {
// 对数字进行操作(输出数字
NumberOperate(p);
}
// 如果左括号 直接进栈
if (IsLeft(*p)) {
// 对左括号进行操作 进栈
LeftOperate(stack,p);
}
// 如果右括号 将栈顶符号弹出 直到匹配到
if (IsRight(*p)) {
// 对右符号操作 将栈顶符号弹出
RightOperate(stack);
}
// 如果是运算符号
if (IsOperator(*p)) {
OperatorOperate(stack, p);
}
// p++
p++;
}
// 如果栈内还有元素 输出
while (Size_LinkStack(stack) > 0) {
Mychar * mychar = (Mychar *)Top_LinkStack(stack);
printf("%c", *(mychar->p));
Pop_LinkStack(stack);
free(mychar);
}
system("pause");
return 0;
}
06 栈的应用_后缀表达式求解
8 3 1 – 5 * +


#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "linkstack.h"
// 判断是否是数字
int IsNumber(char c)
{
return c >= '0' && c <= '9';
}
// 定义MyNum结构体
typedef struct MYNUM {
LinkNode node;
// int类型
int val;
} MyNum;
// 计算函数 传入 左操作数 右操作数 和 运算符号
int Calculate(int left, int right ,char c) {
int ret = 0;
switch (c)
{
case '+':
ret = left + right;
break;
case '-':
ret = left - right;
break;
case '*':
ret = left * right;
break;
case '/':
ret = left / right;
break;
default:
break;
}
// 计算并返回ret
return ret;
}
int main(void)
{
// 后缀表达式
char *str = "831-5*+";
char * p = str;
// 创建栈
LinkStack* stack = Init_LinkStack();
// 到字符结束前
while (*p != '\0') {
// 如果是数字 直接入栈
if (IsNumber(*p)) {
// 在堆空间分配MyNum大小结构体
MyNum * num = (MyNum *)malloc(sizeof(MyNum));
num->val = *p - '0'; //拿到数字
// 数字直接进栈
Push_LinkStack(stack, (LinkNode *)num);
}
else {
// 先从栈中弹出右操作数
MyNum * right = (MyNum *)Top_LinkStack(stack);
// 拿到rightNum
int rightNum = right->val;
// 出栈
Pop_LinkStack(stack);
free(right);
// 从栈中弹出左操作数
MyNum * left = (MyNum *)Top_LinkStack(stack);
// 拿到leftNum
int leftNum = left->val;
// 出栈
Pop_LinkStack(stack);
free(left);
// 结果进行计算拿到ret
int ret = Calculate(leftNum, rightNum, *p);
// 在堆空间创建num结构体
MyNum * num = (MyNum *)malloc(sizeof(MyNum));
// 赋值
num->val = ret;
// 将结果入栈
Push_LinkStack(stack, (LinkNode *)num);
}
p++;
}
// 如果运算完后容器内只有一个元素
if (Size_LinkStack(stack) == 1) {
// 拿到栈顶元素
MyNum * num = (MyNum *)Top_LinkStack(stack);
// 打印运算结果
printf("运算结果是:%d\n", num->val);
// 出栈
Pop_LinkStack(stack);
// 释放内存
free(num);
}
// 释放栈
FreeSpace_LinkStack(stack);
system("pause");
return 0;
}
07 树的基本概念
树和二叉树
线性表: 第一个数据只有一个后继 没有前驱,最后一个只有前驱 没有后继,其他都有前驱和后继,结点之间一对一的关系。

树里面包含树 递归性


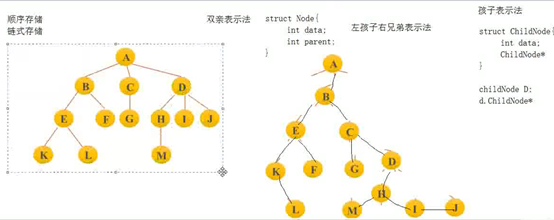
08 树的存储
线性表: 顺序存储 链式存储

树:
双亲表示法
孩子表示法
(第二个元素是一个链表将这些孩子串起来)
左孩子右兄弟表示法
(转化成了一颗二叉树
09 二叉树的基本概念

满二叉树


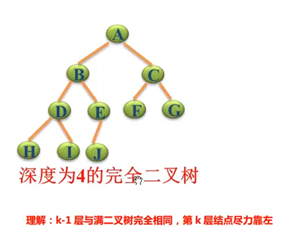
Full Tree 满二叉树
Complete tree 完全二叉树
http://web.cecs.pdx.edu/~sheard/course/Cs163/Doc/FullvsComplete.html
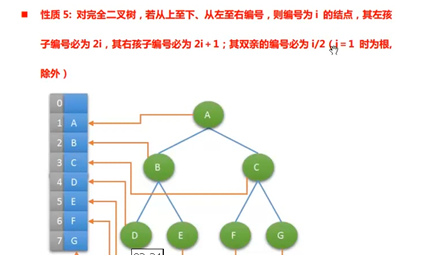
09 二叉树的基本概念
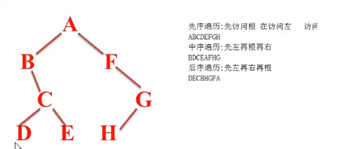
10 二叉树先序遍历_中序遍历_后序遍历


we let L, D, R stand for moving left, process(print & proess) the data, and moving right


PRE-ORDER(DLR) Traversal 前序
IN-ORDER(LDR) Traversal 中序
POST_ORDER(LRD) Traversal 后序
拿中序遍历举例:
LDR:
LDR的意思就是先访问左节点 然后打印当前结点 最后访问右节点
从A开始 A开始访问左节点是B,
看B ,先访问B的左节点没有,打印当前结点 即B 访问B的右节点C
看C,先访问C的左节点,到D
看D 先访问D的左节点 没有 然后打印当前节点 即D
打印C 访问C的右节点E
。。。。
输出 BDCEA….
11 二叉树递归遍历
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 二叉树结点
typedef struct BINARYNODE {
char ch;
struct BINARYNODE * lchild;
struct BINARYNODE * rchild;
} BinaryNode;
void CreateBinaryTree() {
// 初始化结点
BinaryNode node1 = { 'A',NULL,NULL };
BinaryNode node2 = { 'B',NULL,NULL };
BinaryNode node3 = { 'C',NULL,NULL };
BinaryNode node4 = { 'D',NULL,NULL };
BinaryNode node5 = { 'E',NULL,NULL };
BinaryNode node6 = { 'F',NULL,NULL };
BinaryNode node7 = { 'G',NULL,NULL };
BinaryNode node8 = { 'H',NULL,NULL };
// 建立结点关系
node1.lchild = &node2;
node1.rchild = &node6;
node2.rchild = &node3;
node3.lchild = &node4;
node3.rchild = &node5;
node6.rchild = &node7;
node7.lchild = &node8;
// 递归遍历
Recursion(&node1);
printf("\n");
}
// 递归遍历
void Recursion(BinaryNode * root) {
// 递归一般都把退出条件放在最开始 如果遇到推出条件就不再执行了
if (root == NULL) {
return;
}
// 先访问根节点
printf("%c", root->ch);
// 再遍历左子树
Recursion(root->lchild);
// 再遍历右子树
Recursion(root->rchild);
}
int main(void) {
CreateBinaryTree();
printf("\n");
system("pause");
return 0;
}
BFS和DFS的概念:
上面讲的前序中序后序都是指深度优先遍历

以前遇到的一道面试题
对于二叉树:
?? 深度优先 使用栈 如果右边有就入栈
?? 广度优先

补:
LDR中序遍历:

/* inOrder.js */
//**

**//
补充: LRD后序遍历

(使用两个栈)
LRD
思路:
建立两个栈
第一个栈推入根节点
如果第一个栈内有东西
{
从第一个栈中弹出元素 将元素推入第二个栈
如果这个元素有左结点 推入左结点到第一个栈
如果这个元素有右结点 推入右结点到第一个站
}
将第二个栈中元素依次输出并打印

*
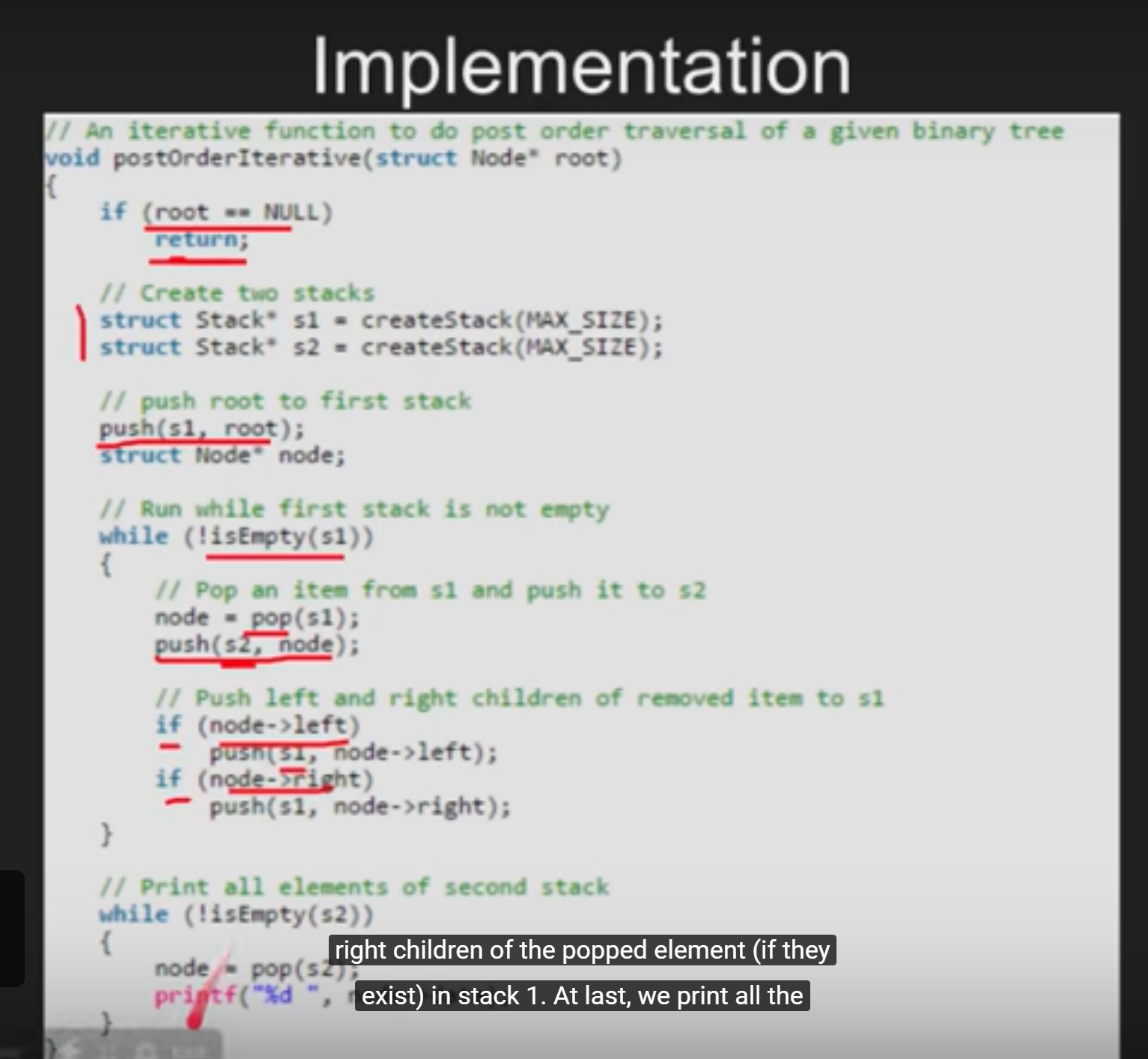
function postOrder(root)
{
let stack1,stack2
stack1.push(root)
while( stack1.size > 0 )
{
let tmpNode = stack1.pop()
stack2.push(tmpNode)
if(tmpNode>left) // left先入
stack1.push(tmpNode->left)
if(tmpNode->right)
stack1.push(tmpNode->right)
}
while( stack2.size > 0 ){
node = pop(stack2)
cout << node->data << " ";
}
}

前序中序后序都是属于深度优先遍历
广度优先遍历
12 二叉树编程实战_求叶子结点数目
叶子结点:

(度为0的结点称为叶子结点)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 二叉树结点
typedef struct BINARYNODE {
char ch;
struct BINARYNODE * lchild;
struct BINARYNODE * rchild;
} BinaryNode;
int num = 0;
// 递归计算叶子结点
void CalculateLeafNum(BinaryNode * root){
// 设置递归退出条件
if (root == NULL) {
return;
}
// 左边也没有 右边也没有 就是叶子节点
if (root->lchild == NULL && root->rchild == NULL) {
num++;
}
// 左子树叶子结点的数目
CalculateLeafNum(root->lchild);
// 右子树叶子结点的数目
CalculateLeafNum(root->rchild);
}
void CreateBinaryTree() {
// 初始化结点
BinaryNode node1 = { 'A',NULL,NULL };
BinaryNode node2 = { 'B',NULL,NULL };
BinaryNode node3 = { 'C',NULL,NULL };
BinaryNode node4 = { 'D',NULL,NULL };
BinaryNode node5 = { 'E',NULL,NULL };
BinaryNode node6 = { 'F',NULL,NULL };
BinaryNode node7 = { 'G',NULL,NULL };
BinaryNode node8 = { 'H',NULL,NULL };
// 建立结点关系
node1.lchild = &node2;
node1.rchild = &node6;
node2.rchild = &node3;
node3.lchild = &node4;
node3.rchild = &node5;
node6.rchild = &node7;
node7.lchild = &node8;
CalculateLeafNum(&node1);
printf("叶子结点的数目:%d\n",num);
}
int main(void) {
CreateBinaryTree();
printf("\n");
system("pause");
return 0;
}
13 二叉树编程实战_求二叉树的高度
递归计算二叉树高度
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 二叉树结点
typedef struct BINARYNODE {
char ch;
struct BINARYNODE * lchild;
struct BINARYNODE * rchild;
} BinaryNode;
int num = 0;
// 递归计算树的高度
int CalculateHeight(BinaryNode *root) {
int height;
int leftHeight = 0;
int rightHeight = 0;
// 如果有左子树
if (root->lchild != NULL) {
// 就计算左子树高度
leftHeight = CalculateHeight(root->lchild);
}
// 如果有右子树
if (root->rchild != NULL) {
// 就计算右子树高度
rightHeight = CalculateHeight(root->rchild);
}
// 高度是左子树高度,右子树高度中最大的 然后+1
height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
// 返回高度
return height;
}
void CreateBinaryTree() {
// 初始化结点
BinaryNode node1 = { 'A',NULL,NULL };
BinaryNode node2 = { 'B',NULL,NULL };
BinaryNode node3 = { 'C',NULL,NULL };
BinaryNode node4 = { 'D',NULL,NULL };
BinaryNode node5 = { 'E',NULL,NULL };
BinaryNode node6 = { 'F',NULL,NULL };
BinaryNode node7 = { 'G',NULL,NULL };
BinaryNode node8 = { 'H',NULL,NULL };
// 建立结点关系
node1.lchild = &node2;
node1.rchild = &node6;
node2.rchild = &node3;
node3.lchild = &node4;
node3.rchild = &node5;
node6.rchild = &node7;
node7.lchild = &node8;
int num = CalculateHeight(&node1);
printf("二叉树的高度是:%d\n",num);
}
int main(void) {
CreateBinaryTree();
printf("\n");
system("pause");
return 0;
}
14 二叉树的拷贝和释放
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 二叉树结点
typedef struct BINARYNODE {
char ch;
struct BINARYNODE * lchild;
struct BINARYNODE * rchild;
} BinaryNode;
// 遍历二叉树
void Recursion(BinaryNode * root) {
if (root == NULL) {
return;
}
printf("%c", root->ch);
// 遍历左子树
Recursion(root->lchild);
// 遍历右子树
Recursion(root->rchild);
}
// 递归拷贝二叉树
BinaryNode * CopyBinaryTree(BinaryNode * root) {
if (root == NULL) {
return NULL;
}
// 拷贝左子树
BinaryNode * lchild = CopyBinaryTree(root->lchild);
// 拷贝右子树
BinaryNode * rchild = CopyBinaryTree(root->rchild);
// 创建结点
BinaryNode * newnode = (BinaryNode *)malloc(sizeof(BinaryNode));
newnode->ch = root->ch;
newnode->lchild = lchild;
newnode->rchild = rchild;
return newnode;
}
// 递归释放二叉树内存
void FreeSpaceBinaryTree(BinaryNode* root) {
if (root == NULL) {
return;
}
// 释放左子树
FreeSpaceBinaryTree(root->lchild);
// 释放右子树
FreeSpaceBinaryTree(root->rchild);
// 释放当前结点
free(root);
}
void CreateBinaryTree() {
// 初始化结点
BinaryNode node1 = { 'A',NULL,NULL };
BinaryNode node2 = { 'B',NULL,NULL };
BinaryNode node3 = { 'C',NULL,NULL };
BinaryNode node4 = { 'D',NULL,NULL };
BinaryNode node5 = { 'E',NULL,NULL };
BinaryNode node6 = { 'F',NULL,NULL };
BinaryNode node7 = { 'G',NULL,NULL };
BinaryNode node8 = { 'H',NULL,NULL };
// 建立结点关系
node1.lchild = &node2;
node1.rchild = &node6;
node2.rchild = &node3;
node3.lchild = &node4;
node3.rchild = &node5;
node6.rchild = &node7;
node7.lchild = &node8;
BinaryNode * root = CopyBinaryTree(&node1);
Recursion(root);
FreeSpaceBinaryTree(root);
}
int main(void) {
CreateBinaryTree();
printf("\n");
system("pause");
return 0;
}




