高等数学(9) 导数与微分

 

引例1 变速直线运动的速度

 

设质点运动位置的函数为 s = f(t)

 

 

 

 

为什么叫dy/dx呢    derivative n.衍生物，导数

 

 

 

 

 

 

二、导数的概念(幂函数求导-单侧导数-切线与法线方程)

 

 

 

 

 

 

 

 

 

 

 

函数可导性与连续性关系

 

 

连续却不一定可导

 

 

注意

f(x0)‘ ≠ f(x)’ (x0)

 

 

例9:

 

 

 

 

 

连续:

可导 

 

 

===============================================================================

 

 

 

 

 

 

 

 

 

 

*左连续

*右连续

 

 

 

9-4 导数小结

 

1.导数的实质:增量比的极限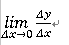

2.f’(x0) = a   ->  f+’(x0) = f-‘(x0)

3.导数的几何意义:切线的斜率

4.可导必连续,但连续不一定可导

5.判断可导性:直接用导数定义

            看左右导数是否存在且相等

 

 

9-5 函数求导法则

 

四则运算求导法则

证明:

 

三项的可以先看成是两项的

 

 

 

6 复合函数求导法则

 

 

 

 

 

 

7 常数和基本初等函数求导公式

 

 

 

例题

 

(注意可导一定连续 连续不一定可导,所以下面的解答是正确的

 

 

8 高阶导数

 

 

 

二阶导数..三阶导数..

 

 

 

 

9 高阶导数运算法则

 

 

 

 

小结

高阶导数球阀

1.逐阶求导法

2.利用归纳法

3.利用莱布尼兹公式

 

 

10.隐函数导数‘

 

 

 

 

 

 

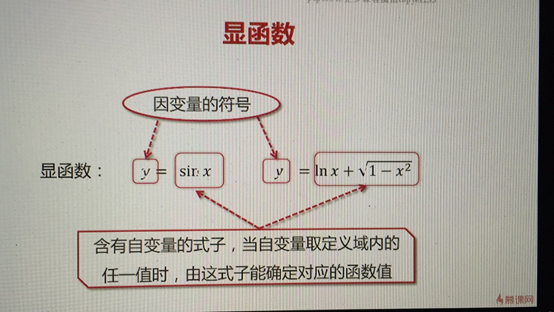
11 幂指函数求导

 

 

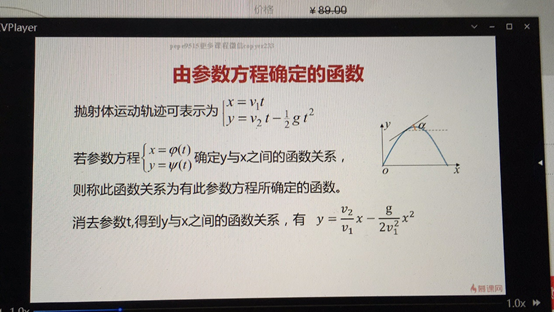
12 由参数方程确定的函数