AC自动机
背景
给出一个字典,和若干询问:多少个字典串在询问串中出现过。
即单串与多串的匹配问题。
AC自动机
AC 自动机基于 Trie,将 KMP 的 Border 概念推广到多模式串上。
AC 自动机是一种离线型数据结构,即不支持增量添加新的字符串。
AC 自动机常用于将字符串询问类的问题进行离线处理,也经常与各种 DP 结合,或是补全成 Trie 图。
border概念的推广
推广到两个串:对于两个串 S 和 T,相等的 p 长度的 S 的后缀和 T 的
前缀称为一个 border。
推广到一个字典:对于串 S 和一个字典 D,相等的 p 长度的 S 的后缀,
和任意一个字典串 T 的前缀称为一个 border。
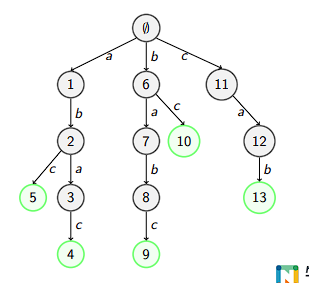
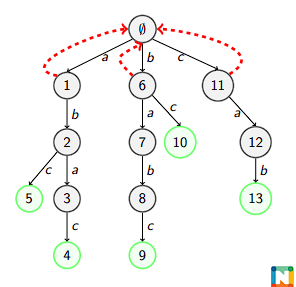
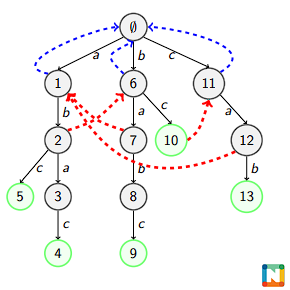
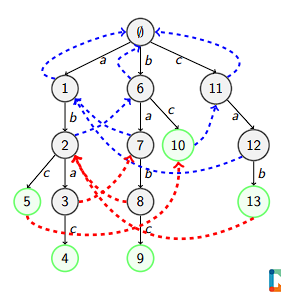
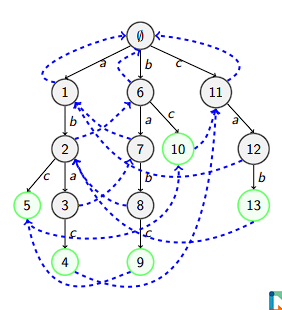
失配(Fail)指针: 对于 Trie 中的每一个节点(即某个字典串的前缀),
它与 Trie 中所有串的最大 Border 即为失配指针。
失配指针
类似与 KMP 求 Border,任意节点的 Border 长度减一,一定是父节点的
Border。因此可以通过遍历父节点的失配指针链来求解。
因此在求失配指针的时候,一定要按长度从小到大来求,即 bfs。
复杂度分析
类似于 KMP 的势能分析方法,势能总量等于 Trie 的节点总数,因此复
杂度为线性的。
模板
点击查看代码
struct ACAM{
int tot,ch[maxn][27],fail[maxn],biao[maxn];
void insert(string s){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'A';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
biao[u]=1;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
//biao[ch[u][i]]|=biao[fail[ch[u][i]]];
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
}A;
例题
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int ans[maxn],id[maxn],cnt[maxn],in[maxn];
struct ACAM{
int tot,ch[maxn][27],biao[maxn],fail[maxn];
void insert(string s,int pos){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'a';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
id[pos]=u;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
in[fail[ch[u][i]]]++;
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
void find(string s){
int u=0,lenth=s.length();
for(int i=0;i<lenth;i++){
int k=s[i]-'a';
u=ch[u][k];
int tmp=u;
while(tmp){
cnt[tmp]++;
tmp=fail[tmp];
}
}
return ;
}
void get_ans(){
queue<int>q;
for(int i=1;i<=tot;i++)if(!in[i])q.push(i);
while(!q.empty()){
int u=q.front();q.pop();
int v=fail[u];
cnt[v]+=cnt[u];
in[v]--;
if(!in[v])q.push(v);
}
return ;
}
}A;
int main(){
int n=read();
for(int i=1;i<=n;i++){
string s;cin>>s;
A.insert(s,i);
}
A.getfail();
string now;cin>>now;
A.find(now);//A.get_ans();
for(int i=1;i<=n;i++)cout<<cnt[id[i]]<<endl;
return 0;
}
2.string
题意:先输入n个字符串放在仓库中,然后m次询问,每一次询问有两种类型。类型1是在仓库中新添加一个字符串。类型2是输入一个字符串,然后问当前仓库中有多少字符串是你操作2输入的字符串的子串。
题解:
AC自动机无法在线处理这道题,考虑离线
我们首先将所有在仓库的字符串(包括初始化的n个和之后所有类型1的询问)构建AC自动机
然后构建fail树
若fail树上一个特殊点(字符串的结尾)能够被匹配到,那么这个点到根的路径上的所有特殊点都可以被匹配到
那么我们可以考虑dfs序+树状数组来处理,处理出每个特殊点到根的特殊点数:每个特殊点在它的子树内节点权值+1
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int limi,f[maxn];
int lowbit(int x){return x&(-x);}
void add(int pos,int val){
for(int i=pos;i<=limi;i+=lowbit(i))f[i]+=val;
}
int query(int pos){
int ans=0;
for(int i=pos;i;i-=lowbit(i))ans+=f[i];
return ans;
}
int id[maxn]; //记录特殊点的位置
struct ACAM{
int tot,ch[maxn][27],fail[maxn];
int top,l[maxn],r[maxn];
void init(){
top=0;
memset(l,0,sizeof(int)*(tot+1));
memset(r,0,sizeof(int)*(tot+1));
for(int i=0;i<=tot;i++)for(int j=0;j<26;j++)ch[i][j]=0;
memset(fail,0,sizeof(int)*(tot+1));
memset(f,0,sizeof(int)*(tot+10));
tot=0;
return;
}
void insert(string s,int pos){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'a';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
id[pos]=u;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
void solve(){
vector<vector<int> >G(tot+1);
for(int i=1;i<=tot;i++)G[fail[i]].pb(i);
function<void(int)> dfs=[&](int u){
l[u]=++top;
for(auto v:G[u])dfs(v);
r[u]=top;
};
dfs(0);
return ;
}
int find(string s){
int u=0,lenth=s.length(),ans=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'a';
u=ch[u][k];
ans+=query(l[u]);
}
return ans;
}
}A;
struct que{
int opt;
string s;
};
void solve(){
int n=read(),m=read();
for(int i=1;i<=n;i++){
string s;cin>>s;
A.insert(s,i);
}
vector<que>q(m+1);
for(int i=1;i<=m;i++){
q[i].opt=read();cin>>q[i].s;
if(q[i].opt==1)A.insert(q[i].s,i+n);
}
A.getfail();
A.solve();
limi=A.tot+2;
for(int i=1;i<=n;i++){
add(A.l[id[i]],1);add(A.r[id[i]]+1,-1);
}
for(int i=1;i<=m;i++){
if(q[i].opt==1){
add(A.l[id[i+n]],1);add(A.r[id[i+n]]+1,-1);
}
else printf("%d\n",A.find(q[i].s));
}
A.init();
return;
}
int main(){
int t=read();
while(t--)solve();
return 0;
}
3.[CERC2018]The ABCD Murderer

题解:

考虑如何得到最长的\(S_i\)
我们可以在求fail的时候,维护每个AC自动机上点的最长后缀长度的biao数组
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+101;
const int MOD=998244353;
const int inf=2147483647-2;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct SgT{
int tr[maxn];
void build(int k,int l,int r){
if(l==r){
tr[k]=inf;
return ;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
tr[k]=min(tr[k<<1],tr[k<<1|1]);
return ;
}
void modify(int k,int l,int r,int pos,int val){
if(pos<l || r<pos)return ;
if(l==r){
tr[k]=val;
return ;
}
int mid=(l+r)>>1;
modify(k<<1,l,mid,pos,val);modify(k<<1|1,mid+1,r,pos,val);
tr[k]=min(tr[k<<1],tr[k<<1|1]);
return ;
}
int get_minn(int k,int l,int r,int L,int R){
if(r<L || R<l)return inf;
if(L<=l && r<=R)return tr[k];
int mid=(l+r)>>1;
return min(get_minn(k<<1,l,mid,L,R),get_minn(k<<1|1,mid+1,r,L,R));
}
}T;
struct ACAM{
int tot,ch[maxn][27],fail[maxn],biao[maxn],id[maxn];
void insert(string s){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'a';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
id[u]=1;biao[u]=lenth;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
if(biao[fail[ch[u][i]]]){
//按照bfs顺序,biao[fail[ch[u][i]]一定先求出来了
biao[ch[u][i]]=max(biao[ch[u][i]],biao[fail[ch[u][i]]]);
}
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
int dp[maxn];
int find(string s){
int lenth=s.length(),u=0;
T.build(1,1,lenth);
for(int i=1;i<=lenth;i++){
int k=s[i-1]-'a';
u=ch[u][k];dp[i]=inf;
if(biao[u]){
if(i-biao[u]==0)dp[i]=1;
else dp[i]=T.get_minn(1,1,lenth,i-biao[u],i-1)+1;
}
T.modify(1,1,lenth,i,dp[i]);
}
return dp[lenth]>=inf?-1:dp[lenth];
}
}A;
int n;
string t;
int main(){
n=read();cin>>t;
for(int i=1;i<=n;i++){
string s;cin>>s;
A.insert(s);
}
A.getfail();
cout<<A.find(t)<<endl;
return 0;
}
4.[JSOI2007]文本生成器
题解:

时间复杂度为\(O(状态数*转移)\)
加强版为\(m\leq 10^4\)
考虑优化
我们可以将转移优化下,由\(O(100*26)->O(26)\)
我们可以预处理当前点转移到哪
注意某个节点是否可行,得看它的所有fail树上都是否可行
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+11;
const int MOD=10007;
const int inf=2147483647-2;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int power(int x,int y){
int ans=1;
while(y){
if(y&1)ans=ans*x%MOD;
y>>=1;x=x*x%MOD;
}
return ans;
}
struct ACAM{
int tot,ch[maxn][27],fail[maxn],biao[maxn];
void insert(string s){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'A';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
biao[u]=1;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
biao[ch[u][i]]|=biao[fail[ch[u][i]]]; //fail树上有结尾标记,当前点也是不可行的
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
int dp[2][maxn];
int get_dp(int lenth){
dp[0][0]=1;
for(int i=1;i<=lenth;i++){
for(int u=0;u<=tot;u++)dp[i&1][u]=0;
for(int u=0;u<=tot;u++)for(int k=0;k<26;k++){
if(biao[ch[u][k]])continue;
(dp[i&1][ch[u][k]]+=dp[(i-1)&1][u])%=MOD;
}
}
int ans=0;
for(int i=0;i<=tot;i++)(ans+=dp[lenth&1][i])%=MOD;
return ans;
}
}A;
int main(){
int n=read(),m=read();
for(int i=1;i<=n;i++){
string s;cin>>s;
A.insert(s);
}
A.getfail();
printf("%lld\n",((power(26,m)-A.get_dp(m))%MOD+MOD)%MOD);
return 0;
}
5.DNA Sequence
题意:

题解:
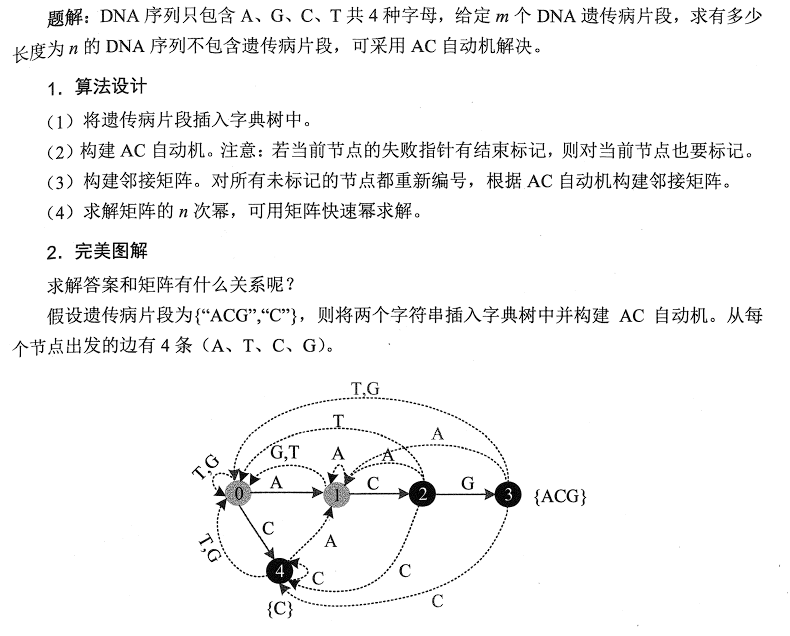


这道题跟上一道题有点类似,这道题给的串很短,要找的串很长,所以可以用矩阵优化
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<string>
#include<cmath>
#include<queue>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+11;
const int MOD=100000;
const int inf=2147483647-2;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int len;
struct Matrix{
ll a[103][103]; //矩阵大小记得修改!!!
void init(){
for(int i=0;i<len;i++){
for(int j=0;j<len;j++)a[i][j]=(i==j);
}
}
void zero(){memset(a,0,sizeof(a));}
Matrix operator*(Matrix m2){
Matrix m;m.zero();
for(int i=0;i<len;i++){
for(int j=0;j<len;j++){
for(int k=0;k<len;k++){
(m.a[i][j]+=a[i][k]*m2.a[k][j]%MOD)%=MOD;
}
}
}
return m;
}
Matrix operator^(ll y){
Matrix sum,x;sum.init();
memcpy(x.a,a,sizeof(a));
while(y){
if(y&1)sum=sum*x;
y>>=1;x=x*x;
}
return sum;
}
};
struct ACAM{
int tot,ch[maxn][4],fail[maxn],biao[maxn];
void init(){
for(int i=0;i<=tot+5;i++){
for(int j=0;j<4;j++)ch[i][j]=0;
fail[i]=0;biao[i]=0;
}
tot=0;
return ;
}
int idx(char ch){
switch(ch){
case 'A':return 0;
case 'C':return 1;
case 'T':return 2;
case 'G':return 3;
}
return 0;
}
void insert(string s){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=idx(s[i]);
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
biao[u]=1;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<4;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<4;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
biao[ch[u][i]]|=biao[fail[ch[u][i]]];
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
int solve(int lenth){
Matrix t;len=0;
vector<int>f(tot+1);
for(int u=0;u<=tot;u++){
if(biao[u])continue;
f[u]=len++;
}
for(int u=0;u<=tot;u++){
if(biao[u])continue;
for(int i=0;i<4;i++){
if(biao[ch[u][i]])continue;
t.a[f[u]][f[ch[u][i]]]++;
}
}
t=t^lenth;
int ans=0;
for(int i=0;i<len;i++)(ans+=t.a[0][i])%=MOD;
return (ans%MOD+MOD)%MOD;
}
}A;
int main(){
int m,n;
while(~scanf("%d%d",&m,&n)){
for(int i=1;i<=m;i++){
string s;cin>>s;
A.insert(s);
}
A.getfail();
cout<<A.solve(n)<<endl;
A.init();
}
return 0;
}
如果要求长度小于等于n的不包含给定串的方案数,该如何求?




6.病毒
是否存在一个无限长的不包含给定串的字符串
等价于在AC自动机上走,不走给定字符串结尾点,是否能走出一个环
直接dfs
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+11;
const int MOD=10007;
const int inf=2147483647-2;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct ACAM{
int tot,ch[maxn][27],fail[maxn],biao[maxn];
void insert(string s){
int lenth=s.length(),u=0;
for(int i=0;i<lenth;i++){
int k=s[i]-'0';
if(!ch[u][k])ch[u][k]=++tot;
u=ch[u][k];
}
biao[u]=1;
return ;
}
void getfail(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<2;i++){
if(ch[u][i]){
q.push(ch[u][i]);
fail[ch[u][i]]=ch[fail[u]][i];
biao[ch[u][i]]|=biao[fail[ch[u][i]]];
}
else ch[u][i]=ch[fail[u]][i];
}
}
return ;
}
int vis[maxn];
int dfs(int x){
if(vis[x]==1)return 1;
if(vis[x]==-1)return 0;
vis[x]=1;int now=0;
for(int i=0;i<2;i++){
if(biao[ch[x][i]])continue;
now|=dfs(ch[x][i]);
if(now)return 1;
}
vis[x]=-1;
return 0;
}
}A;
int main(){
int n=read();
for(int i=1;i<=n;i++){
string s;cin>>s;
A.insert(s);
}
A.getfail();
if(A.dfs(0))puts("TAK");
else puts("NIE");
return 0;
}

