KMP
Border
如果字符串 \(S\) 的同长度的前缀和后缀完全相同,即 \(Prefix[i] = Suffix[i]\)
则称此前缀(后缀)为一个 \(Border\)(根据语境,有时 \(Border\) 也指长度)。
特殊地,字符串本身也可以是它的 \(Border\),具体是不是根据语境判断。
周期和循环节
对于字符串 \(S\) 和正整数 \(p\),如果有 \(S[i] = S[i − p]\),对于 \(p < i ≤ |S|\) 成
立,则称 \(p\) 为字符串 \(S\) 的一个周期。
特殊地,\(p = |S|\) 一定是 \(S\) 的周期
若字符串 \(S\) 的周期 \(p\) 满足 \(p \:\: |\:\: |S|\),则称 \(p\) 为 \(S\) 的一个循环节
特殊地,\(p = |S|\) 一定是 \(S\) 的循环节
重要性质
Border vs 周期
\(p\) 是 \(S\) 的周期 ⇔ \(|S| − p\) 是 \(S\) 的 \(Border\)
证明
\(p 为 S 的周期 ⇔ S[i − p] = S[i]\)
\(q 为 S 的 Border ⇔ S[1, q] = S[|S| − q + 1, |S|] ⇔
S[1] = S[|S| − q + 1], S[2] = S[|S| − q + 2], . . . , S[q] = S[|S|]\)
\(所以|S|-q是一个周期\)
\(易得:p + q = |S|\)
因此,字符串的周期性质等价于 \(Border\) 的性质,
求周期也等价于求 \(Border\)。
警告:\(Border\) 不具有二分性。
Border 的传递性
\(S\) 的 \(Border\) 的 \(Border\) 也是 \(S\) 的 \(Border\)
求 \(S\) 的所有 \(Border\) 等价于求所有前缀的最大 \(Border\)
KMP
next数组
\(next[i]=Preffix[i]\)的非平凡(去掉字符串本身)的最大\(Border\)
\(next[1]=0\)
考虑 \(Prefix[i]\) 的所有(长度大于 \(1\) 的)\(Border\),去掉最后一个字母,就
会变成 \(Prefix[i − 1]\) 的 \(Border\)。
因此求 \(next[i]\) 的时候,可以遍历 \(Prefix[i − 1]\) 的所有 \(Border\),即
\(next[i − 1], next[next[i − 1]], . . . , 0,\)检查后一个字符是否等于 \(S[i]\)。
复杂度分析
\(考虑使用势能分析进行讨论:\)
\(如果 next[i] = next[i − 1] + 1,则势能会增加 1\)
\(否则势能会先减少到某个 next[j],然后有 next[i] = next[j] + 1,势能
也会增加 1,在寻找 next[j] 的过程中,势能会减少,每次至少减少
1。\)
\(还有一种情况,next[i] = 0,势能清空,且不会增加。\)
\(综上,势能总量为 O(N),因此整体的复杂度也是 O(N),常数为 2 左右
(很小)。空间复杂度也为 O(N)。\)
实现
void init(string s){
//s="!"+s' 使得s从[1,len]
len=s.length()-1;
t=s;
for(int i=2;i<=len;i++){
nxt[i]=nxt[i-1];
while(nxt[i] && s[i]!=s[nxt[i]+1])nxt[i]=nxt[nxt[i]];
nxt[i]+=(s[i]==s[nxt[i]+1]);
}
return ;
}
字符串匹配
struct KMP{
int len,nxt[maxn];
string t;
void init(string s){
//s="!"+s' 使得s从[1,len]
len=s.length()-1;
t=s;
for(int i=2;i<=len;i++){
nxt[i]=nxt[i-1];
while(nxt[i] && s[i]!=s[nxt[i]+1])nxt[i]=nxt[nxt[i]];
nxt[i]+=(s[i]==s[nxt[i]+1]);
}
return ;
}
vector<int> match(string s){
//查看s中字符串t的位置
int len_s=s.length();
int j=0;
vector<int>ans;
for(int i=0;i<len_s;i++){
while(j && s[i]!=t[j+1])j=nxt[j];
if(s[i]==t[j+1])j++;
if(j==len){
ans.pb(i+1-len+1);
//记录起始位置
j=nxt[j];
}
}
return ans;
}
};
例题
1.栗酱的数列

点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=2e5+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct KMP{
int len,nxt[maxn];
vector<int> t;
void init(vector<int> s){
//s="!"+s' 使得s从[1,len]
for(int i=0;i<=len;i++)nxt[i]=0;
len=s.size()-1;
t=s;
for(int i=2;i<=len;i++){
nxt[i]=nxt[i-1];
while(nxt[i] && s[i]!=s[nxt[i]+1])nxt[i]=nxt[nxt[i]];
nxt[i]+=(s[i]==s[nxt[i]+1]);
}
return ;
}
ll match(vector<int> s){
//查看s中字符串t的位置
int len_s=s.size();
int j=0;
ll ans=0;
for(int i=0;i<len_s;i++){
while(j && s[i]!=t[j+1])j=nxt[j];
if(s[i]==t[j+1])j++;
if(j==len){
ans++;
j=nxt[j];
}
}
return ans;
}
void debug(){
for(auto i:t)cout<<i<<" ";puts("");
for(int i=1;i<=len;i++)cout<<nxt[i]<<" ";puts("");
}
}P;
void solve(){
int n=read(),m=read(),k=read();
vector<int>a(n),b(m+1);
for(int i=0;i<n;i++)a[i]=read();
for(int i=1;i<=m;i++)b[i]=read();
vector<int>aa,bb;
for(int i=1;i<n;i++)aa.pb(((a[i]-a[i-1])%k+k)%k);
for(int i=1;i<=m;i++)bb.pb(((-b[i]+b[i-1])%k+k)%k);
P.init(bb);
int ans=P.match(aa);
cout<<ans<<endl;
return ;
}
int main(){
int t=read();
while(t--)solve();
return 0;
}
Border 树
对于一个字符串 \(S,n = |S|,\)它的 \(Border\) 树(也叫 \(next 树\))共有 \(n + 1\)
个节点:\(0, 1, 2, . . . , n。\)
\(0\) 是这棵有向树的根。对于其他每个点 \(1 ≤ i ≤ n\) ,父节点为 \(next[i]\) 。
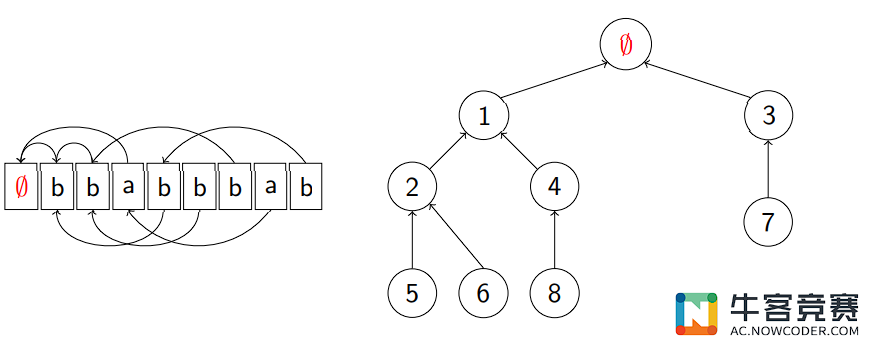
性质
- 每个前缀 \(Prefix[i]\) 的所有 \(Border\):节点 i 到根的链。
- 哪些前缀有长度为 \(x\) 的 \(Border\):\(x\) 的子树。
- 求两个前缀的公共 \(Border\) 等价于求 \(LCA\)。
例题
1.葫芦和斌斌的字符串1
运用第二个性质
查看那个长度为x的border的子树size大于等于k
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define YES {puts("YES");return;}
#define NO {puts("NO");return ;}
using namespace std;
const int maxn=5e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-8;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct KMP{
int len,nxt[maxn];
string t;
void init(string s){
//s="!"+s' 使得s从[1,len]
len=s.length()-1;
t=s;
for(int i=2;i<=len;i++){
nxt[i]=nxt[i-1];
while(nxt[i] && s[i]!=s[nxt[i]+1])nxt[i]=nxt[nxt[i]];
nxt[i]+=(s[i]==s[nxt[i]+1]);
}
return ;
}
vector<int> match(string s){
//查看s中字符串t的位置
int len_s=s.length();
int j=0;
vector<int>ans;
for(int i=0;i<len_s;i++){
while(j && s[i]!=t[j+1])j=nxt[j];
if(s[i]==t[j+1])j++;
if(j==len){
ans.pb(i+1-len+1);
//记录起始位置
j=nxt[j];
}
}
return ans;
}
}T;
int tot,head[maxn],nx[maxn],to[maxn];
void add(int x,int y){to[++tot]=y;nx[tot]=head[x];head[x]=tot;}
int n,k;
string a;
int sz[maxn];
void dfs(int x,int fa){
sz[x]=1;
for(int i=head[x];i;i=nx[i]){
int v=to[i];if(v==fa)continue;
dfs(v,x);sz[x]+=sz[v];
}
return ;
}
int main(){
n=read();k=read();cin>>a;
a="!"+a;T.init(a);
for(int i=1;i<=n;i++){
add(i,T.nxt[i]);
add(T.nxt[i],i);
}
dfs(0,0);
for(int i=n;i;i=T.nxt[i]){
if(sz[i]>=k){
for(int j=1;j<=i;j++)cout<<a[j];puts("");
return 0;
}
}
puts("-1");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号