good problems-5
因为是与运算,不妨一位一位的处理,
2进制位从高往低枚举是否能把第i位加入到答案(搜索是否能由起点到终点)
能到达就答案加(1<<i)(i为当前枚举的2进制位),并将原图中的点改变
比如:
2*2的图
4 7
3 4
枚举第2位,那么图转变为
1 1
0 1
问题等效到给你一个01矩阵,找一条从起点到终点的全1路径,这个bfs处理就行
然后将原图改变为
4 7
(3) 4
(3)的含义就是接下来枚举第j位(i>j)时不考虑3这个点了
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=1e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int X[4]={0,0,1,-1};
int Y[4]={1,-1,0,0};
int n,m;
int dis[1200][1200],v[1200][1200],book[1200][1200],vis[1200][1200];
int sn,zn;
struct ver{
int x,y;
}s[maxn],z[maxn];
struct wzq{
int x,y,dis;
wzq(int a,int b){x=a,y=b;}
};
bool bfs(int pos){
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){
dis[i][j]=0;
if(book[i][j]&(1<<pos) && v[i][j])vis[i][j]=1;
else vis[i][j]=0;
}
queue<wzq>q;
for(int i=1;i<=sn;i++){
if(vis[s[i].x][s[i].y]){
q.push(wzq(s[i].x,s[i].y));
dis[s[i].x][s[i].y]=1;
}
}
while(!q.empty()){
wzq u=q.front();q.pop();
int x=u.x,y=u.y;
for(int i=0;i<4;i++){
int xx=x+X[i],yy=y+Y[i];
if(xx>n || xx<1 || yy>m || yy<1 || !vis[xx][yy] || !v[xx][yy] || dis[xx][yy])continue;
q.push(wzq(xx,yy));
dis[xx][yy]=1;
}
}
for(int i=1;i<=zn;i++){
if(dis[z[i].x][z[i].y]){
for(int j=1;j<=n;j++)for(int k=1;k<=m;k++){
v[j][k]=(v[j][k]&dis[j][k]);
}
return 1;
}
}
return 0;
}
int main(){
int t=read();
while(t--){
n=read();m=read();
sn=read();for(int i=1;i<=sn;i++)s[i].x=read(),s[i].y=read();
zn=read();for(int i=1;i<=zn;i++)z[i].x=read(),z[i].y=read();
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)v[i][j]=1,book[i][j]=read();
int ans=0;
for(int i=30;i>=0;i--){
if(bfs(i))ans+=(1<<i);
}
printf("%d\n",ans);
}
return 0;
}
/*
1
3 9
3
2 9
2 3
3 7
2
3 8
2 8
6 14 3 0 6 1 14 0 18
4 16 1 15 17 3 19 1 17
16 12 18 3 17 6 14 14 0
*/
2.G - Pre-Order
大致题意就是
给一个n个点的树的dfs遍历顺序a[],求出符合dfs遍历顺序的树的个数
其中若一个节点有多个儿子,先遍历编号小的儿子
题解:
树形区间dp
设dp[l][r]为a[]区间为[l,r]的点以一个虚点为根的树的方案数
有两种可能
1.节点l没有兄弟节点
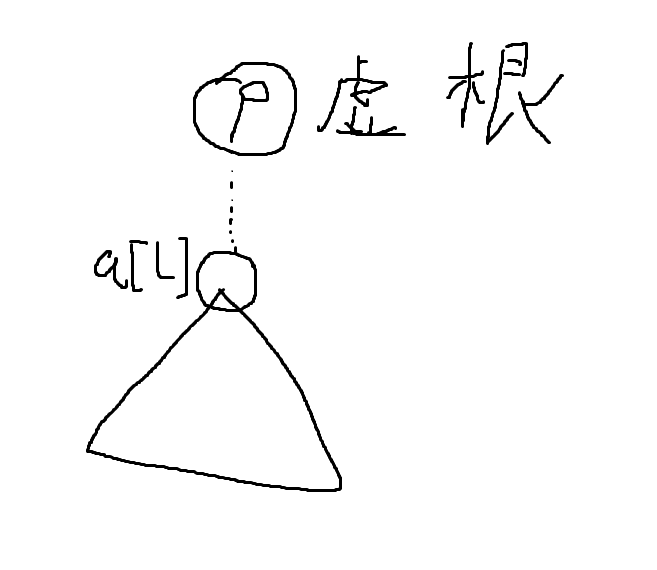
dp[l][r]=dp[l+1][r]
2.节点l有兄弟节点,且兄弟节点k满足a[l]<a[k]
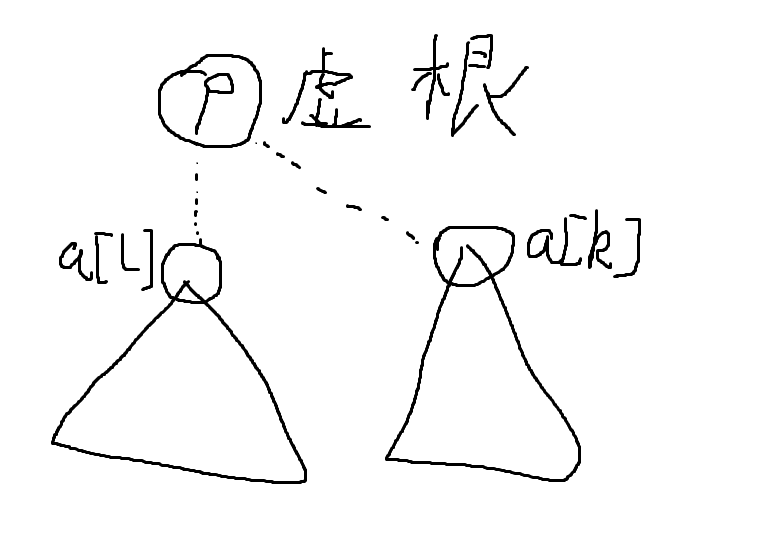
dp[l][r]+=dp[l+1][k-1]*dp[k][r](\(l+1\leq k \leq r)\)
为什么乘dp[k][r]就行,万一有很多个兄弟节点?
其实dp[k][r]就包含了有跟k为互为兄弟节点的情况
万一 l+1>k-1?
dp[l+1][k-1]就是只有l节点一个,l没有其它儿子,所以dp[l+1][k-1]=1
同时dp[i][i]=1
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#include<set>
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=500+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,p[maxn];
ll dp[maxn][maxn];
int main(){
n=read();
for(int i=1;i<=n;i++)p[i]=read(),dp[i][i]=dp[i+1][i]=1;
for(int len=2;len<=n;len++){
for(int l=1;l<=n;l++){
int r=l+len-1;
if(r>n)break;
dp[l][r]=dp[l+1][r];
for(int k=l+1;k<=r;k++){
if(p[l]<p[k])(dp[l][r]+=dp[l+1][k-1]*dp[k][r]%MOD)%=MOD;
}
}
}
printf("%lld\n",(dp[2][n]%MOD+MOD)%MOD);
return 0;
}
3.F - Operations on a Matrix
题目大意:
有n*m的矩阵,初始为0,有如下操作
1.所有行的[l,r]列加x
2.第i行全改为x
3.查询第i行j列的值
题解:
首先考虑每一行
不难看出对某一行进行操作2,则之前的所有对该行的操作都无效
考虑对于具体的某个点影响,比如下图,白色为1操作,蓝色为2操作,红色为3操作

对于最后一次询问,我们的答案应该为3+2+1=6
其实也就是红色到最近的蓝色的和,也就是前缀和相减
\(记树状数组f[t][i],query(f[t][i])为到第t个询问的列[1,i]的前缀和(操作1改变f[t][i]数组,操作2因为是对特定行操作,单独考虑)\)
\(last[t][i]为到第t个询问,第i行上一个操作2的时间t'\)
\(val[i]为当第i个询问为操作2时的x\)
\(那么当第t个询问是查询(i,j),则答案为f[t][j]-f[last[t][i]][j]+val[last[t][j]]\)
但是这样数组开不下
考虑离线
\(不难发现-f[last[t][i]][j]+val[last[t][j]]对某些操作3是一定的\)
\(那么我们就只用建树状数组f[i],query(f[i])表示当前[1,i]的前缀和\)
\(把last[t][i]相同的操作3提前加上-f[last[t][i]][j]+val[last[t][j]]就行\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=3e5+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,m,q;
ll f[maxn];
int lowbit(int x){return x&(-x);}
void add(int l,ll val){
for(int i=l;i<=m;i+=lowbit(i))f[i]+=val;
return ;
}
ll query(int r){
ll ans=0;
for(int i=r;i>0;i-=lowbit(i))ans+=f[i];
return ans;
}
struct wzq{
int pos,l;
wzq(int a,int b){pos=a;l=b;}
};
ll ans[maxn];
int main(){
n=read();m=read();q=read();
vector<vector<int> >s;s.push_back({});
vector<vector<wzq> >sub(q+1);
vector<int>last(n+1);
for(int i=1;i<=q;i++){
int opt=read();
if(opt==1){
int l=read(),r=read(),x=read();
s.push_back({opt,l,r,x});
}
else if(opt==2){
int pos=read(),x=read();
s.push_back({opt,pos,x});
last[pos]=i;
}
else {
int pos=read(),l=read();
s.push_back({opt,pos,l});
sub[last[pos]].push_back(wzq(i,l));
}
}
for(int i=1;i<=q;i++){
if(s[i][0]==1){
add(s[i][1],s[i][3]);
add(s[i][2]+1,-s[i][3]);
}
else if(s[i][0]==2){
int pos=s[i][1],x=s[i][2];
for(auto j: sub[i]){
ans[j.pos]-=query(j.l);
ans[j.pos]+=x;
}
}
else {
int pos=s[i][1],l=s[i][2];
ans[i]+=query(l);
cout<<ans[i]<<endl;
}
}
return 0;
}
4.操作题
保证题目有解,那么n一定是x的倍数,那么n一定能用x进制表示
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,char>
using namespace std;
const int maxn=3e6+4101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int main(){
int t=read();
while(t--){
ll n=read(),x=read();
if(x<=1){puts("0");continue;}
vector<pa>ans;
ll now=0;
now=n-now;ll nn=x;
int pos=0;
while(now>0){
if(now%nn){
for(int i=1;i<=(now%nn)/(nn/x);i++)ans.push_back(make_pair(1,'a'));
now-=(now%nn);
}
ans.push_back(make_pair(2,'b'));
nn*=x;pos++;
}
cout<<ans.size()<<endl;
for(auto i:ans)cout<<i.first<<" "<<i.second<<endl;
}
return 0;
}
//1000000000
5.D - Together Square
令f(x)表示x质因数分解中所有幂次为奇数的素因子的乘积,那么x*y是完全平方数当且仅当f(x)=f(y),然后O(n)数数
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=3e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int is[maxn],prime[maxn],tot;
void getprime(int n){
for(int i=2;i<=n;i++){
if(!is[i])prime[++tot]=i;
for(int j=1;j<=tot && prime[j]<=n/i;j++){
is[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
return ;
}
vector<ll>cun;
int main(){
ll n=read();
getprime(800);
ll ans=0;
for(ll i=1;i<=n;i++){
ll ii=i,ji=1;
for(int j=1;j<=tot;j++){
if(prime[j]>ii)break;
int cnt=0;
while(ii%prime[j]==0){
cnt++;
ii/=prime[j];
}
if(cnt&1)ji*=prime[j];
}
ji*=ii;
cun.push_back(ji);
}
sort(cun.begin(),cun.end());
ll last=0;
for(int i=0;i<cun.size();i++){
if(i==0){last=1;continue;}
if(cun[i]!=cun[i-1]){
ans+=last*last;
last=1;
}
else last++;
}
ans+=last*last;
cout<<ans;
return 0;
}
6.F - Rectangle GCD
考虑当h1=1,h2=n,w1=1,w2=n时的情况,其他情况类似
当前条件\((1 \leq i \leq n, 1\leq j \leq n)\)
要求所有\(a_i+b_j\)的gcd
就等于
所有\(a_i+b_1\)和所有\(b_j-b_{j-1} (2\leq j \leq n)\)的gcd
也就等于
\(a_1+b_1\)和所有\(b_j-b_(j-1) (2\leq j \leq n)\)和所有\(a_i-a_{i-1} (2\leq i \leq n)\)的gcd
这是因为gcd(a,b)=gcd(b-a,a)
所以令\(c[i]=a[i]-a[i-1],d[i]=b[i]-b[i-1]\)
用线段树维护区间的gcd
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=3e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int gcd(int a,int b){
if(a<b)swap(a,b);
if(b==0)return a;
return gcd(b,a%b);
}
struct Tree{
int t[maxn];
int tr[maxn];
void build(int k,int l,int r){
if(l==r){tr[k]=t[l];return ;}
int mid=(l+r)>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
tr[k]=gcd(tr[k<<1],tr[k<<1|1]);
return ;
}
int query(int k,int l,int r,int L,int R){
if(L>R)return -1;
if(L<=l && r<=R)return tr[k];
int mid=(l+r)>>1;
int x1=-1;
if(mid>=L)x1=query(k<<1,l,mid,L,R);
if(mid<R){
int xx=query(k<<1|1,mid+1,r,L,R);
if(x1==-1)x1=xx;
else x1=gcd(x1,xx);
}
return x1;
}
}T1,T2;
int n,q;
int a[maxn],b[maxn];
int main(){
n=read();q=read();
for(int i=1;i<=n;i++)a[i]=read(),T1.t[i]=abs(a[i]-a[i-1]);
for(int i=1;i<=n;i++)b[i]=read(),T2.t[i]=abs(b[i]-b[i-1]);
T1.build(1,1,n);T2.build(1,1,n);
while(q--){
int h1=read(),h2=read(),w1=read(),w2=read();
int ans=a[h1]+b[w1];
int x1=T1.query(1,1,n,h1+1,h2);
int x2=T2.query(1,1,n,w1+1,w2);
if(x1==-1)x1=ans;
if(x2==-1)x2=ans;
ans=gcd(ans,gcd(x1,x2));
printf("%d\n",ans);
}
return 0;
}
7.计算题



具体见https://zhuanlan.zhihu.com/p/524270760
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
typedef unsigned long long ull;
using namespace std;
const int maxn=3e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct sh{
ull base=100071;
ull p[maxn],hs[maxn],rv[maxn];
int n;char s[maxn];
void init(string str){
n=str.length();
for(int i=1;i<=n;i++)s[i]=str[i-1];
p[0]=1;
for(int i=1;i<=n;i++){
hs[i]=hs[i-1]*base+s[i];
p[i]=p[i-1]*base;
}
for(int i=n;i;i--)rv[i]=rv[i+1]*base+s[i];
return ;
}
ull que(int l,int r){
return hs[r]-hs[l-1]*p[r-l+1];
}
ull rev(int l,int r){
return rv[l]-rv[r+1]*p[r-l+1];
}
bool check(int l,int r){
return que(l,r)==rev(l,r);
}
}S;
int n;
string s;
int main(){
n=read();cin>>s;
ll ans=0;S.init(s);
for(int i=0;i<n;i++){
int L=1,R=n-i;
if(S.check(L,R)){
if((R-L+1)&1)ans+=26;
else ans++;
}
else {
int l=1,r=(L+R)>>1;
while(r>=l){
int mid=(l+r)>>1;
if(S.que(L,mid)==S.rev(R-mid+1,R))l=mid+1;
else r=mid-1;
}
r=R+1-l;
if(S.check(l+1,r-1))ans+=2;
}
}
printf("%lld",ans);
return 0;
}
8.E - Lucky Numbers
不难发现当\(A_1\)确定了,整个序列就确定了
假设\(A_1=x\),则\(A_2=S_1-x,A_3=S_2-A_2=S_2-S_1+x,A_4=S_3-S_2+S_1-x\)····
不难发现,除了x以外,其他是不变的(设不变的为b_i)
A可以表示为\(A_i=k_ix+b_i,k_i=\pm 1\)
若\(A_i是luck numberX_j\),则\(x=X_j-b_i或x=b_i-X_j\)
那么对于确定的\(k_i,b_i\)就可以确定某些x是可以使当前\(A_i是luck的\)
那么我们可以用map<ll,int>mm;来记录mm[i]:x=i时序列的lucknumber的个数
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=3e5+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,m;
ll s[maxn],xx[maxn];
map<ll,int>mm;
//mm[i]表示x=i的构造序列A的lucknumber的个数
void add(ll k,ll b){
if(k==1){
//x+b
for(int i=1;i<=m;i++)mm[xx[i]-b]++;
}
else {
//x-b
for(int i=1;i<=m;i++)mm[b-xx[i]]++;
}
return ;
}
int main(){
n=read();m=read();
for(int i=1;i<n;i++)s[i]=read();
for(int i=1;i<=m;i++)xx[i]=read();
ll k=1,b=0;add(k,b);
for(int i=1;i<n;i++){
k=-k;
b=s[i]-b;
add(k,b);
}
int ans=0;
for(auto x:mm)ans=max(ans,x.second);
printf("%d\n",ans);
return 0;
}
9.F - Pre-order and In-order
题目大意是给出先序遍历和后序遍历来求树
首先普通做法就是递归,在中序遍历的某个区间找到对应先序遍历区间最早出现的点就是当前根节点(此处根节点可能并不是整个树的根节点,而是非叶子节点)
事实上这就是笛卡尔树
我们把中序遍历每个点的权值改为它在先序遍历出现的位置,那么我们就跟就中序遍历来构造笛卡尔树就行了
建完树后,通过先序和中序遍历跟输入比较来判断是否存在
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#include<set>
#include <bits/stdc++.h>
#define ll long long
#define pa pair<ll,int>
using namespace std;
const int maxn=3e5+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
const double eps=1e-12;
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,a[maxn],b[maxn],c[maxn],d[maxn],e[maxn];
int top,st[maxn],ls[maxn],rs[maxn];
int get(int id){return b[id];}
void build(){
st[top=1]=1;
for(int i=2;i<=n;i++){
while(d[st[top]]>d[i] && top)top--;
if(!top)ls[get(i)]=get(st[top+1]);
else ls[get(i)]=rs[get(st[top])],rs[get(st[top])]=get(i);
st[++top]=i;
}
return ;
}
vector<int>aa,bb;
void dfs(int x){
if(x==0)return ;
aa.push_back(x);
dfs(ls[x]);
bb.push_back(x);
dfs(rs[x]);
return ;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
c[a[i]]=i;
}
for(int i=1;i<=n;i++){
b[i]=read();
d[i]=c[b[i]];
}
build();dfs(1);
for(int i=1;i<=n;i++){
if(a[i]!=aa[i-1] || b[i]!=bb[i-1]){puts("-1");return 0;}
}
for(int i=1;i<=n;i++)cout<<ls[i]<<" "<<rs[i]<<endl;
return 0;
}
10.F - Cumulative Cumulative Cumulative Sum
题目大意是给一个序列A,可以进行单点修改,多次询问A的三次前缀和数组D的某些位置的值
对于这种题,一般是把\(D_x\)表示出来,然后进行化简为多个部分,每个部分可用数据结构维护起来
\(D_x\)显然可以用差分的性质算出来
表示如下
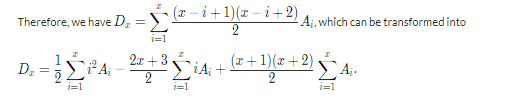
那么这3个部分分别用树状数组维护即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=1e6+10101;
const int inf=2147483647;
const int MOD=998244353;
const double eps=1e-9;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
ll power(ll x,ll y){
ll ans=1;
while(y){
if(y&1)ans=ans*x%MOD;
y>>=1;x=x*x%MOD;
}
return ans;
}
int n,q;
ll a[maxn];
struct FT{
ll f[maxn];
int lowbit(int x){return x&(-x);}
void add(int x,ll val){
val%=MOD;
for(int i=x;i<=n;i+=lowbit(i))(f[i]+=val)%=MOD;
return ;
}
ll query(int x){
ll ans=0;
for(int i=x;i>0;i-=lowbit(i))ans+=f[i];
return ans;
}
}T0,T1,T2;
void Add(int i,int k){
T0.add(i,a[i]*k);
T1.add(i,a[i]*i*k%MOD);
T2.add(i,(a[i]*i%MOD)*i*k);
return ;
}
int main() {
n=read();q=read();
for(int i=1;i<=n;i++){a[i]=read();Add(i,1);}
while(q--){
int opt=read();
if(opt==1){
ll x=read(),v=read();
Add(x,-1);a[x]=v;Add(x,1);
}
else {
ll x=read();
ll ans=(((x+1)*(x+2)%MOD)*power(2,MOD-2)%MOD)*T0.query(x)%MOD;
ans+=((-3-2*x)*power(2,MOD-2)%MOD)*T1.query(x)%MOD;ans%=MOD;
ans+=power(2,MOD-2)*T2.query(x)%MOD;ans%=MOD;
printf("%lld\n",(ans%MOD+MOD)%MOD);
}
}
return 0;
}


