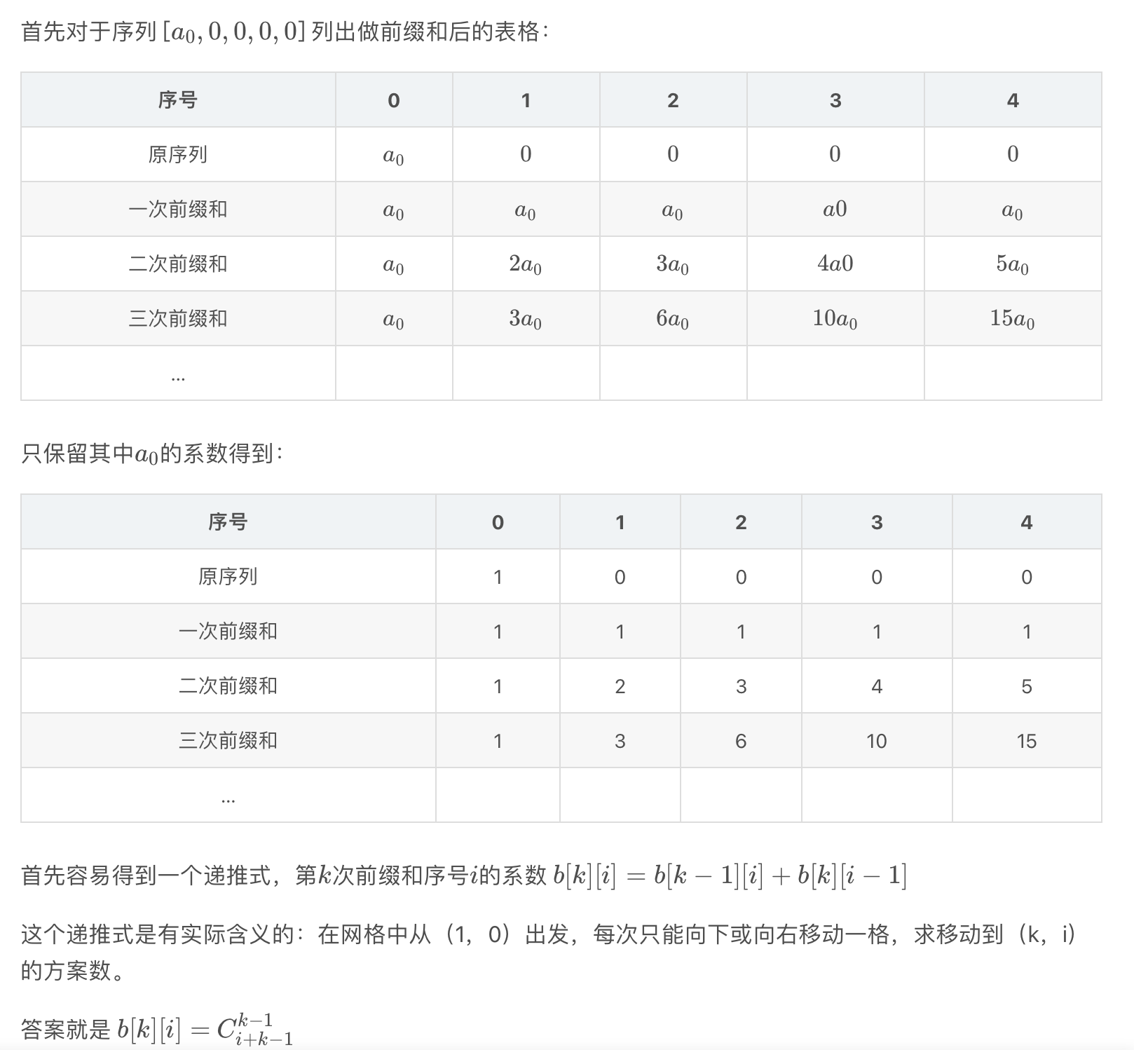
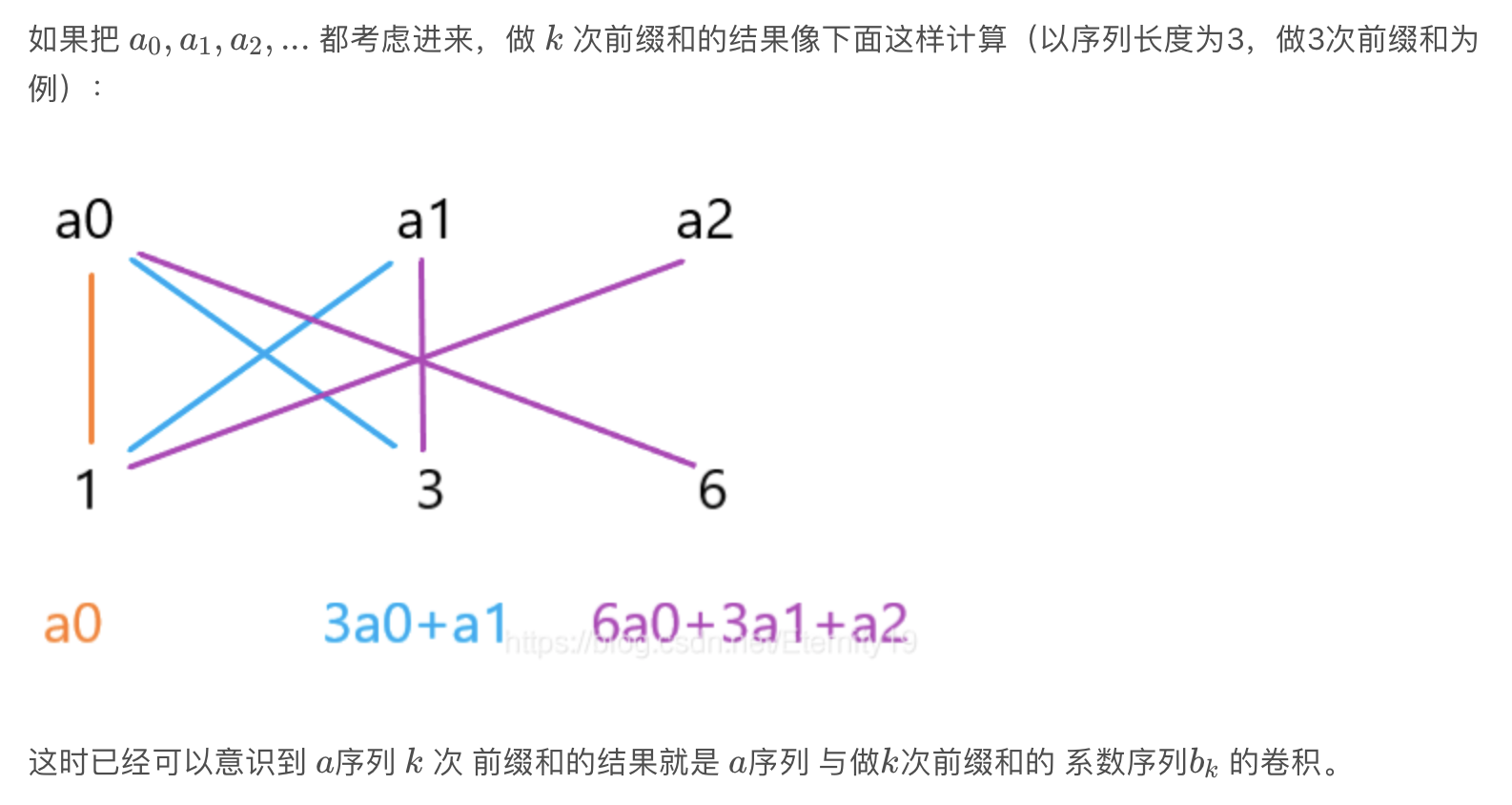
差分应用
前缀和和差分
令\(sum_i=\sum_{j=1}^i a_j\)
那么sum[]的差分数组就是a[],
a[]的前缀和数组为sum[]
普通差分
1.积木大赛
每次操作为区间操作,可看作差分b[l]++,b[r+1]--
所以题目所给的a[]就是差分数组b[]的前缀和
差分数组的正负是相互抵消的,记录正的和就是操作次数
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=2e6+101;
const int MOD=1e9+7;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,h[maxn];
int main(){
n=read();
for(int i=1;i<=n;i++)h[i]=read();
int ans=0;
for(int i=1;i<=n;i++){
if(h[i]-h[i-1]>0)ans+=h[i]-h[i-1];
}
printf("%d",ans);
return 0;
}
2.division
注:下述加平方和等差数列应用,是从l一直加到末尾
若要区间操作,在r+1后加个负的对应多项式
加一个等差数列
a[] 0 0 0 1 2 3 4 5 0 0
d[] 0 0 0 1 1 1 1 1 -5 0 //差分数组
dd[] 0 0 0 1 0 0 0 0 -6 0 //差分的差分数组
1.牛牛的Link Power I
每个“1”对后面的影响都是一个等差数列
相当于向后加了个等差数列
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=2e6+101;
const int MOD=1e9+7;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,book[maxn],a[3][maxn];
int main(){
n=read();
char ch[maxn];scanf("%s",ch);
for(int i=1;i<=n;i++){
if(ch[i-1]=='1'){
a[2][i+1]++;
a[2][n+1]--;
book[i]=1;
}
}
for(int i=1;i>=0;i--){
for(int j=1;j<=n+1;j++){
(a[i][j]+=a[i][j-1]+a[i+1][j])%=MOD;
}
}
ll ans=0;
for(int i=1;i<=n;i++){
(ans+=book[i]*a[0][i])%=MOD;
}
printf("%lld",ans);
return 0;
}
加平方
a[] 0 0 0 0 0 1 4 9 16 25 36 0 0 0
d[] 0 0 0 0 0 1 3 5 7 9 11 -36 0 0
dd[]0 0 0 0 0 1 2 2 2 2 2 -47 36 0
d'[] 0 0 0 0 0 1 1 0 0 0 0 -49 83 -36
1.小w的糖果
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=1e5+101;
const int MOD=1e9+7;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int t,n,m;
void pre_sum(ll a[]){
for(int i=1;i<=n;i++){
(a[i]+=a[i-1])%=MOD;
}
}
int main(){
t=read();
while(t--){
n=read();m=read();
ll d[4][maxn];memset(d,0,sizeof(d));
while(m--){
int type=read(),pos=read();
if(type==1)d[1][pos]++;
else if(type==2)d[2][pos]++;
else d[3][pos]++,d[3][pos+1]++;
}
pre_sum(d[3]);
pre_sum(d[3]);
pre_sum(d[2]);
for(int i=1;i<=n;i++)(d[1][i]+=d[2][i]+d[3][i])%=MOD;
pre_sum(d[1]);
for(int i=1;i<=n;i++)printf("%lld ",d[1][i]);
printf("\n");
}
return 0;
}
区间加多项式
数学定理:最高次项为n次的n阶多项式做n+1阶差分后余项为常数
加一个区间多项式,可以先将多项式进行n+1次差分,加到原数组的n+1阶差分数组上
例如多项式\(2x^3+x+1\)

多项式\(2x^2+x+2\)

不难发现n次多项式进行n+1次差分,差分数组的有n+1位有数
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=1e5+101;
const int MOD=1e9+7;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
void pre_sum(ll a[],int len,int cnt){
while(cnt--){
a[0]=0;
for(int i=1;i<=len;i++)(a[i]+=a[i-1])%=MOD;
}
}
void D(ll a[],int len,int cnt){
while(cnt--){
a[0]=0;
for(int i=len;i>0;i--)(a[i]-=a[i-1])%=MOD;
}
}
void print(ll a[],int len){
for(int i=1;i<=len;i++)printf("%lld ",a[i]);cout<<endl;
}
ll f(ll c[],int len,ll x){
ll base=1,ans=0;
for(int i=len;i;i--){
(ans+=base*c[i])%=MOD;
base=base*x%MOD;
}
return ans;
}
int n,m,q;
ll a[maxn];
int main(){
n=read();m=read();q=read();
for(int i=1;i<=n;i++)a[i]=read();
D(a,n,6);
while(m--){
int l=read(),r=read(),k=read();ll c[12];
for(int i=1;i<=k+1;i++)c[i]=read();
ll c1[12],c2[12];
for(int i=1;i<=10;i++)c1[i]=f(c,k+1,i);
for(int i=1;i<=10;i++)c2[i]=-f(c,k+1,i+r-l+1);
D(c1,10,6);D(c2,10,6);
for(int i=1;i<=10;i++){
(a[i+l-1]+=c1[i])%=MOD;
(a[i+r]+=c2[i])%=MOD;
}
}
pre_sum(a,n,7);
while(q--){
int l=read(),r=read();
printf("%lld\n",((a[r]-a[l-1])%MOD+MOD)%MOD);
}
return 0;
}
高阶前缀和
性质1:若一个数组%一个比较大的质数,该数组的做前缀和的循环节是这个模数,比如做k次前缀和等于做k%MOD次前缀和
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=3e6+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
typedef vector<ll> Poly;
ll read(){
ll x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
ll power(ll x,ll y){
ll ans=1;
while(y){
if(y&1)ans=ans*x%MOD;
y>>=1;x=x*x%MOD;
}
return ans;
}
int rev[maxn];
void get(int bit){
for(int i=0;i<(1<<bit);i++)rev[i]=(rev[i>>1]>>1)|((1&i)<<(bit-1));
return ;
}
void ntt(ll *a,int n,int f){
get(log2(n));
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1;i<n;i<<=1){
ll wn=power(3,(MOD-1)/(i<<1))%MOD;
if(f==-1)wn=power(wn,MOD-2);
for(int j=0;j<n;j+=i<<1){
ll w=1,x,y;
for(int k=0;k<i;k++,w=wn*w%MOD){
x=a[k+j];y=a[k+j+i]*w%MOD;
a[j+k]=(x+y)%MOD;a[j+k+i]=(x-y)%MOD;
}
}
}
if(f==1)return ;
int nv=power(n,MOD-2);
for(int i=0;i<n;i++)a[i]=a[i]*nv%MOD;
return ;
}
ll n,k,a[maxn],ki[maxn];
void init(){
k=(k%MOD+MOD)%MOD; //性质1
ki[0]=1;
for(ll i=1;i<n;i++){
ki[i]=(ki[i-1]*power(i,MOD-2)%MOD)*(i+k-1ll)%MOD;
}
return ;
}
int main(){
n=read();k=read();init();
for(int i=0;i<n;i++)a[i]=read();
int lens=n<<1,bit=ceil(log2(lens));lens=(1<<bit);
ntt(ki,lens,1);ntt(a,lens,1);
for(int i=0;i<lens;i++)ki[i]=ki[i]*a[i]%MOD;
ntt(ki,lens,-1);
for(int i=0;i<n;i++)printf("%lld ",(ki[i]%MOD+MOD)%MOD);
return 0;
}
高维前缀和,又叫做子集前缀和
例如二维前缀和
一般地,\(sum_{i,j}=sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+a_{i,j}\)
转化
\(sum_{i,j}=a_{i,j}\)
\(sum_{i,j}+=sum_{i,j-1}\)
\(sum_{i,j}+=sum_{i-1,j}\)
也就是先列做前缀和,再行做前缀和
换句话说就是对每一维做前缀和
1.智乃酱的子集与超集
首先考虑2个物品A,B
设T[0][0]=0,T[1][0]=A,T[0][1]=B,T[1][1]=A+B
用2维数组表示A,B选不选的价值
那么对T数组做二维前缀和,S[1][1]=A+B+A+B,表示所有[1][1]子集的价值和
那么对于这道题,可以写出个20维的前缀和ps[][][][][]......
进行状态压缩,ps[0]~ps[(1<<n)-1]
点击查看代码
#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#define ll long long
#define pa pair<int,int>
using namespace std;
const int maxn=1e7+101;
const int MOD=998244353;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
int x=0,f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
return x*f;
}
int n,m;
ll a[maxn],ps_back[maxn],ps[maxn];
//ps[][][][][][].......
int main(){
n=read();m=read();
for(int i=0;i<n;i++)a[i]=read();
int maxbit=1<<n;
for(int i=0;i<maxbit;i++){
ll sum=0;
for(int j=0;j<n;j++){
if(i&(1<<j))sum^=a[j];
}
ps[i]=ps_back[i]=sum;
}
for(int i=0;i<n;i++){
//枚举第几维做前缀和
//ps[x][x][i][x][x].....
for(int j=0;j<maxbit;j++){
//对于第i维,ps[1]+=ps[0];做前缀和
if(j&(1<<i))ps[j]+=ps[j^(1<<i)];
else ps_back[j]+=ps_back[j^(1<<i)];//做后缀和
}
}
while(m--){
int k=read(),now=0;
for(int i=1;i<=k;i++){
int p=read()-1;now|=(1<<p);
}
printf("%lld %lld\n",ps[now],ps_back[now]);
}
return 0;
}