The Sum of the k-th Powers

题目描述

题解

根据第二类斯特林数可知
\(n^m=\sum_{k=0}^m S_2(m,k)n^{\underline{k}}\)
所以
\(f(n)=\sum_{i=1}^ni^k=\sum_{i=1}^n\sum_{j=0}^k S_2(k,j)i^{\underline{k}}\)
\(\:\:\:\:\:\:\:\:\:=\sum_{j=0}^k S_2(k,j)\sum_{i=1}^ni^{\underline{k}}=\sum_{j=0}^k S_2(k,j)\cdot\frac{(n+1)^{\underline{j+1}}}{j+1}\)
具体证明

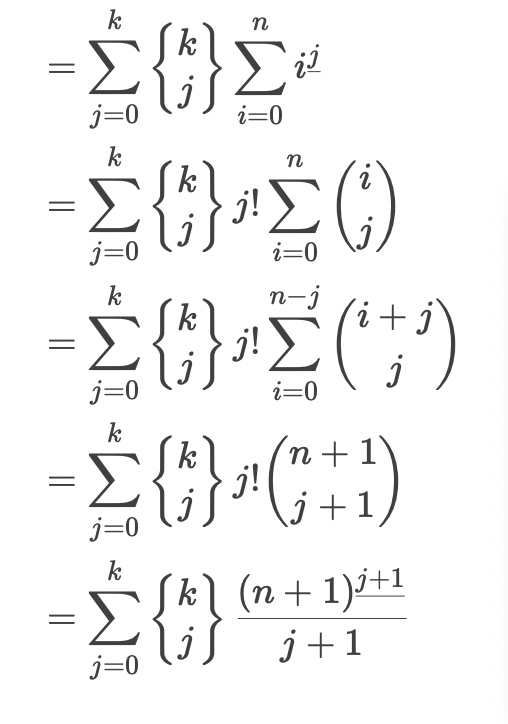
可见f(n)是一个k+1次多项式
考虑拉格朗日插值，只要求出k+2个点，就能求出f(n)
暴力求出\(f(0),f(1),···,f(k+1)\),时间复杂度为\(O(k\cdot logk)\)
则\(f(n)=\sum_{i=0}^{k+1}f_i\prod_{j\not=n}\frac{n-j}{i-j}\)
这是特殊的拉格朗日，通过预处理\(O(k)\)即可求出答案
总时间复杂度为\(O(k\cdot logk)\)

点击查看代码

#include<functional>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<map>
#define ll long long 
using namespace std;
const int maxn=1e6+101;
const int MOD=1e9+7;
const int inf=2147483647;
const double pi=acos(-1);
int read(){
    int x=0,f=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
    for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
    return x*f;
}
ll f[maxn],n,k,G=1,pre[maxn],ba[maxn];
ll power(ll x,ll y){
    ll ans=1;
    while(y){
        if(y&1)ans=ans*x%MOD;
        x=x*x%MOD;y>>=1;
    }
    return ans;
}
int main(){
    n=read();k=read();
    for(int i=1;i<=k+2;i++)f[i]=(power(i,k)+f[i-1])%MOD;
    for(int i=1;i<=k+2;i++)G=G*(n-i)%MOD;
    if(n<=k+2){printf("%lld",(f[n]%MOD+MOD)%MOD);return 0;}
    pre[0]=1;ba[0]=1;
    for(int i=1;i<=k+1;i++){
        pre[i]=(pre[i-1]*i)%MOD;
        ba[i]=(ba[i-1]*(-1)*i)%MOD;
    }
    ll ans=0;
    for(int i=1;i<=k+2;i++){
        ll now=f[i]*G%MOD;
        now=now*power(n-i,MOD-2)%MOD;
        now=now*power(pre[i-1],MOD-2)%MOD*power(ba[k+2-i],MOD-2)%MOD;
        ans=(ans+now)%MOD;
    }
    printf("%lld",(ans%MOD+MOD)%MOD);
    return 0;
}