容斥原理
定理
设S是一个有限集,\(A_1,A_2,···,A_n\)是S的n个子集,则
\(|\bigcup_{i=1}^nA_i|=\sum_{i=1}^n(-1)^{i-1}\cdot\sum_{1 \leq j_1< j_2···< j_i\leq
n}|\bigcap_{k=1}^{i}A_{j_k}|\)
\(|S-\bigcup_{i=1}^nA_i|=\sum_{i=0}^n(-1)^i\cdot\sum_{1 \leq j_1< j_2···< j_i\leq
n}|\bigcap_{k=1}^{i}A_{j_k}|\)\((\bigcap \emptyset=S)\)
若\(x\in S-\bigcup_{i=1}^{n}A_i\),在\(i=0\)时被算了1遍
若\(x\in \bigcup_{i=1}^nA_i,x\in A_{k1},A_{k2},A_{k3}···,A_{kl}\),
\(\sum_{i=0}^l (-1)^i\cdot{l \choose i}=(1-1)^l=0\),因此x会被算0遍
综上该公式等式两边成立
应用
不定方程解的数量
求不定方程\(x_1+x_2+···+x_k=n\)的解的数量,\(x_i\)为整数,且\(l_i \leq x_i \leq r_i(1\leq i\leq k)\)
令\(\:\) \(S=\{x_1+x_2+···+x_k=n的所有满足l_i\leq x_i的解\}\)
\(\quad A_i=\{ x_1+x_2+···+x_k=n的所有满足r_i < x_i的解\}\)
则
\(ans=|S-\bigcup_{i=1}^nA_i|=\sum_{i=0}^n(-1)^i\cdot\sum_{1 \leq j_1< j_2···< j_i\leq
n}|\bigcap_{k=1}^{i}A_{j_k}|\)
求解\(\sum_{1 \leq j_1< j_2···< j_i\leq n}|\bigcap_{k=1}^{i}A_{j_k}|\)
两种情况:
1.\(p\in \{j_1,j_2,···,j_i\}, x_p\geq r_i+1\)
2.\(p \notin \{j_1,j_2,···,j_i\}, x_p\geq l_i\)
则\(\sum_{1 \leq j_1< j_2···< j_i\leq n}|\bigcap_{k=1}^{i}A_{j_k}|\)共有\(2^k\)种方案
每种方案\({n+k-1-\sum_{i=1}^{k}(l_1 \: or \: r_i+1) \choose k-1}\)
所以\(ans=|S-\bigcup_{i=1}^nA_i|=\sum_{i=0}^n(-1)^i\cdot\sum_{1 \leq j_1< j_2···< j_i\leq n}{n+k-1-\sum_{i=1}^{k}(l_1 \: or \: r_i+1) \choose k-1}\)
容斥原理符号
设S是一个有限集,\(a_1,a_2,···,a_n\)是n种性质
记\(N(a_i)\)为S中有\(a_i\)性质的元素的数量,特殊的,记\(N(1)=|S|\)
记\(N(1-a_i)\)为S中没有\(a_i\)性质的元素的数量
记\(N(a_{i1},a_{i2},···a_{ik})\)为S中同时有\(a_{i1},a_{i2}···a_{ik}\)的元素的数量
记\(N(a\pm b)=N(a)\pm N(b)\)
容斥原理可以写为
\(N((1-a_1)(1-a_2)···(1-a_n))=\sum_{i=0}^{n}(-1)^i \cdot \sum_{1\leq j_1<j_2···<j_i\leq n}N(a_{j_1}a_{j_2}···a_{j_i})\)
对于有些性质有,有些性质没有,公式可以写为
\(N(a_1···a_x(1-a_{x+1})···(1-a_{n+x}))=\sum_{i=0}^{n}(-1)^i \cdot \sum_{x+1\leq j_1<j_2···<j_i\leq n+x}N(a_1···a_xa_{j_1}a_{j_2}···a_{j_i})\)
例题
1.https://ac.nowcoder.com/acm/contest/219/B
2.CQOI2012局部最小值 题解
3.Mike and Foam 题解
二项式反演
公式一
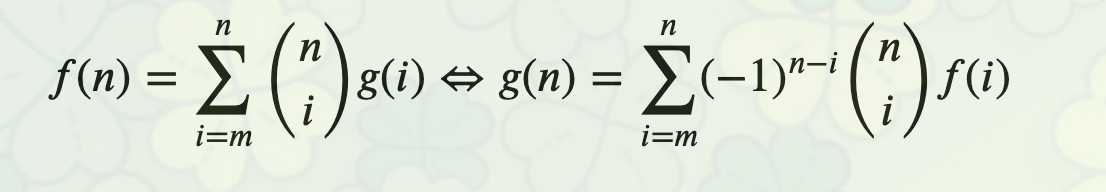
公式二
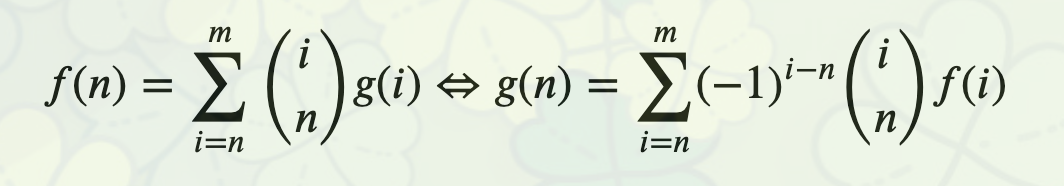



 浙公网安备 33010602011771号
浙公网安备 33010602011771号