对accuracy、precision、recall、F1-score、ROC-AUC、PRC-AUC的一些理解
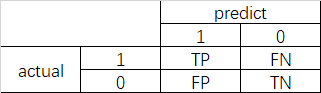
最近做了一些分类模型,所以打算对分类模型常用的评价指标做一些记录,说一下自己的理解。使用何种评价指标,完全取决于应用场景及数据分析人员关注点,不同评价指标之间并没有优劣之分,只是各指标侧重反映的信息不同。为了便于后续的说明,先建立一个二分类的混淆矩阵 ,以下各参数的说明都是针对二元分类
1.准确率 accuracy
准确率:样本中类别预测正确的比例,即
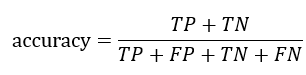
准确率反映模型类别预测的正确能力,包含了两种情况,正例被预测为正例,反例被预测为反例,当我们对类别为1、类别为0的关注程度一致时(类别为对称的),准确率是一个不错的评价指标,但是如果我们更关注样本被预测为类1的情况,准确率就不是一个合适的指标,因为通过它你无法知道正例的预测情况,因为反例的预测情况也包含在其中,而这并不是我们关注的。
2.精确率 precision
精确率:被预测为正例的样本中,真实的正例所占的比例,即
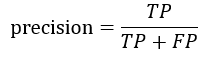
精确率反映模型在正例上的预测能力,该指标的关注点在正例上,如果我们对正例的预测准确性很关注,那么精确率是一个不错的指标。例如在医学病情诊断上,患者在意的是“不要误诊”,此时精确率是合适的指标。
精确率是受样本比例分布影响的,反例数量越多,那么其被预测为正例的数量也会越多,此时精确率就会下降,因此当样本分布不平衡时,要谨慎使用精确率。
3.召回率 recall
召回率:真实的正例样本中,被预测为正例的样本所占的比例,即
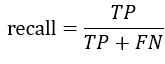
召回率反映模型在正例正确预测上的覆盖率,有点“不允许有一条漏网之鱼”的感觉,如果我们关注的是对真实正例样本预测为正的全面性,那么召回率是很好的指标。例如在一些灾害检测的场景中,任何一次灾害的漏检都是难以接受的,此时召回率是很合适的指标(宁可错杀一百,不可放过一人,哈哈哈)。
召回率是不受样本比例不平衡影响的,因为它只关注的是正例样本上的预测情况。
4.F1-score
F1-score :兼顾精准率与召回率的模型评价指标,其定义为:
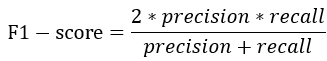
当对精准率或者召回率没有特殊要求时,评价一个模型的优劣就需要同时考虑精准率与召回率,此时可以考虑使用F1-score。F1-score实际上是precision与recall的调和平均值,而调和平均值的计算方式为
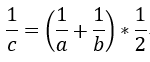
调和平均值有特点呢?|a - b| 越大,c 越小;当 a - b = 0 时,a = b = c,c 达到最大值,具体到精准率和召回率,只有当二者大小均衡时,F1-score 才高。同时,F1-score也考虑了Precision、Recall数值大小的影响,只有当二者都比较高时,F1-score才会比较大。
5.ROC-AUC
ROC(receiver operating characteristic curve)是一条曲线,其横轴表示的是FPR(False Positive Rate)——错误地预测为正例的概率,纵轴表示的是TPR(True Positive Rate)——正确地预测为正例地概率,二者地计算如下:
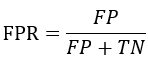
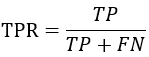
从TPR地计算方式来看,其实际上就是召回率。前面已说过,Recall不受样本不平衡的影响,实际上FPR也具有该特点。ROC曲线类似于下图,TPR、FPR地取值范围均在0~1之间
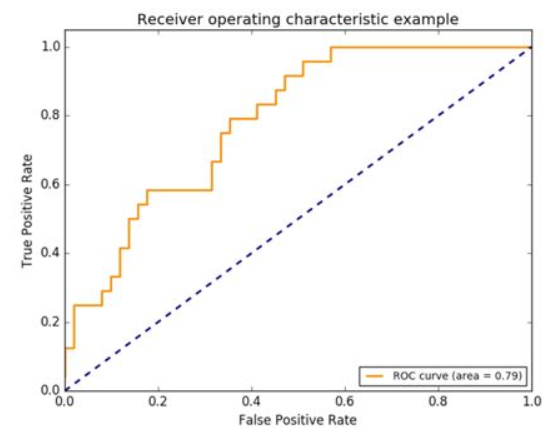
那么这张图是如何绘制出来地呢?在分类模型中(以决策树分类模型为例),可以计算出样本属于正例/反例的概率,这个概率是基于叶子节点上的样本计算的,如果一个叶子节点上包含了m个正例、n个反例,那么当测试集上的样本被划分到该叶子节点上时,其被预测为正例的概率即为:m/(m+n)。获知样本被预测为正例的概率之后,设定一个概率阈值,大于等于该阈值的样本属于正例,小于该阈值的样本属于反例,这样就可以计算出TPR和FPR,在0~1上递增该阈值(需选定一个递增步长),就可以计算出一些列的TPR与FPR,即可绘制出ROC;在回归模型中,是一样的方式。
AUC(area under curve)是一个数值,从定义上可以直观的看到其表征的意思——曲线与坐标轴围成的面积,ROC-AUC即表示的是ROC曲线与坐标轴围成的面积。
很明显的,TPR越大、FPR越小,模型效果越好,因此ROC曲线越靠近左上角表明模型效果越好,此时AUC值越大,极端情况下为1。与F1-score不同的是,AUC值并不需要先设定一个阈值。ROC-AUC不仅可以用来评价模型优劣,通过分析ROC曲线得形状特点还可以帮助分析模型,这在之后将专门写一篇博客来说明。
6.PRC-AUC
PRC与ROC类似,包括曲线的绘制方式,不同的是PRC的横轴是Recall,纵轴是Precision。一个PRC曲线的例子为
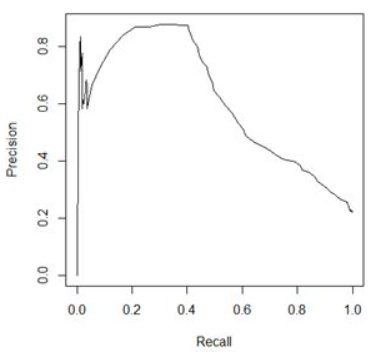
Recall越大、Precision越大表明模型效果越好,此时PRC曲线靠近右上角,AUC值也越大。与ROC-PRC不同的是,Precision受样本不平衡的影响,相应的PRC也会因此形状变化。因此,在样本数据量比较大时,ROC会比较稳定,一般选择ROC-AUC来评价模型是较为合适的。而当阈值确定时,Precision、Recall、F1-score都可以用来评价模型




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?