关联分析（一）：频繁项集及规则产生

关联分析用于发现隐藏在大型数据集中有意义的联系，属于模式挖掘分析方法，其为人熟知的经典应用当属沃尔玛超市里“啤酒与尿布”的关系挖掘了。关联分析的应用领域非常多，当数据集类型比较复杂时，进行关联分析采用的手段也相对复杂，本篇从最简单的事务数据集着手，对关联分析进行解读。对大型事务数据集进行关联分析时，有两个问题要考虑：

发现关联模式时耗费的计算量
发现的关联模式是否可信

关联分析方法主要就是围绕这两个问题展开。

1.基本概念

二元属性事务集

在购物篮事务数据集中，每一条记录中属性只有购买(1)和不购买(0)两种情况，不统计商品的任何其他信息，如下所示

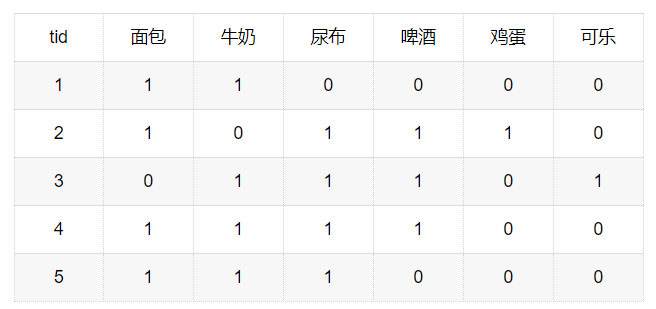
对上面的商品购买记录来说，购买商品更加引人关注，人们一般不关注未购买的商品，这样的二元变量即称为非对称二元变量。非对称二元变量

关联规则

关联规则是形如 $X\rightarrow Y$ 的表达式， $X$ 和 $Y$ 是两个不相交的项集，这里的项集指的是购买商品的集合。 $X$ 称为规则前件， $Y$ 称为规则后件。

支持度

支持度表示的是项集 $X,Y$ 同时出现在购买记录中的频繁程度，以上面事务集为例，假设 $X$ 表示啤酒， $Y$ 表示尿布，则啤酒 $\rightarrow$ 尿布的支持度为

$s(X\rightarrow Y)=\frac{N(X,Y)}{N}=\frac{3}{5}=0.6$

频繁项集

项集的支持度超过设定的阈值时，该项集即称为频繁项集。

置信度

置信度指的是 $Y$ 出现在包含 $X$ 的力矩中的频繁程序，以上面事务集为例，假设 $X$ 表示啤酒， $Y$ 表示尿布，则啤酒 $\rightarrow$ 尿布的置信度为

$c(X\rightarrow Y)=\frac{N(Y|X)}{N(X)}=\frac{N(X,Y)}{N(X)}=\frac{3}{3}=1$

依据这几条基本概念，我们可以考虑一下从上述的事务集中提取规则，例如已经提到的 “啤酒 $\rightarrow$ 尿布”，还可以提取“啤酒、面包 $\rightarrow$ 尿布”等等，对于一个包含 $d$ 项的事务集，可提取的规则总数为

$R=3^{d}-2^{d+1}+1$

可以看到规则的总数是指数级的，这给关联分析带来了难度。现在再考虑一下开篇提到的那两个问题，如何减少规则提取时的计算量、如何保证提取的规则可信？这并不容易做到，但是引入规则支持度和置信度能改善这个问题。若一条规则中包含的项出现次数少，那么它可能是偶然出现，不足以被认为是数据集中隐藏的规则，支持度就是用于剔除这一类候选规则；置信度用于衡量规则的可靠性，若规则后件项集 $Y$ 出现在规则前件项集 $X$ 中的比例越高，我们就越有理由相信这条规则是可信的。那么基于支持度和置信度来提取规则是不是一定可行的呢？答案是不一定，支持度和置信度用于提取规则时都需要设置阈值，这本身就是比较难做的事情，阈值高低会导致规则数量发生显著变化，而且置信度中并没有考虑规则侯后件的支持度，这在一些情况下会产生不合理的规则，关于这一点我们在系列后面的文章中再详细讨论。

用支持度和置信度去筛选规则，在提取完所有规则后再筛选也是不可行的，这会耗费大量的计算时间，因此一般的做法是：先提取频繁项集，再从频繁项集中提取规则。

2.频繁项集的产生

在生成频繁项集时，可以从两个方向考虑来节省计算时间：<1>减少候选频繁项集<2>通过采用高级的数据结构，减少项集搜索时间。

2.1 Apriori算法中的频繁项集产生方法

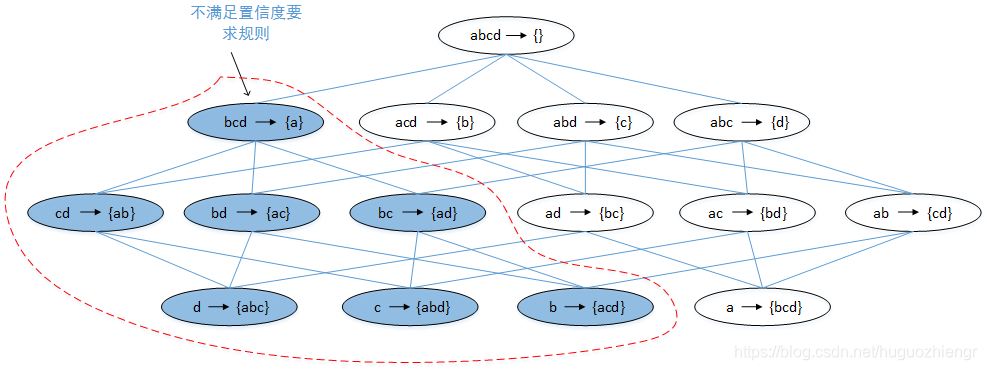
在Apriori算法中，用到了两条先验原理：<1>如果一个项集不是频繁项集，那么该项集的超集也必定不是频繁项集；<2>如果一个项集是频繁项集，那么该项集的子集也是频繁项集，利用这两条先验原理可以大大较少候选频繁项集的数量。

第一步：设定支持度阈值，扫描一遍数据集，找出1-项(项集中只包含1个商品)频繁项集。

第二步：从1-项频繁项集中生成候选2-项频繁项集，然后再次扫描数据集，找出2-项频繁项集。以此类推，依据 $(k-1)$ -项频繁项集生成候选 $k$ -项频繁项集，然后扫描数据集，找出 $k$ -项频繁项集， $k=3,4,...$ ，直到无法再生成频繁项集。

2.1.1 候选项集

在以上过程中，涉及到多次数据集的扫描，每次从候选频繁项集中找出频繁项集时都需要扫描一次数据集，而且还有另外一个问题，如何从 $(k-1)$ -项频繁项集中生成候选 $k$ 项频繁项集？对该问题，可以采用 $F_{k-1}\times F_{k-1}$ 方法：

$F_{k-1}\times F_{k-1}$ 方法是通过合并一对 $k-1$ 项频繁项集生成候选 $k$ 项频繁项集，不过要求这一对 $(k-1)$ -项频繁项集的前 $k-2$ 个项相同，但是有1-项频繁项集生成2-项候选频繁项集时不需如此。举个例子，现在有两个3-项频繁项集 {面包，牛奶，啤酒}、{面包，牛奶，可乐}，那么这两个3-项频繁项集就可以生成一个4-项候选频繁项集 {面包，牛奶，啤酒，可乐}，但是{面包，牛奶，啤酒}和{面包，尿布，可乐}就无法按照此规则生成4-项候选频繁项集。按照这种方式生成候选频繁项集，有一个要求，数据集中的项必须先制定好排序，所有记录中的项需要按照该排序规则排列。为什么会采用这种方式生成候选频繁项集呢？还是以 {面包，牛奶，啤酒，可乐}为例，如果其为频繁项集，那么其子集也是频繁项集，因此{{面包，牛奶，啤酒}、 {面包，牛奶，可乐}均为频繁项集，基于这种原理能减少候选频繁项集的数量。

2.1.2 候选项集支持度计数

从候选频繁项集中筛选出频繁项集时需要对它们进行支持度计数。支持度计数的方法这里介绍两种，一种是线性扫描数据集，将数据集中的每一条记录与所有候选频繁项集进行匹配并计数，最终得到频繁项集。在候选频繁项集比较多的情况下，这种方法中进行比较的次数会较多，此时可以采用第二种方法；第二种方法中，使用Hash结构计数，能较少比较次数。实施过程如下：

例设数据集中包含的项的集合为 { 面包，牛奶，尿布，啤酒，鸡蛋，可乐}，并且顺序按此顺序排列，那么可以依次给它们分配标号为{1，2，3，4，5，6}。假设通过上文中介绍的内容我们得到的候选的3-项频繁项集为{1，2，3}、{1，3，5}、{1，3，6}、{2，4，6}、{2，5，6}、{3，4，6}，{3，5，6}、{4，5，6}，由于是3-项候选集，因此利用Hash函数 $h(p)=p \: \:mod \: \:3$ 来建立3-项候选频繁项集的Hash树，得到

依次扫描数据集中的每一条记录，提取每条记录中所有可能的3-项集。假设现在有一条记录为{1，3，5，6}，那么其可提取的3-项集为{1,3,5}，{1,3,6}，{1,5,6,}，{3,5,6} ，那么将每一个3-项放在第一步建立的Hash树中寻找对应的桶，然后与桶中的3-项候选频繁项集比较，并为相同的候选项集增加计数。

经过以上的两步，就完成了所有3-项候选项集的支持度计数。需要强调的是，对于 $k$ -项候选频繁项集的计数，使用Hash函数 $h(p)=p \: \:mod \: \:k$ 来建立于 $k$ -项候选频繁项集的Hash树，然后扫描数据集，提取每一条记录中所有的 $k$ -项集，放入hash树中，对 $k$ -项候选频繁项集进行支持度计数。

2.2 FP增长算法

Apriori算法中每次从 $k$ -项候选频繁项集中找出频繁项集时，都需要扫描一次数据集，这在数据集及项集较大时是比较大的负担，FP增长算法通过采用特殊的数据集存储结构——FP树，找出全部的频繁项集只需要扫描数据集两次，能有效的减少计算过程。

之前看到过一篇对FP Tree及FP 增长算法的介绍，讲解得比较清晰，推荐一下。我这里就不再介绍FP 增长算法了，大家可以直接参考链接中的文章学习。

https://www.cnblogs.com/zhengxingpeng/p/6679280.html

3.规则的生成方法

规则是从频繁项集中提取的，也可以说是从最大频繁项集中提取。最大频繁项集指的是包含项最多的频繁项集，从最大频繁项集(可能有多个)中一定可以提取出所有的频繁项集。由于在生成频繁项集阶段，就已经获取了所有的频繁项集的支持度计数，因此通过置信度提取规则时，不再需要扫描数据集。

在生成频繁项集时，可以依据两条先验规则减少计算量，而在提取关联规则时，只有一条规则可以利用：如果规则 $X\rightarrow Y$ 不满足置信度要求，那么 $X-X^{`}\rightarrow Y+X^{`}$ 也不满足置信度要求，其中 $X^{`}$ 是 $X$ 的子集。这条规则可以这样理解，假设置信度阈值为 $\alpha$ ，则有

$\frac{S(X,Y)}{S(X)}<\alpha$

由于 $X^{`}$ 是 $X$ 的子集，因此 $X^{`}$ 的支持度一定不小于 $X$ ，假设 $X^{`}=X+k$ ，则有

$\frac{S(X-X^{`},Y+X^{`})}{S(X-X^{`})}=\frac{S(X,Y)}{S(X)+k}<\frac{S(X,Y)}{S(X)}<\alpha$

基于该规则，可以采用如下的方式从最大频繁项集中提取规则：

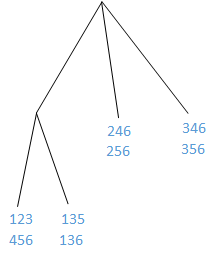
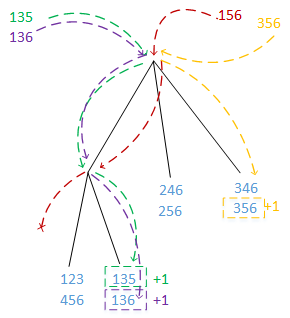
<1>找出后件只有一个项的所有满足置信度要求的规则。对于那些后件只有一项(假设为 $a$ )、不满足置信度要求的规则，可以直接剔除掉所有后件中包含 $a$ 的规则，例如

<2>通过合并两个规则后件生成新的候选规则，然后判断其是否满足置信度要求，同样的，剔除掉那些不满足置信度要求的候选规则，以及这些规则中后件的超集对应的规则。例如，通过合并 $abd\rightarrow c$ 与 $abc\rightarrow d$ 得到新的候选规则 $ab\rightarrow cd$ ，如果该规则不满足置信度要求，那么后件中包含 $cd$ 的候选规则也均不满足要求，例如 $a\rightarrow bcd$ 。