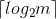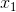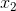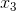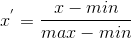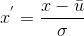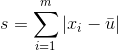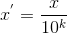数据预处理过程
数据预处理过程会占用很多时间,虽然麻烦但也是必不可少且非常重要的一步。在数据能用于计算的前提下,我们希望数据预处理过程能够提升分析结果的准确性、缩短计算过程,这是数据预处理的目的。本文只说明这些预处理方法的用途及实施的过程,并不涉及编程方面内容,预处理的过程可以用各种各样的语言编程实现来实现。我个人始终是秉持着这样的观点:没有任何一种方法可以一成不变的被应用于任何任务中,依据实际任务选择、调整处理方法是最佳的。
数据预处理方法可以大致分为四类:数据清理、数据集成、数据变换和数据规约。
1.数据清理
数据清理主要针对数据数值上的各种异常情况的处理,根据数值异常情况的不同,数据清理常见的有以下:缺失值处理、离群和噪声值处理、异常范围及类型值处理。
1.1 缺失值处理
缺失值使数据记录丢失了部分信息,一些鲁棒性不佳的模型也会因为缺失值而导致无法计算数据。缺失值的处理,一般有以下两种思路:丢弃和估计。
- 丢弃
你可以只丢弃缺失项处的值,也可以丢弃包含缺失项的整条数据记录,这得看该条数据记录上其它的数据是否有价值,尤其是在数据样本较少的情况下,需要权衡一番。
- 估计
不想丢弃缺失值时,对缺失值进行估计是必要的。估计的方法有多种,最直接的是让有经验的人员手工填写,除此之外其它的常见方法有如下几种:
(1) 替代。用缺失值所处属性上全部值的平均值(此时也可以加权重)、某个分位值代替。对于时间序列,则可以用相邻数据记录处值(或平均值)替代。
(2) 填充。 可以用与缺失值记录“相似”记录上的值来填充缺失值,不过这里需要先定义“相似”,这可能会是一个棘手的问题,用K最邻近、聚类等方法估计缺失值都是这种思想。对于时间序列,则可以用插值的方法,包括线性和非线性插值。
(3) 基于统计模型的估计。基于非缺失的值构建统计模型,并对模型参数进行估计,然后再预测缺失处的值。
1.2 离群和噪声值处理
实际上噪声含括的范围比较广泛,对计算过程无用或造成干扰的都可以称为噪声,像1.1节中所说的缺失值、1.3节中说的异常范围及类型值均属于噪声的范畴,之所以在这里和离群点放在一起讨论,是想说一下噪声和离群点间的关系。
离群点则是指与数据总体特征差别较大的。离群点是否是噪声需要在实际的应用场景中判断,比如像建立系统总体的模型,那么离群点就可以视为噪声,它对模型的创建毫无用处,甚至会影响模型的准确性。而在一些模式识别领域中,那么就要考虑离群点是噪声,还是对模式创建有用的点,因为模式总是针对少量样本的。
上面关于离群点的说明中,我觉得应该有一个“离群点数据量”的问题,个别与数据总体特征差别较大的点我们可以称为离群点,但如果有相当一部分量与数据总体特征差别较大的点,那此时就要考虑这些点能不能被称为离群点了。
相比于处理离群点,识别离群点是一个更重要的问题。识别离群点的方法有很多,比如基于统计学的方法、基于距离的检测、基于密度的监测(如DBSCAN聚类法)等,本文中不涉及这方面的内容,故不作详解介绍。
噪声的处理可以针对具体情况进行,离群点处理前先要判断该点是否是有用的,若是无用点则可以当做噪声处理,若是有用的则保留。
1.3 异常范围及类型值处理
异常范围类型是指记录数据超过了当前场景下属性可取值的范围,比如记录一个人的身高为300cm,或者月收入为负值,这显然也是不合理的。异常类型值是指属性取值类型记录错误,比如记录一个人的身高为“超重”。
对于以上两种情况,如果数据记录异常是有规律的,比如身高记录下的数据依次为“312,365,373...”那么可能原纪录是“112,165,173...”。如果异常值是随机的,那么可以将这些异常值当做缺失值处理。
2.数据集成
数据集成主要是增大样本数据量。
2.1 数据拼接
数据拼接在数据库操作中较为常见,它将多个数据集合为一个数据集。数据拼接依赖的是不同数据集间有相同的属性(或关键字或其它的特征)(不同类型数据库下拼接的原则可能不同,如关系型数据库、半关系型数据库和非关系型数据库下)。
3.数据变换
数据变换包含的方法众多,作用也不尽相同。数据变换的目的可以简单的概括为改变数据的特征,方便计算及发现新的信息(这个概括可能不太合适。。。)。常见的数据变换过程包含以下方法:离散化、区间化、二元化、规范化(有的地方也成称为标准化)、特征转换与创建、函数变换。
3.1 离散化
当我们不太关心值的小范围变化,或者想要将连续属性当成离散属性处理时,可以使用离散化方法,这可以简化计算,提高模型准确率。
一般来说,离散化是将排序数据划分为多个空间,例如将 [0,10] 离散为[0,2),[2,4),[4,6),[6,8),[8,10],这样可以将一个连续取值的属性转换为离散取值的属性来处理。
我们还可以将一个取值比较“密”的离散属性进一步离散化,这是离散化中的另外一种情况,例如一个离散属性的取值集合为{0,1,2,3,4,5,6,7,8,9,10},那么此时可以将该取值集合进一步离散化为{0,1,2},{3,4,5},{6,7,8},{9,10}。
在实际应用时,对于标量型取值,可以将每个离散区间用一个新的值表示,不管是采用取中位值还是求平均等方法;而对于标称型取值,可以重新定义一组标称取值表示,例如 {极差,差,较差},{一般},{较好,好,极好},可以重新定义成{下},{中},{下},也可以选取其中一个值来代替整体,如 {差},{一般},{好}
离散化过程需要考虑两点:(1)如何确定离散区间(集合)的个数 (2)如何将取值映射到离散化后的区间(集合)中。为了方便以下不再单独强调集合,统一称为区间。
针对第一个问题,可以采用非监督和监督的离散化方法来确定离散区间的个数,一旦离散集合划分完毕,那么对于第二个问题,直接将数据映射到其分类值上即可。监督和非监督的区别在于区间划分过程是否利用样本类别信息,一般来说利用类别信息能达到更好的区间划分结果,但计算量也会大一些。
非监督的离散方法主要包括等宽离散化、等频率离散化、聚类离散化等,离散过程不利用样本的分类信息。
- 等宽离散化。使每个离散区间据有相同的宽度。类似于将 [0,10] 离散为[0,2),[2,4),[4,6),[6,8),[8,10]的过程
- 等频离散化。等频离散化过程确保每个区间内包含相同的样本数。
- 聚类离散化。利用算法自身优化目标进行,聚类完成后每个簇就对应着一个区间,常用的如K均值聚类。
监督的离散化方法主要包括,基于熵(或信息增益)的区间离散化、卡方分裂算法离散化等。这里只介绍基于一种简单的基于熵的离散过程。
- 基于熵的离散化。设
是样本集中包含的样本个数,
是样本集中类别的总数,
是划分的第
个区间中的样本个数,
是第
个区间中属于类别
的个数,则第
个区间的熵可以定义为:
其中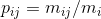
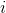
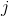

其中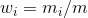
(1) 把区间上每个值看做分割点,将样本集划分为两部分,寻找使得总体熵最小的一种划分方式。
(2) 选择已划分的两个区间中熵最大的一个,继续步骤(1)
(3)当划分区间达到指定数目,或者满足指定终止条件(如区间划分后总体的熵变化小于指定阈值)时停止区间划分
对于多维属性,可以将其每一维上的值进行离散化,然后组合起来得到离散的多维空间。实际上离散化方法分类远不止监督和非监督这两种,感兴趣的同学可以参考这篇文章(https://blog.csdn.net/CalCuLuSearch/article/details/52751218)进行更详细的了解,后面如果有需要的话再单独写文章介绍离散化过程。
3.2 二元化
有一些算法中要求属性为二元属性(例如关联模式算法),即属性的取值只能为0或1(当然其它二元取值形式都可以,如Yes和No,只是都可以转化为0和1表示),此时就要用到属性二元化的过程。
二元化的过程是用多个二元属性来表示一个多元属性。假设属性取值有
以上的二元化过程可能会导致属性间关系复杂化,例如上表中属性
当一个属性取值数量较多时,这种做法会引入过多的属性值,此时可以在二元化之前先进行离散化,减少属性取值。
3.3 规范化
数据规范化是调整属性取值的一些特征,比如取值范围、均值或方差统计量等,这在一些算法中很重要。常见的规范化方位有:最小-最大规范化、z-score规范化、小数定标规范化。
- 最小-最大规范化
该方法是对原始数据的线性变换,将数值映射到[0,1]上,如身高(cm)和体重(kg)的取值范围相差较大,在邻近度分析中就需要进行最小-最大规范化,消除量纲(单位)的影响。该过程为
其中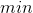
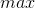
- z-score规范化
该方法也成为标准差规范化,处理后属性取值的均值为0,方差为1。该过程为
其中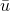
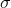
- 小数定标规范化
该方法通过移动小数点的位置,将数值映射到[-1,1]上。该过程为
其中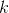
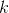
3.4 特征转换与创建
对有一些时间序列,可以通过傅里叶变换、小波变换、EMD分解等方法得到数据的频域或其它类型特征,这能帮助我们从另一个角度分析问题,例如EMD分解在经济学上就有较多的应用。采用这一类方法时,一个比较重要的问题是如何解释在频域或时域上得到的新特征。
假如属性集中包含“质量”和"体积”这两种属性,那么可以利用“密度=质量/体积“的方法得到密度属性,这样就创建了一个新的属性。当然,需不需要这么做完全取决于目的。
3.5 函数变换
函数变换是一个比较宽泛的说法,上面的规范化过程也是一种函数变换过程。我们可以依据需求,选择函数来处理数据,例如当属性取值比较大时,可以用log函数来处理数据。
4.数据规约
数据规约的目的是减少数据量,降低数据的维度,删除冗余信息,提升分析准确性,减少计算量。数据规约包含的方法有:数据聚集、抽样、维规约。
4.1 数据聚集
数据聚集是将多个数据对象合并成一个数据对象,目的是为了减少数据及计算量,同时也可以得到更加稳定的特征。聚集时需要考虑的问题是如何合并所有数据记录上每个属性上的值,可以采用对所有记录每个属性上的值求和、求平均(也可以加权重)的方式,也可以依据应用场景采用其它方式。比如一家全球零售商,如果统计一天之中全球范围内所有店的全部销售数据,那么数据量会比较大且不是很有必要,此时可以将一个店内一天的销售数据进行聚集,得到一条或有限条销售数据,然后再汇总。
进行数据聚集时可能会丢失数据细节,也许这些细节正是你所关注的,这点尤为需要注意。
4.2 数据抽样
在数据预处理中提抽样,实际上就是重抽样了,目的就是为了获取数据样本中的一部分用于计算,减少计算负担。重抽样的方式与一般抽样一致。
4.3 维规约
维规约方法是为了减少属性的个数,上面提到的由质量和体积得到密度是一种维规约方式。当属性为标称类型时,没有“密度、质量、体积”这种数值上的联系,但是也可能存在其它的联系来进行维规约,例如将“机械学科、自动化学科、材料学科”同一归为“工程学”。
更一般的,是采用一些数据降维的方法。数据降维的方法有很多,本文不打算在此处详细说明降维的方法,后面会单独写一篇文章来说明数据降维的方法。有兴趣的同学可以先看看这篇文章https://www.cnblogs.com/guoyaohua/p/8855636.html
小结
数据预处理是为了得到 tidy data ,但预处理过程绝不仅仅只是以上的内容,很多处理过程与数据分析目的紧密结合的,本文只是简要的介绍一些常见的数据预处理过程。


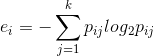
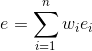
![\left [0,m-1 \right ]](https://img-blog.csdnimg.cn/20181226175715727)