经典假设检验理论记录一二

大数据环境下的假设检验问题比较复杂，目前还未详细深入了解，但其思想还是源于经典假设检验理论，故在此先对经典假设检验理论记录一二。

1.假设检验方法的作用

实际问题中很多时候需要通过样本去作推断，由于样本带有随机性，基于我们对总体的认知，有时并不确定该推断是否可信（或者说可靠），或者说偏差的程度如何，此时就可以用到假设检验方法，在我们认知范围内去判断该推断是否可信（或可靠）、偏差程度。之前看到过一段话，说假设检验方法背后的哲学思想是：“肯定一件事情有时候是很难的，但是否定一件事情就容易得多”（挺有意思的一句话，就像人们常说的“一世清明毁于一旦”啥的），该思想在概率论中，即为“小概率事件理论”。假设检验的实施过程就是利用小概率事件理论去判断推断是否可信。

2.假设检验问题的一般处理步骤

(1) 明确要处理的问题，问题的回答只能是“是”或者“否”

(2) 设计适当的观察或试验以取得样本X，X的概率分布必须与所提的问题有一定联系

(3) 把问题的一种回答（例如“是”）作为一个命题，将该命题转化到样本X的分布上，这样即得到关于后者的一个等价命题，称为假设

(4) 依据样本X的具体值，按照一定的规则，作为接受或否定假设的决定（即检验过程）

3.检验方法

当提出合适的假设后，接下来的工作主要是如何去检验提出的假设。检验的方法有很多种，每种方法一般都是针对某一方面问题而针对性提出的，下面介绍几种比较重要的检验方法。

3.1 拟合优度检验

拟合优度检验方法是K.Pearson提出的。K.Pearson认为统计的任务是对未来进行预测，故需要得到样本数据的统计模型，也即是一条分布曲线，所以他提出了矩估计法来确定这样一条分布曲线，但是得到的分布曲线对样本的拟合程度该如何判断呢？为此K.Pearson引进了一个统计量—— $\chi ^{2}$ 统计量k， $k=k(X_{1},...X_{n};F)$ ，统计量k反映样本 $X_{1},...X_{n}$ 与所拟合的分布曲线 $F$ 间的偏离，k越小，拟合程度越好，反之亦然。从一组样本中，可以计算出统计量k的值 $k_{0}$ ，也许 $k_{0}$ 会很小，总体上觉得拟合程度不错，但是还是存在这样一个问题：统计量k的值取到 $k_{0}$ 这样的程度，可以认为拟合程度比较好、可以认为样本 $X_{1},...X_{n}$ 是来自于分布曲线 $F$ 中吗？为了解决这个问题，K.Pearson证明了一个极限定理，通过该定理可以计算出概率 $P(k\geqslant k_{0})$ ,该定理为

定理：若样本 $X_{1},...X_{n}$ 是来自于分布曲线 $F$ ，则当样本大小 $n\rightarrow \infty$ 时，统计量k的分布收敛于 $\chi ^{2}_{r-1}$ ，即自由度为r-1的 $\chi ^{2}$ 分布。

至此为止，文中还未引入统计量k的定义，这个后面再引入。 $P(k\geqslant k_{0})$ 越大（小），则表明产生像 $k_{0}$ 这么大（小）的值的概率越大（小），因此 $k_{0}$ 的出现并不稀奇（比较稀奇），基于此，可以做出如下假设：

$H:$ 样本 $X_{1},...X_{n}$ 是从具有分布 $F$ 的总体中抽样得到

检验时，指定阈值 $\alpha$ ，若 $P(k\geqslant k_{0})\geq \alpha$ ，则否定 $H$ ；若 $P(k\geqslant k_{0})< \alpha$ ，则接受 $H$ 。现在开始引入统计量k，文中只讨论总体分布曲线 $F$ 完全已知的情况，对分布确定、带有参数的情况不予讨论，感兴趣的同学可以自行进一步研究。当样本X为一维时，X只取有限个不同值 $a_{1},a_{2},,,a_{r}$ ，理论分布 $F$ 集中在 $a_{i}$ 的概率为 $p_{i}$ ，则对于以上的假设可以这样提

$H:$ $P(X=a_{i})=p_{i}$

记 $v_{i}$ 为 $X_{1},...X_{n}$ 中等于 $a_{i}$ 的个数，称为观察频数， $np_{i}$ 称为理论频数，可知

${\sum_{i=1}^{r}}v_{i}=n$

则统计量k定义如下

$k=k(X_{1},,,X_{n};F)=\sum_{I=1}^{r}\frac{(v_{i}-np_{i})^{2}}{np_{i}}$

当样本X的取值为一维连续值时，则可以将X的取值空间划分为m个连续、互不相交的空间，也即是将其取值范围离散化，之后便可用上述统计量k的定义形式；当样本X为多维数据（离散取值或连续取值）时，也可以按照上述思路引入统计量k，具体过程此处不详述。

3.2 显著性检验

显著性检验是Fisher提出的，从字面上理解，该检验最终需要通过结果的显著性程度(概率)去决定是否接受假设。现在通过一个例子来了解显著性检验的思想。

为比较A、B两种施肥方法那种更优，选择15块大小近似的地，把每块地分成大小、形状一样的两小块，随机的将一块用A施肥方法，另外一块用B施肥方法，各小块的产量如下

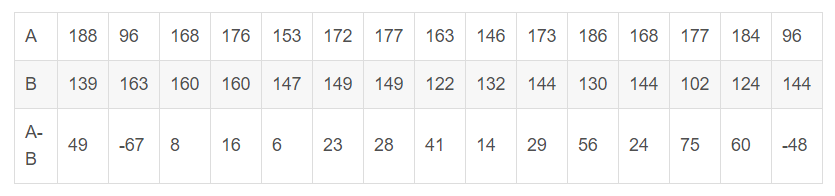
现做出假设

H: 施肥方法A与B的效果一样

由上表的产量结果，可以计算出 $\sum (A-B)=314$ ，由于每块地中的两小块是随机分给A和B的，基于提出的假设，上表中得到的产量差也可能是由于两小块地间的差别导致，因此 $(A-B)$ 的结果可能会反过来，故 $\sum (A-B)$ 的计算结果应该有 $2^{15}$ 种可能，即

$\pm (49)\pm (-67)\pm (8)...\pm (60)\pm (48)$

计算得到的314只是 $2^{15}$ 种结果中的一种，当施肥方法A与B间效果差别较大时，绝对值 $\left | \sum (A-B) \right |$ 应该取较大值，为此将 $2^{15}$ 种结果按绝对值大小从大到小排列，在假设H成立的前提下，每个值出现的概率都是 $2^{-15}$ ，而在本例中所有 $\left | \sum (A-B) \right |\geq 314$ 结果出现的概率 $p< 0.0001$ ，这个概率非常小，即便在 $\alpha =0.0001$ 的显著性水平下，我们也有理由否定假设H，由于本次观察的结果 $\sum (A-B)> 0$ ，因此认为施肥方法A的效果优于B。

通过该例，可以将显著性检验的一般过程概括如下

(1) 明确一个命题（假设）H

(2) 设计一个试验观察与假设相关的变量X，当假设H成立时，X要有明确、已知的分布

(3) 根据假设H和X的具体内容，对X可能出现的值排序，使越靠前的值对提出的假设H越不利

(4) 记x为实际观察到的X值，计算x及x更靠前的值出现的概率和 $p_{x}$ ， $p_{x}$ 越小，则对假设H越不利。

(5) 依据选择的显著性水平 $\alpha$ 来决定是否接受假设H

3.3 似然比检验

似然比检验是J.Neyman和E.S.Pearson提出一种检验方法，这是一种基于直观想法的检验方法。在说明似然比检验方法前，先介绍一下二人在假设检验问题上提出的一系列理论，合称为Neyman-Pearson理论（简称NP理论）。

(1) 问题的提法，原假设与对立假设

设有样本X，取值于样本空间 $\vartheta$ ，只知道X的分布属于一个分布族 $\left \{ F_{\theta }|\theta\in\Theta \right \}$ 。设 $\Theta _{H}$ 是 $\Theta$ 的一个非空子集，则命题 $H$ : $\theta \in \Theta _{H}$ 称为一个假设或原假设，也成为零假设，命题 $H$ 的确切含义为：存在一个 $\theta \in \Theta _{H}$ ,使X的分布为 $F_{\theta _{0}}$ 。记 $\Theta _{K}=\Theta -\Theta _{H}$ ，则命题 $K$ : $\theta \in \Theta _{K}$ 称为H的对立假设，表述

$H:\theta \in \Theta _{H}\leftrightarrow K:\theta \in \Theta _{K}$

称为一个假设检验问题。注意此处，在提出原假设 $H$ 后，也明确的给出了其对立假设 $K$ ，而拟合优度检验、显著性检验理论出现较早，当时并未考虑对立假设的问题。正如在第二小节中提到的，问题的提出十分重要，在NP理论中，这一点更显得重要，不同的问题提出方式将得到完全不同的命题 $H$ 和 $K$ 。例如3.2节中例子，假设两小块地的土地条件足够均匀，但是由于某些随机因素的影响（如人工操作差别）可能导致两小块地间产量会有所区别，以c记由A与B的不同导致的产量差，第i小块地上观察到的 $A_{i}-B_{i}=c_{i}+e_{i}$ ， $e_{i}$ 为上述随机因素导致的误差。假定 $e_{i}$ 服从均值为0的正态分布，则样本 $X_{1},...,X_{n}$ 独立，各有分布 $N(c,\sigma ^{2})$ 。原假设为 $H$ : $c=0,\sigma > 0$ 任意，对立假设为 $K$ ： $c\neq 0,\sigma > 0$ 任意。由此可知，原假设和对立假设的提出很重要，要充分考虑和利用已知的背景知识。

(2) 两类错误与功效函数

在假设检验时，错误有两类：一是 $H$ 为真但被否定了，称为第一类错误（弃真），二是 $H$ 不为真但被接收了，称为第二类错误（采伪），假设检验过程犯错是不可避免的，但我们要尽量使犯错的概率减小，为此定义了功效函数，简单的说功效函数 $\beta _{\varphi }(\theta )$ 就是当样本分布参数等于 $\theta$ 时，假设 $H$ 被否定的概率。

(3) 检验水平，限定第一类错误概率原则

若检验函数 $\varphi$ 犯第一类错误的概率总不超过 $\alpha$ （不论 $\theta$ 在 $\Theta$ 内取何值，总不超过 $\alpha$ ），则称 $\alpha$ 是检验 $\varphi$ 的水平，而 $\varphi$ 称为水平 $\alpha$ 的检验。通过这个定义，明确了通常所说的检验水平的具体含义。

现在开始介绍似然比检验。设样本X有概率函数 $f(x,\theta )(\theta \in \Theta )$ ， $\Theta _{H}$ 是 $\Theta$ 的一个非空子集，考虑本小节中提出的假设问题，可构造统计量

$LR(x)=\frac{\underset{\theta \in \Theta }{sup}f(x,\theta )}{\underset{\theta \in \Theta_{H} }{sup}f(x,\theta )}$ (1)

称为关于该检验问题的似然比。对于统计量 $LR(x)$ 可以这样理解：基于NP理论中假设的提出方式，由于 $\theta$ 肯定是属于其取值空间 $\Theta$ 的，也可以认为 $\theta$ 最大似然估计是接近其真实值的，那么当 $LR(x)$ 值越大时，表明在得到样本 $X$ 时， $\theta \in \Theta _{H}$ 的可能性越小，此时更倾向于否定假设。有了统计量 $LR(x)$ 后，定义如下检验函数 $\varphi (x)$

$\varphi (x)=\left\{\begin{matrix}1,\, \, LR(x)>C & \\ \gamma ,\, LR(x)=C & \\ 0,\, LR(x)<C & \end{matrix}\right.$ (2)

当 $\varphi (x)=1$ ，否定假设，当 $\varphi (x)=0$ 时接收假设。至此为止，似然比检验的基本思路已经明了，但是还未说明如何去确定这样一个 $C$ 值。 $C$ 值的确定根据具体应用中样本X的概率函数 $f(x,\theta )$ 确定，下面举个例子来说明似然比检验的过程

设 $X_{1},...,X_{n}\sim N(\theta ,1),H:\theta =\theta _{0}\leftrightarrow K:\theta \neq \theta _{0}$ ， $\theta _{0}$ 给定，有

$f(x_{1},...,x_{n},\theta )=(2\pi )^{-n/2}exp[\, -\frac{1}{2}\sum_{i=1}^{n}(x_{i}-\theta )^{2}\, ]$

依据极大似然估计方法，可以得到

$\underset{\theta\in \Theta _{H}}{sup}f(x_{1},...,x_{n},\theta )=f(x_{1},...,x_{n},\theta_{0} )$

$=(2\pi )^{-n/2}exp[\, -\frac{1}{2}\sum_{i=1}^{n}(x_{i}-\theta_{0} )^{2}\, ]$

$\underset{\theta\in \Theta}{sup}f(x_{1},...,x_{n},\theta )=(2\pi )^{-n/2}exp[\,-\frac{1}{2}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2} \, ]$

这里

$\bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}$

对于正态分布函数，其均值的极大似然估计即为 $\bar{x}$ ，则统计量 $LR(x)$ 计算为

$LR(x_{1},...x_{n})=exp[\, \, \frac{1}{2}(\bar{x}-\theta _{0})^{2}\, \, ]$

可以看出 $LR(x_{1},...,x_{n})$ 时 $|\bar{x}-\theta _{0}|$ 的严格增加函数，因此对于我们的假设 $H$ 有否定域 $|\bar{x}-\theta _{0}|>C$ ，注意此处 $C$ 值与公式(1)中 $C$ 值虽然代号相同，但指的不是同一个值，当然这个也不重要。依据 $\bar{x}$ 的定义，有

$\bar{x}\sim N(\theta ,\frac{1}{n})$

$\frac{\bar{x}-\theta _{0}}{\sqrt{n}}\sim N(0,1)$ (3)

此时 $\bar{x}$ 的分布为连续分布，公式(1)中检验函数 $\varphi (x)$ 取 $\gamma$ 那一行没有必要。 $C$ 值需要依据检验水平来确定，若取水平 $\alpha$ ，则依据式(3)

$C=\mu _{\alpha }/\sqrt{n}$

4.小结

以上内容简单的介绍了假设检验方法的作用及一般步骤，并介绍了几种常见的检验方法，其中还顺便提到了NP理论。可以看到，假设检验过程比较重要的是采用何种检验方法，除了以上介绍的几种检验方法，其它重要的检验方法还有正态分布均值检验中用到的 $t$ 检验、正态分布方差检验中用到的 $F$ 检验（二者都是基于似然比检验方法展开的），它们分别构造了 $T$ 统计量和 $F$ 统计量，依据这两个统计量的概率分布和检验水平来检验假设是否可接受。

posted @ 2019-05-18 15:38 hgz_dm 阅读(421) 评论(0) 编辑收藏举报

刷新页面返回顶部

hgz_dm