决策树——树的生长

分类算法非常适合预测或描述标签为二元或标称类型的数据集，对于标签为序数类型的数据集，分类技术则不太有效，因为分类技术不考虑隐藏在序数中的“序”关系，对于标签其他形式的联系如子类与超类（包含的关系），分类技术也不太适合。

本文是分类模型系列的初篇，先介绍最基本的分类/回归模型——决策树模型。决策树分类模型打算分为三篇来说明，第一篇先说明决策树生长，第二篇介绍决策树的剪枝过程，第三篇介绍常用的决策树模型算法。

1.树的生长过程

决策树的生长一般采用贪心的策略，所有训练样本都会参与到树的生长过程，树生长完成后所有训练样本都能被明确的分类。训练集 $D= \left \{ (x_{1},y_{1}),(x_{2},y_{2}),,,(x_{k},y_{k}) \right \}$ 中 $x_{i}$ 表示各样本的属性值， $y_{i}$ 表示 $x_{i}$ 的标签， $A=\left \{ a_{1},a_{2},,,a_{n} \right \}$ 表示样本的属性集，则决策树的构建方法如下

生成结点node
若D中所有样本均属于同一类别C，则将结点node标记为叶结点，其类归为类C，返回
若A为空、或者D中样本在A中属性上取值相同，则将结点node记为叶节点，其类归为D中样本数最多的类，返回
若2、3中情况均未出现时，从A中选择一个最优划分属性 $a_{*}$ ，对 $a_{*}$ 的每一个划分值，为node结点生成一个分支，令 $D_{v}$ 表示 $D$ 在 $a_{*}$ 取值为 $a_{*}^{v}$ 时的样本子集
若 $D_{v}$ 为空，则将该分支结点标记为叶结点，其类归为父结点中样本数最多的类；若 $D_{v}$ 不为空，则得到新的数据集 $D_{v}$ 和新的属性集 $A_{v}=A\setminus a_{*}$ （从 $A$ 中去掉 $a_{*}$ ），重复1~5步骤

在树的生长步骤4中，提到了“选择一个最优的划分属性 $a_{*}$ ”、“ $a_{*}$ 的每一个划分值”问题，那么该如何选择最优划分属性、划分值呢？

2.树生长过程中需要考虑的问题

正如第1节中提到的问题，在每一个内部结点上，如何选择最优划分属性、划分值呢？这正是需要考虑的问题。

2.1最优属性的度量参数

优劣的比较应该是有一个量化的评判标准的，在最优属性的抉择上，一般采用“信息增益”、“增益率”、“基尼指数”这三个参数中的一个来评判。最优属性指的是利用该属性划分结点上数据后，信息增益/增益率/基尼指数变化最大。下面以离散取值属性为例，分别介绍这几个参数

信息增益

“信息熵”在信息论中表示随机变量不确定性程度，用于样本集合中，则可以用来度量集合的纯度，也即是表征集合中样本类别数量、每中类别对应样本数量的信息。

信息熵 $Ent(D)$ 定义如下

$Ent(D)=-\sum_{i=1}^{k}p_{i}log_{2}p_{i}$ (1)

式(1)中 $p_{i}$ 为样本集 $D$ 中第 $i$ 类样本数占总样本数的比例，信息熵值越小，表示样本数据集纯度越高，当所有样本属于同一类时，纯度最高，为0。特别的，规定当 $p_{i}=0$ 时， $p_{i}log_{2}p_{i}=0$

对于离散取值属性a，其取值范围为 $\left \{ a_{1},a_{2},,,a_{k} \right \}$ ，若将内部节点node按属性a进行子女结点划分，则其样本数据集D被划分为 $D_{1},D_{2},,,D_{k}$ ，则对结点node进行划分后，其信息增益 $Gain(D,a)$ 定义为

$Gain(D,a)=Ent(D)-\sum_{i=1}^{k} \frac{N(D_{i})}{N(D)}Ent(D_{i})$ (2)

式(2)中 $N(D_{i})$ 表示样本集 $D_{i}$ 中样本数， $N(D)$ 表示样本集 $D$ 中样本数。一般而言，信息增益 $Gain(D,a)$ 越大，表示按照属性a划分后样本数据的纯度提升越大。对于取连续值的属性a，一般也是将其取值离散化。

增益率

当属性的取值数目较多时，信息增益计算结果会偏大一些，因为更多的叶子结点必然能达到更低的误分类率，信息增益也就越小。为了减小这种情况带来的不利影响，提出了增益率 $Gain\; ratio(D,a)$ ，其定义为

$Gain\, ratio(D,a)=\frac{Gain(D,a)}{IV(D,a)}$ (3)

式(3)中 $IV(D,a)$ 定义为

$IV(D,a)=-\sum_{i=1}^{k}\frac{N(D_{i})}{N(D)}log_{2}\frac{N(D_{i})}{N(D)}$ (4)

当属性的取值数目较少时，在式(3)的增益率计算结果又会偏大一些。基于此，综合考虑之后Quinlan教授提出了这样一个依据增益率选择划分属性的方法：先从待划分属性中找出信息增益高出平均水平的属性，然后再从这些信息增益结果中选择增益率最高的属性作为最终的划分属性。

基尼指数

基尼指数实际上是经济学中的概念，用来衡量财富分配的不均衡性，也可以依据该指数来选择划分属性。首先对基尼值 $Gini(D)$ 做如下定义

$Gini(D)=\sum_{i=1}^{k}\sum_{j=1,j\neq i }^{k}p_{i}p_{j}=1-\sum_{i=1}^{k}p^{2}_{i}$ (5)

式(5)中 $p_{i}$ 定义与式(1)中一致。对于 $p_{i}$ ，可以这样解释，从样本数据集D中随机抽取一个样本，该样本属于类 $i$ 的概率。因此，基尼系数可以直观的解释为：随机从数据集D中抽取两个样本，这两个样本所属类不一致的概率，该概率越小，表明数据集D的纯度越高。基于基尼值，基尼指数 $Gini\: index(D,a)$ 的定义如下

$Gini\: index(D,a)=\sum_{i=1}^{k}\frac{N(D_{i})}{N(D)}Gini(D)$ (6)

依据基尼指数选择划分属性时，选择基尼指数最小的属性。

2.2 连续型属性的划分值

在2.1节中，都是以离散取值型属性为例来定义信息增益、增益率、基尼指数，对于连续取值型属性，需先对其离散化，实际上对于连续型属性，采样后得到的样本的属性值已经是离散的，不过在选择划分值时，还要考虑训练样本中未出现的值。

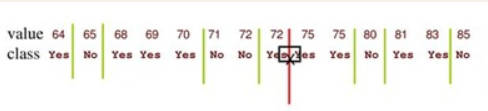
对给定的样本集D和连续型划分属性a，将D中属性a的取值从小到大排列，得到 $\left \{ a_{1},a_{2},,,a_{k} \right \}$ ，对该集合中任意两个相邻取值 $a_{i}$ 、 $a_{i+1}$ ，划分值取它们之间任意一个值时，对D来说都不影响划分结果，因此一般取二者平均值即可

$a'_{i}=\frac{a_{i}+a_{i+1}}{2} \: \: \: \: i=1,2,,,k-1$

这样就得到属性a新的划分值集合 $\left \{ a'_{1}, a'_{2},,,a'_{k-1}\right \}$ ，接着可以按照第2.1节中的方法来判断属性a是否为最佳划分属性。在计算划分值时，有一个小窍门可以注意一下，当将样本集D中属性a的取值从小到大顺序排列之后，若有一段相邻的样本类别相同，则集合 $\left \{ a'_{1}, a'_{2},,,a'_{k-1}\right \}$ 中由这一段相邻样本计算出的值可以不予以考虑，有时候这样可以减少许多计算量。

事实上不仅在连续型属性的划分值上需要处理，一些算法中要求决策树是二叉树，此时包括多个取值的离散型属性在内，划分值都需要单独处理。这个部分放在特定的算法中说明（决策树系列的第三篇）

3 树生长的终止条件

第1节中描述决策树的生长过程是一个“完全”的生长过程，生长的终止条件为：所有的样本属于同一类，或者所有的样本具有相同的属性值。从目前应用较广的决策树模型来看，这种“完全”式的生长过程是合理的，它能较小训练误差，但要得到一棵泛化误差较小的树，还需要进行剪枝处理，这将在下一篇《分类：决策树——剪枝》中说明。

posted @ 2019-01-19 19:06 hgz_dm 阅读(713) 评论(0) 编辑收藏举报

刷新页面返回顶部

hgz_dm