局部加权回归

局部加权回归(Locally Weighted Regression, LWR)

局部加权回归使一种非参数方法(Non-parametric)。在每次预测新样本时会重新训练临近的数据得到新参数值。意思是每次预测数据需要依赖训练训练集，所以每次估计的参数值是不确定的。

局部加权回归优点：

1. 需要预测的数据仅与到训练数据的距离有关，距离越近，关系越大，反之越小；
2. 可以有效避免欠拟合，减小了较远数据的干扰，仅与较近的数据有关。

对于一般训练集：

    

    

参数系统为：

    

局部加权回归原理：

图1 局部加权回归原理

线性回归损失函数J(θ)：

    

局部加权回归的损失函数J(θ)：

    

    

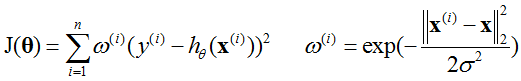
为相似度，这个相似度实际上就是SVM的高斯核函数，也就是高斯相似度。

令损失函数最小，最后得到θ。

普通线性回归参数一般为m+1，而对于局部加权的线性回归参数个数可能有无穷多个(也就是说参数个数跟样本数量相关)。

普通的线性回归，训练完成之后只保留参数，而局部线性回归中需要保留样本与参数来得到模型

参数数量有限的叫做有参模型，而参数数量无限的叫做无参模型(参数无穷多)。

 

原创文章，转载请注明出处！