机器学习基础(HGL的机器学习笔记1)
统计学习:统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科,统计学习也成为统计机器人学习[1]。
统计学习分类:有监督学习与无监督学习[2]。
统计学习三要素:模型、策略与算法[1]。
统计学习的对象:统计学习的对象是数据。统计学习从数据出发,提取数据的特征,抽取数据的模型,发现数据中的指示,又回到对数据的分析与预测中去[1]。
统计学习的目的:建立输入与输出的关系,评价输入与输出的关系,即Y = f(X) + ε。其中输入变量X可以称为预测变量、自变量、属性变量及变量。输出变量Y可以称为响应变量或因变量。ε为随机误差项,与X独立且均值为0[2]。
统计学习的目的实际上就是估计f,估计f的原因主要又两个:预测与推断[2]。
预测实际上是计算出Ẏ = ḟ(X),其中Ẏ为Y值的预测值,ḟ为f的预测。Ẏ作为Y的预测,其精确性依赖两个量,一个是可约误差,另一个是不可约误差。
证明:假设ḟ与X是固定的,则 E(Y - Ẏ)^2 = E[f(X) + ε - ḟ(X)]^2 = [f(X) - ḟ(X)]^2 + Var(ε)。其中,[f(X) - ḟ(X)]^2可约误差,Var(ε)不可约误差。
E(Y - Ẏ)^2代表预测量与实际值Y的均方根误差或期望平方根误差值。Var(ε)表示误差项ε的方差。统计学习关注的重点就是最小化可约误差。
给出损失函数,损失函数是对一次预测好与坏的一种评价,损失函数越小,模型越好。常见的有:
0-1损失函数:Y == ḟ(X) 为1,否则为0
平方损失函数:L(Y, ḟ(X)) = [Y - ḟ(X)]^2 (常用)
绝对损失函数:L(Y, ḟ(X)) = |Y - ḟ(X)|
对数损失函数:L(Y, P(Y|X)) = -log P(Y|X)
推断实际上就是理解输入X与输出Y的关系。换句话说,X的变化怎样影响Y的变化。
统计学习关心三类事情,一类是预测,一类是推断,还有一类是预测与推断的混合。
估计f的方法[2]
1. 参数法
- 首先,假设f具有一定的形式,例如,常用的假设为是f线性的,即f(X) = a0 + a1 × X1 + a2 × X2 + … + an × Xn。这是线性模型,在这个模型中只需估计a0…an这n + 1个参数。
- 一旦模型选定,可以用训练集去拟合或训练模型。常用的线性拟合方法为最小二乘法。
参数法把估计f的问题简化为估计一组参数,因为估计参数更为容易。
参数法的缺陷:选定的模型并非与真正f的在形式上一致。假设选择的模型与真实的f相差很大,那么尝试去选择更光滑的模型。但光滑度更强的模型需要更多的参数估计,且更光滑的模型可能导致过拟合。
过拟合是指学习时选择的模型所包含的参数过多,以至于出现这一模型对已知数据预测得很好,但对于未知数据预测得很差的现象[1]。
2.非参数法
非参数法不需要对函数f的形式事先做明确的假设。相反,这类方法追求的是接近数据点的估计,估计函数在去粗和光滑处理后尽可能与更多的数据点接近。
非参数法的优点:不限定函数f的具体形式,于是可能在更大的范围选择更适合f形状估计。
非参数法的缺点:无法将估计f的问题简化到仅仅对少数参数进行估计的问题,所以为了对f更为精确的估计,往往需要大量的观测点(远远超出参数法需要的观测点)。
具体方法以后介绍。
模型评估[1]
训练误差: 训练集平均误差,即
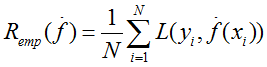
其中,N为训练集容量,L常选择平方损失函数。
测试误差:测试集平均误差,即
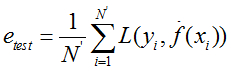
其中,N'为测试集容量,L常选择平方损失函数。
测试误差越小的方法具有更好的预测能力,更有效的方法。
模型选择——正则化与交叉验证[1]
正则化:正则化是结构风险最小化策略的实现,是载经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值越大。正则化一般形式为

其中,第一项为损失函数(经验风险),第二项为正则化,λ为调整两者间的关系系数。正则化原则根据具体问题具体分析,各种问题的形式不仅相同。
交叉验证:如果给定足够的数据,可以将简单的将数据分为三部分,分别为训练集、验证集与测试集。训练集用于训练模型,验证集用于模型选择,而测试集用于对最终学习方法的评估。主要包含有:
- 简单交叉验证:首先随机将数据分为两部分,一部分作为训练集,一部分作为测试集(一般按照70%训练集,30%测试集分配)。
- S交叉验证:将数据切分称互不相交且大小相同的子集,然后利用S-1个子集训练,用剩下一个子集测试,将这个过程对可能的S种选择重复进行,最终选出测试误差最小的模型。
- 留一交叉验证:S交叉验证的特殊形式是S = N,称为留一交叉验证,往往在数据缺乏的情况下使用,N是给定的数据集容量。
预测精度与模型解释性的权衡[2]
统计学习方法是在预测精度与模型解释性之间权衡,如果仅仅是对预测感兴趣,至于预测模型是否易于解释并不关心,所以选择光滑度更高的方法才是最优选择,但是光滑度越高解释性越低,甚至产生过拟合。
有监督学习与无监督学习[3]
有监督学习:对具有概念标记(分类)的训练样本进行学习,以尽可能对训练样本集外的数据进行标记(分类)预测。这里,所有的标记(分类)是已知的。典型的有监督学习方法:回归方法,分类方法等等。
无监督学习:对没有概念标记(分类)的训练样本进行学习,以发现训练样本集中的结构性知识。这里,所有的标记(分类)是未知的。因此,训练样本的岐义性高。典型无监督学习:聚类方法。
泛化能力[1]
泛化能力:学习方法的泛化能力是指由该方法学习到的模型对未知数据的预测能力。
泛化误差:对未知数据预测的误差,即
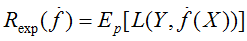
注:并没有包含[1]、[2]的全部内容,仅包含作者认为重要的内容。
[1] 《统计学习方法》,李航
[2] 《统计学习导论》,Gareth James等.
[3] http://blog.sina.com.cn/s/blog_56c221b00100gjl6.html
原创文章,转载请注明出处。




