code craft 20
题意： 一共n个人，要选p人作为队员安排在每个位置（每个人在不同位置所产生的贡献不同），另选k人作为观众。问怎么安排使得最后的总贡献最大。每个人作为观众本身的贡献为ai，作为队员在不同位置的贡献为pi
题解： 观察到p的范围很小，所以考虑状压DP。首先我们按照每个人作为观众的贡献从大到小进行排序。可以得出观众只能在前k+p人中选取。这个很容易想啦；
然后就行
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
typedef long long ll;
const int inf=0x3f3f3f3f;
struct Node{
int a,p[7];
bool operator <(const Node &b)const{
return a>b.a;
}
}s[maxn];
ll dp[maxn][200];
int main(){
int n,p,k;
cin>>n>>p>>k;
for(int i=1;i<=n;i++){
cin>>s[i].a;
}
for(int i=1;i<=n;i++){
for(int j=0;j<p;j++){
cin>>s[i].p[j];
}
}
sort(s+1,s+1+n);
memset(dp,-inf,sizeof dp);
dp[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<(1<<p);j++){///dp【i】【j】：前i个人时，队员p个位置上j状态的时候最大值
if(i-__builtin_popcount(j)<=k&&i<=k+p)///首先就是你的i就是第i个人，然后减去你的这i个人里你选的队员个数，这个值说明就是你所选的观众个数，为什么？因为我们是从大到小，前i个既然不是队员的那就是观众，
///观众数量必须小于等于k才说明可以继续放新的观众
dp[i][j]=max(dp[i][j],dp[i-1][j]+s[i].a);///目前第i个人作为观众
else
dp[i][j]=dp[i-1][j];
for(int t=0;t<=p;t++){
if(j&(1<<t)){
dp[i][j]=max(dp[i][j],dp[i-1][j-(1<<t)]+s[i].p[t]);///第i个人作为队员
}
}
}
}
cout<<dp[n][(1<<p)-1]<<"\n";
return 0;
}
D
题意：给你n*n的方格，然后每个格子本来有5个操作分别表示如果你此时在这个格子，就得按照字母进行其中一项操作，上，下，左，右，原地不动，但是现在这些字母不见了，但是你知道的是如果你此时在x，y点，再经过方格上的操作后最终目的地，如果是-1，-1的话说明一直走动停不下来
首先我们可以先在输入的时候对于x=i，y=j，先给存入答案x，因为他们的目的地是本身这个格子嘛，接下来就是其他格子如果没有-1-1，那么他们肯定是会沿着一条路径前往到其他一个点例如a，b停止，也就是这条路径上的点都会是a，b这个目的地坐标，所以我们由第一开始的x点dfs出去，若此时在该点的上面得到和x相同坐标的点，那么此时这个新的点操作肯定是‘D’，表示向下，同时vis标记该点有答案了
那-1，-1这种情况呢？那他肯定是由一个个-1，-1组成个死循环，所以我们反过来，由该点上面得到-1，-1这个新点，那么你此时这个点就是‘U'表示向上，然后再dfs这个新的点；
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
typedef pair<int,int> pp;
const int N=1e3+5;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double pi=acos(-1);
const double eps=1e-6;
mt19937 rnd(time(0));
pp g[N][N];
int vis[N][N];
char ans[N][N];
int dx[4]={1,-1,0,0};
int dy[4]={0,0,-1,1};
char d[4]={'U','D','R','L'};
char fd[4]={'D','U','L','R'};
void dfs(int x,int y)
{
for(int i=0;i<4;i++){
int xx=x+dx[i];
int yy=y+dy[i];
if(vis[xx][yy])continue;
if(g[x][y].first==g[xx][yy].first&&g[x][y].second==g[xx][yy].second)
{
ans[xx][yy]=d[i];
vis[xx][yy]=1;
dfs(xx,yy);
}
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int x,y;
scanf("%d%d",&x,&y);
g[i][j]={x,y};
if(x==i&&y==j)ans[x][y]='X',vis[x][y]=1;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(g[i][j].first==-1){
for(int k=0;k<4;k++){
int x=i,y=j;
int xx=x+dx[k];
int yy=y+dy[k];
if(g[x][y].first==g[xx][yy].first&&g[x][y].second==g[xx][yy].second)
{
ans[x][y]=fd[k];
vis[x][y]=1;
break;
}
}
}
else {
if(ans[i][j]=='X')dfs(i,j);
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(!vis[i][j]){
printf("INVALID\n");
return 0;
}
}
}
printf("VALID\n");
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
printf("%c",ans[i][j]);
}puts("");
}
return 0;
}
C
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair<int, int>
#define mk make_pair
using namespace std;
typedef long long ll;
const int N=1e6+10;
const ll mod=1e9+7;
ll a[N],b[N],n,m,p,ans1,ans2;
ll input(){
ll x=0,f=0;char ch=getchar();
while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return f? -x:x;
}
int main()
{
n=input();
m=input();
p=input();
rep(i,1,n) a[i]=input();
for(int i=1;i<=n;i++)
if(a[i]%p&&ans1==0) ans1=i;
rep(i,1,m) b[i]=input();
for(int i=1;i<=m;i++)
if(b[i]%p&&ans2==0) ans2=i;
printf("%lld\n",ans1+ans2-2);
}
B
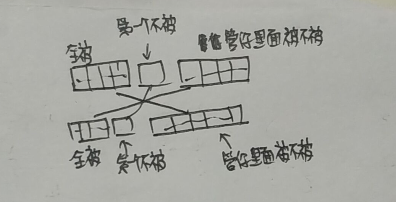
给定一个长度为nn的字符串ss。现规定一种操作。规则如下：
选定一个kk,(1≤k≤n)(1≤k≤n),依次从11开始到n−k+1n−k+1的下标向后截取长度为kk的字符串并将其翻转。问kk取多少可以使得操作后的字符串字典序最小。
会发现其实就是后面的一部分变成新的字符串的前面一串，原字符串的前面变为新字符串的后面部分，同时后面这部分字符串如果k是奇数他还得翻转一次
#include<bits/stdc++.h>
#define maxn 5005
using namespace std;
int T,n;
char str[maxn];
pair<string,int> s[maxn];
int main()
{
scanf("%d",&T);
while(T--)
{
memset(str,0,sizeof(str));
scanf("%d",&n);
scanf("%s",str+1);
for(int i=1;i<=n;++i)
{
string tmp;
for(int j=i;j<=n;++j)tmp.push_back(str[j]);
if((n&1)==(i&1))for(int j=i-1;j>=1;--j)tmp.push_back(str[j]);
else for(int j=1;j<i;++j)tmp.push_back(str[j]);
s[i]=make_pair(tmp,i);
}
sort(s+1,s+n+1);
for(int i=1;i<=n;++i)str[i]=s[1].first[i-1];
printf("%s\n",str+1);
printf("%d\n",s[1].second);
}
}
