codeforces 594

D

给你一个长度为n的括号序列，然后你可以选择交换两个位置，你需要使得能够变成 合法括号序列的起点最多。

题解

1. 人尽皆知的东西：合法的括号序列是，令'('为1，')'为-1，那么前缀和需要>=0，且最后的总和应该为0.

2. 假设现在已经是交换好的序列了，那么答案个数，就是前缀和的最小值的个数。这是因为最小值，例如最小值-1（或者-2），造成这个-1（或者-2）原因就是前面的没有一个1（或者2），那我们就得把前面的-1-2放到后面去，意思就是将最小值的后面第一段作为起点

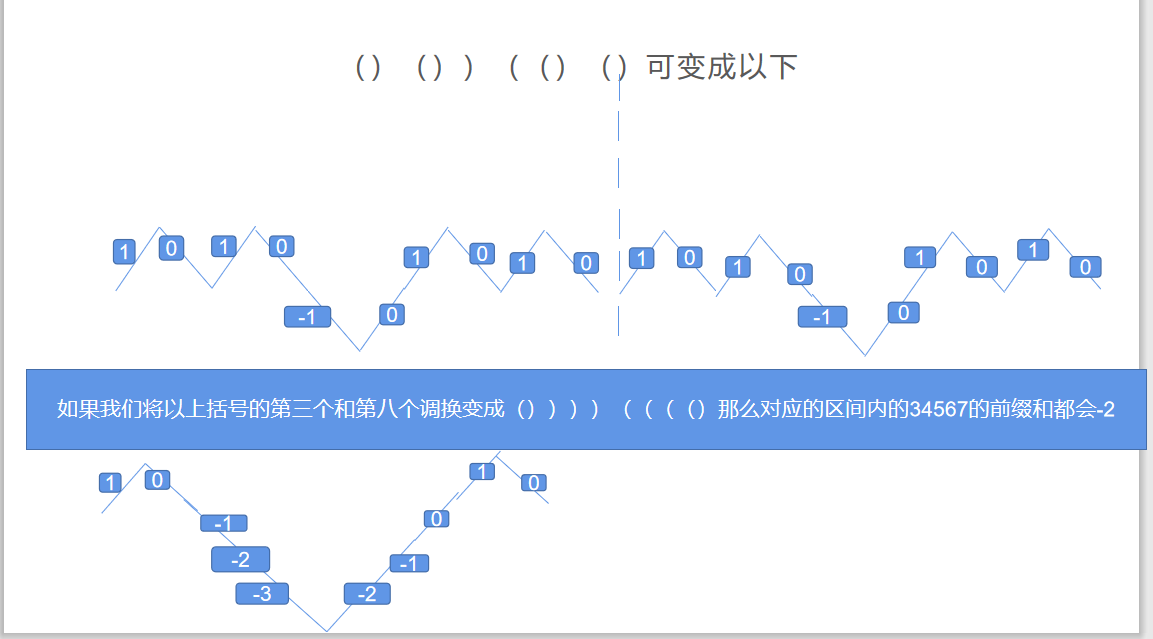
3. 如果交换'('和')'，会使得这个区间的每个数的前缀和-=2，不包括交换点。如果交换')'和'('，你可以改变交换为a[i]和a[j+n]，将其变成交换'('和')'

4. 因为我们使得这个区间里面的每个数都减去了2，那么最小值只可能是 区间内的2+区间外的0，或者区间内的1。

所以我们看两种情况，哪种最小即可

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+7;
int n;
string s;
int a[maxn],ps[maxn];
int main(){
    cin>>n>>s;
    for(int i=0;i<s.size();i++){
        int p = i+1;
        if(s[i]=='('){
            a[p]=a[p+n]=1;
        }else{
            a[p]=a[p+n]=-1;
        }
    }
    for(int i=1;i<=2*n;i++){
        ps[i]=ps[i-1]+a[i];
    }
    if(ps[n]){
        cout<<"0"<<endl;
        cout<<"1 1"<<endl;
        return 0;
    }
    int beg = min_element(ps+1,ps+1+n)-ps;
    int minv = ps[beg];
    for(int i=1;i<=2*n;i++){///所有值减去最小值，也就是最低也是从0开始
        ps[i]-=minv;
    }
    int cl = -1, cc = 0;
    int mx = 0,ansl = 1,ansr = 1;
    int cl2 = 0, cc2 = 0;
    int mx2 = 0, ans2l = 1, ans2r = 1;
    for(int i=1;i<=n;i++){
        if(ps[i+beg]==1){
            if(cc>mx){
                mx=cc;
                ansl=cl,ansr=i;
            }
            cl=i+1;///这是因为我们遇到的是1，而选择位置3和位置8交换影响的是3 4 5 6 7；
            ///所以ans1=i+1；ansr=i；
            cc=0;
        }else if(ps[i+beg]==2)++cc;
    ///上面这部分表示的是区间里全都是大于等于2的这样减2才可以保证最低的值是0；然后再到下面统计区间外的0；
    ///同时第一个2肯定是从1进去，最后一个2肯定碰到1，所以上面的if来判断边界
    
    
        if(ps[i+beg]==0){
            if(cc2>mx2){
                mx2=cc2;
                ans2l=cl2+1,ans2r=i;
            }
            cl2=i;
            cc2=0;
        }else if(ps[i+beg]==1)++cc2;
    }
    for(int i=1;i<=n;i++){
        if(ps[i+beg]==0)++mx;///刚开始懵逼万一有的0是我们区间统计2里面的0怎么办呢，然后想一下哦对哦区间2统计的是区间内全是大于等于2的不可能出现0，所以就是区间全大于等于2的-2变为0后+上区间外的0，和区间内的全为1再-2等于-1的比较
    }
    if(mx2>mx){
        mx=mx2;
        ansl=ans2l;
        ansr=ans2r;
    }
    cout<<mx<<endl;
    cout<<(ansl+beg-1+n)%n+1<<" "<<(ansr+beg-1+n)%n+1<<endl;
}