三分查找
https://www.jianshu.com/p/9e384b4a2588
二分用于单调
三分用于凹凸函数
模板提:
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-6;
double y;
double check(double x){
return pow(x,7)*6+pow(x,6)*8+pow(x,3)*7+pow(x,2)*5-x*y;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%lf",&y);
// cin>>y;
double l,r,midl,midr;
l=0,r=100;
while(r-l>eps){
midl=(l+r)/2;
midr=(midl+r)/2;
if(check(midl)>check(midr)) l=midl;//这里是凹函数所以这样写
else r=midr;
}
printf("%.4f\n",check((r+l)/2));
}
}
light bulb
求人影最长长度:
推导过程如下:(运用2次相似三角形)
1 k/(D+k) = z/H; ---> k = Dz/(H-z)
2 k/(y+k) = z/h; ---> k = zy/(h-z)
So D/(H-z) = y/(h-z) ----解出z----> z = H - (H-h)*D/x
L = z + y ---> L = D-x+H-(H-h)*D/x;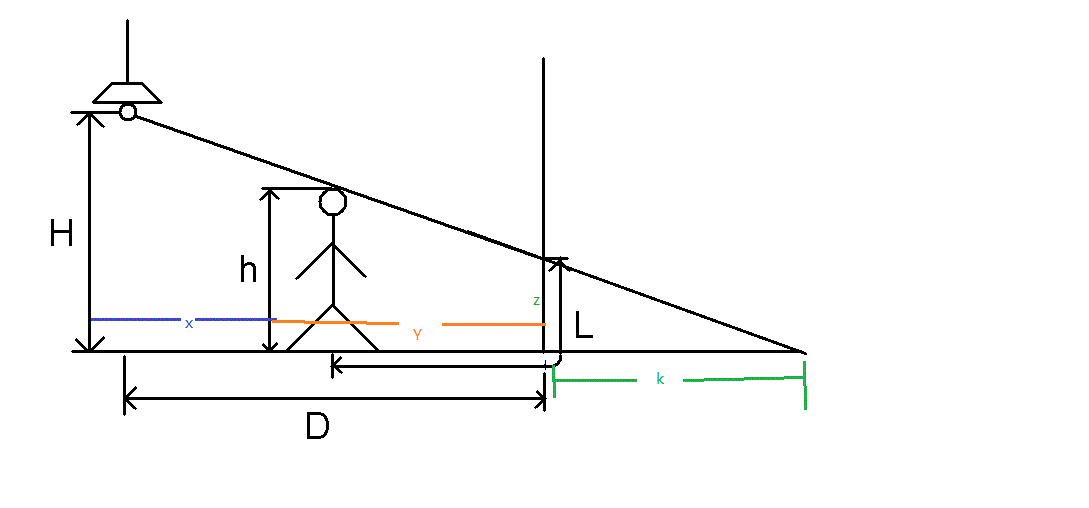
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-9;
double H,h,D;
double check(double x){
return D-x+H-(H-h)*D/x;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%lf%lf%lf",&H,&h,&D);
// cin>>y;
double l,r,midl,midr;
l=(H-h)*D/H,r=D;D*(H-h)/H;//在墙壁上的影子长度为0时,人与灯的距离,l不能等于0,因为这个函数只在这个区间符合函数
while(r-l>=eps){
midl=(l+r)/2;
midr=(midl+r)/2;
if(check(midl)<check(midr)) l=midl;//这里的是凸函数所以这样写
else r=midr;
}
printf("%.3f\n",check((r+l)/2));
}
}
hdu 4717
题意是 给你一个点的方向和速度,求的是随着时间x的增长,你需要找出(任意两个点之间的距离的那个最大值)然后在哪个时刻该最大值最小。
首先我们知道任意两个点之间的距离肯定是要么先减后增,要么递增,然后我们把图画出来,根据题意就是把每个时刻的最高的那个交点连起来,就会发现,这是一个凹函数,直接丢三分查最小值就完事。
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdio>
using namespace std;
double eps=1e-6;
int n; //点的个数
struct mq
{
double x;
double y;
double vx;
double vy;
};
mq node[305];
double dis(mq a,mq b,double t)
{
return sqrt((a.x+a.vx*t-b.x-b.vx*t)*(a.x+a.vx*t-b.x-b.vx*t)+(a.y+a.vy*t-b.y-b.vy*t)*(a.y+a.vy*t-b.y-b.vy*t));
}
double cal(double t)
{
int i,j;
double ans=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
ans=max(ans,dis(node[i],node[j],t));
return ans;
}
int main()
{
int tes,i;
scanf("%d",&tes);
int cas=0;
while(tes--)
{
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%lf%lf%lf%lf",&node[i].x,&node[i].y,&node[i].vx,&node[i].vy);
double left,right,mid,mimid;
left=0,right=10000000;
while(right-left>eps)
{
mid=(left+right)/2.0,mimid=(right+mid)/2.0;
if(cal(mid)<cal(mimid))
right=mimid;
else
left=mid;
}
printf("Case #%d: %.2f %.2f\n",++cas,mid,cal(mid));
}
return 0;
}
POJ3737
题意:给你一个圆锥,圆锥面积给出,问你圆锥的最大体积是多少。
思路:枚举底面圆半径,算圆锥的体积。可以列出表达式,满足三分,因此可以三分枚举底面圆半径。
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
double s,h;
const double pi=acos(-1.0);
{
h=sqrt(pow((s-pi*r*r)/(pi*r),2.0)-r*r);
return pi*r*r*h/3.0;
}
int main()
{
while(scanf("%lf",&s)!=EOF)
{
double left=0.0,right=sqrt(s/(2.0*pi));
double m,mm;
while(left+1e-11<right)
{
m=(left+right)/2.0;
mm=(m+right)/2.0;
if(v(m)>v(mm))right=mm;
else
left=m;
}
printf("%.2lf\n%.2lf\n%.2lf\n",v(left),h,left);
}
return 0;
}
Party All the Time
题意:给出每个精灵在x轴上的坐标,还有自身的重量,接下来这些精灵需要集中到一个点上,不过要产生到目的地的距离的三次方再乘以自身的重量的花费,求最小的花费,我个人眯着眼睛大概想了下整体模型,然后发现这个点肯定是在最左端的那个单位和最右端的端点之间的,拿笔画画也可以看出来,区间外的点靠近区间的时候,花费是越来也越少的。
接下来我们想就知道了从左端点开始往右移动这个点,会发现左端的点不断增加花费,右边的点不断减少花费,假设有超多的点,就可以看出先是单调递减,接下来假设过了一定的点,左边增加的大于减少了,那就是单调递增,所以这是一个凹函数,套三分完事。
///bu'y'xiang
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define EPS 1e-7
#define MAXN 50050
double x[MAXN], w[MAXN];
int n;
double Cal(double pos){
double ans = 0;
for(int i = 1; i <= n; i ++){
double tmp = abs(pos - x[i]);
ans += w[i] * tmp * tmp * tmp;
}
return ans;
}
double Solve(){
double Left, Right;
double mid, midmid;
double mid_value, midmid_value;
Left = x[1];
Right = x[n];
while(Left + EPS < Right){
mid = (Left + Right) / 2;
midmid = (mid + Right) / 2;
mid_value = Cal(mid);
midmid_value = Cal(midmid);
if(mid_value <= midmid_value)
Right = midmid;
else
Left = mid;
}
return Cal(Left);
}
int main(){
int t;
int cnt = 0;
while(~scanf("%d", &t))
{
while(t --){
cnt ++;
scanf("%d", &n);
for(int i = 1; i <= n; i ++){
scanf("%lf %lf", &x[i], &w[i]);
}
printf("Case #%d: %.0lf\n", cnt, Solve());
}
}
return 0;
}
HDU3400
题目大意:
给出两条平行的线段AB, CD,然后一个人在线段AB的A点出发,走向D点,其中,人在线段AB上的速度为P, 在线段CD上的速度为Q,在其他地方的速度为R,求人从A点到D点的最短时间。
题解:
其实就是三分上再三分,怎么理解呢?
首先我们先假设ab上已经找到一个点E,我们要找到另一个点为F,我们发现我们所找的最小值点F满足凹函数,从点F左边过了单调递减,从F往右边去是单调递增。所以我们是可以在假定E找到的时候三分出F的,那么也就可以从F推知E点也是符合三分的
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
const double eps = 1e-8;
using namespace std;
struct point
{
double x,y;
}a,b,c,d;
double v1,v2,v0;
double ax,ay,bx,by,cx,cy,dx,dy;
double dis(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double f(point x)
{
double t1,t2;
point l,r,m1,m2;
l=c,r=d;
do
{
m1.x=(l.x+r.x)/2;
m1.y=(l.y+r.y)/2;
m2.x=(m1.x+r.x)/2;
m2.y=(m1.y+r.y)/2;
t1=dis(m1,x)/v0+dis(m1,d)/v2;
t2=dis(m2,x)/v0+dis(m2,d)/v2;
if(t1>t2) l=m1;
else r=m2;
}while(dis(l,r)>=eps);
return t1;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y>>d.x>>d.y;
cin>>v1>>v2>>v0;
point l,r,m1,m2;
double t1,t2;
l=a;r=b;
do
{
m1.x=(l.x+r.x)/2;
m1.y=(l.y+r.y)/2;
m2.x=(m1.x+r.x)/2;
m2.y=(m1.y+r.y)/2;
t1=dis(m1,a)/v1+f(m1);
t2=dis(m2,a)/v1+f(m2);
if(t1>t2) l=m1;
else r=m2;
}while(dis(l,r)>=eps);
printf("%.2lf\n",t1);
}
return 0;
}
HDU2438:Turn the corner(三分)
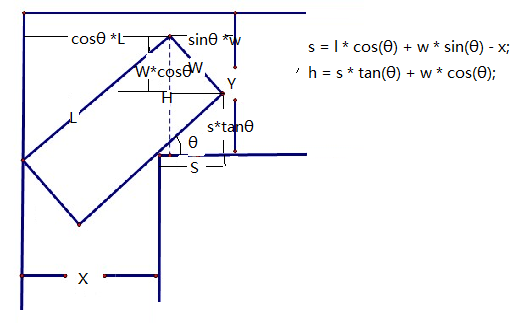
题意,给出x,y,l(车长),w(车头),求从x过来的时候,能不能成功转弯过到y。
根据这张图,我们只要使得h<=y即可,可以发现h是一个凸函数,故使用三分,具体见代码
牛客网:
https://ac.nowcoder.com/acm/contest/3006/B
#include <bits/stdc++.h>
using namespace std;
double eps=1e-8;
struct p{
int x,y;
}a[100005];
int n;
double check(double x)
{
double max=0;
for (int i=1;i<=n;i++)
{
double tmp=sqrt(a[i].y*a[i].y+(a[i].x-x)*(a[i].x-x));
if (tmp>max) max=tmp;
}
return max;
}
double tsearch(double left,double right){
int i;
double mid,midmid;
while(right-left>eps){
mid=(left+right)/2.0;
midmid=(mid+right)/2.0;
if(check(mid)>check(midmid)) //极大值求法
left=mid;
else
right=midmid;
}
return mid;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y);
double max=tsearch(-10000,10000);
printf("%.4lf\n",check(max));
return 0;
}
二分
Drying POJ - 3104
题意:有n件衣服,若自然风干,则每分钟减少1单位水,若烘干,每分钟减少k单位水(烘干时不再考虑自然风对其影响),每次只能选取一件衣服进行烘干,问最少需要多长时间将所有衣服烘干。
思路:通过二分查找,mid为我们尝试的答案,当k=1是,答案应该为数组里的最大值。当k!=1时,我们可以发现,比mid小或等于mid的衣服可以直接忽略,因为这些衣服可以自然干,剩下的衣服也可以都减去mid,然后将剩下的也就是b[i]与k进行运算,计算出需要多少时间。计算公式的推出:设将一件衣服弄干,共需要x分钟,设烘干的时间为y,则自然干的时间为(x-y),将衣服弄干的条件即为k*y+(x-y)>= a [i],化简为:y*(k-1)+x >= a[i],因此y = (a[i]-x)/(k-1)。
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std;
#define MAXN 100000+10
#define LL long long
int n, k;
int wat[MAXN];
bool Judge(int x)
{
LL t = 0;
for (int i = 0; i<n; i++)
{
if (wat[i]>x)
{
int xx = ceil((wat[i] - x)*1.0 / (k - 1));
t += xx;
}
if (t>x)return false;
}
if (t>x)return false;
else return true;
}
int main()
{
while (~scanf("%d", &n))
{
int l = 1, r = 0;
for (int i = 0; i<n; i++)
{
scanf("%d", &wat[i]);
r = max(r, wat[i]);
}
scanf("%d", &k);
if (k == 1)
{
printf("%d\n", r);
continue;
}
int mid = 0;
while (l <= r)
{
mid = (l + r) / 2;
if (Judge(mid))
{
r = mid - 1;
}
else
l = mid + 1;
}
printf("%d\n",l);
}
return 0;
}



