cf rock is push 【dp】
附上学习的博客：https://blog.csdn.net/u013534123/article/details/102762673
大致题意：一个迷宫，里面有很多箱子，你可以向右或者向下走。当你遇到一个或者多个箱子的时候，你可以把箱子往你移动的方向推动，但是不能把箱子推出到墙壁外面。你从左上角出发，问你有多少种方法到右下角。
考虑如果没有箱子，那么就是一个很简单的递推问题，对于一个格子，要么从上面要么从左边来。有箱子的话，由于箱子可以被推动而且不能推到外面，所以我们要考虑是否可以从上面或者下面过来。
还是一样考虑dp，令dp[i][j][0]表示走到位置(i,j)且最后一步是从左边过来的方案，同理dp[i][j][1]表示最后一步从上面来的方案数。然后转移的话，考虑如果是从上面来，我们可以枚举最后一次向右走的位置k，即从(k,j)到(i,j)是一直往下走。如此我们只需要判断是否可以走过来，也即判断(k,j)往下的石头数目是否大于(i,j)下方的格子数，如果大于，那么说明是可以走到(i,j)的，那么把方案数dp[k][j][0]。同理可以得出从左边来，方案数就是dp[i][k][1]。于是有转移方程：
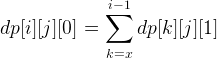
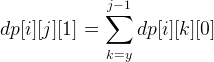
x和y分别表示最前的一个位置，且从这个位置开始到那一行或者那一列的最后的石头数目小于等于后面允许放石头的格子数目。x和y可以用二分比较快速的求，然后显然可以用前缀和来优化，于是复杂度就是O(N^2logN)。然后，仔细想想可以发现x和y是有单调性的，于是可以进一步优化到O(N^2)，但是考虑到并没有这个必要而且会复杂一点所以我就没有写了。具体见代码：
——————以上是博客的解法
我另外补充下：
#include<bits/stdc++.h>
#define fi first
#define se second
#define LL long long
#define pb push_back
#define INF 0x3f3f3f3f
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;
const int N = 2010;
const int mod = 1e9 + 7;
int dp[N][N][2],sum[N][N][2],R[N][N][2];
char s[N][N];
int main()
{
int n,m;
scc(n,m);
if(n==1&&m==1)
{
puts("1");
return 0;
}
for(int i=0;i<n;i++)
{
scanf("%s",s[i]);
for(int j=0;s[i][j];j++)
if (s[i][j]=='R') R[i][j][0]=R[i][j][1]=1;
}
for(int i=0;i<n;i++)
for(int j=1;j<m;j++)
R[i][j][0]+=R[i][j-1][0];//前缀和表示到列到该点的石头
for(int i=0;i<m;i++)
for(int j=1;j<n;j++)
R[j][i][1]+=R[j-1][i][1];
sum[0][0][0]=sum[0][0][0]=1;
dp[0][0][0]=dp[0][0][1]=1;
for(int i=1;i<n;i++)
{
if (R[n-1][0][1]<=n-i-1) //因为石头只能推到边不能出界，例如该列五个格子有两个格子有石头，那你肯定有效格数到3这一个嘛
dp[i][0][1]+=dp[i-1][0][1];
sum[i][0][0]=dp[i][0][1];//为什么sum的第三维是0呢？请看上图公式
}
for(int i=1;i<m;i++)
{
if (R[0][m-1][0]<=m-i-1)
dp[0][i][0]+=dp[0][i-1][0];
sum[0][i][1]=dp[0][i][0];
}
for(int i=1;i<n;i++)
for(int j=1;j<m;j++)
{
int l=0,r=i-1,mid,t,res=-1;
while(l<=r)//二分找找到第某行，该行小于等于后面允许放石头的格子数目
{
mid=l+r>>1;
t=R[n-1][j][1]-R[mid][j][1];
if (t<=n-i-1) res=mid,r=mid-1;
else l=mid+1;
}
if(res>=0)
{
int tmp=res==0?0:sum[res-1][j][1];
dp[i][j][1]=(sum[i-1][j][1]-tmp+mod)%mod;//前缀和基操，
}
sum[i][jd][0]=(sum[i][j-1][0]+dp[i][j][1])%mod;
l=0,r=j-1,res=-1;
while(l<=r)
{
mid=l+r>>1;
t=R[i][m-1][0]-R[i][mid][0];
if (t<=m-j-1) res=mid,r=mid-1;
else l=mid+1;
}
if (res>=0)
{
int tmp=res==0?0:sum[i][res-1][0];
dp[i][j][0]=(sum[i][j-1][0]-tmp+mod)%mod;
}
sum[i][j][1]=(sum[i-1][j][1]+dp[i][j][0])%mod;
}
printf("%d\n",(dp[n-1][m-1][0]+dp[n-1][m-1][1])%mod);
}
