点分治开始!
放下学习的博客:https://www.cnblogs.com/bztMinamoto/p/9489473.html
首先介绍下点分治,例如我们求路径,路径就是点与点间的,然后路径就两种情况经过该点的路径于不经过该点的路径,所以
我们以一个点开始开始dfs,找出所又路径两辆合并什么的,之后这个点就得删掉了,那接下来树就被分割成两个了,也就是我们的分治就是不断将一棵树分成好几颗小的树。
但是如果是一条链呢?那按我们上门说的,直接爆炸,n的平方复杂度,所以接下来我们引入重心,保持复杂度
实际上,一棵树的最大子树最小的点有一个名称,叫做重心。
暴力求重点
void findrt(int u,int fa){
//sz表示子树的大小,son表示点的最大子树的大小
//cmax(a,b)表示如果b>a则a=b
//个人习惯这样写,或者直接写成a=max(a,b)
sz[u]=1,son[u]=0;
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(vis[v]||v==fa) continue;
findrt(v,u);
sz[u]+=sz[v];
cmax(son[u],sz[v]);
}
//size表示整棵树的大小
//因为这是一棵无根树,所以包括它的父亲在内的那一坨也应该算作它的子树
cmax(son[u],size-sz[u]);
if(son[u]<mx) mx=son[u],rt=u;
}
合并的时候有个小问题,先给代码
void divide(int u){
ans+=solve(u,0);
vis[u]=1;
int totsz=size;
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(vis[v]) continue;
ans-=solve(v,edge[i]);
mx=inf,rt=0;
size=sz[v]>sz[u]?totsz-sz[u]:sz[v];//这里应该这样写才是对的
findrt(v,0);
divide(rt);
}
}
上面其他的应该都好理解,除了这一句 ans-=solve(v,edge[i]);
考虑一下这棵树
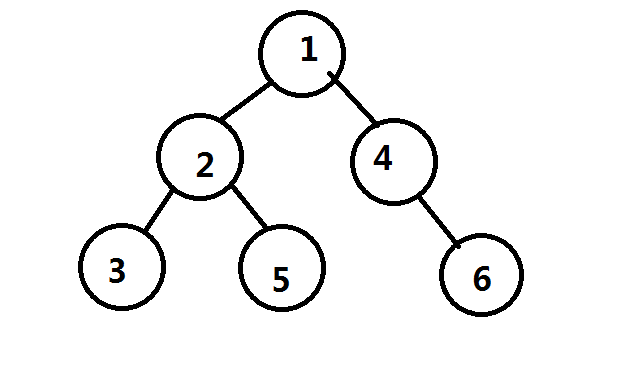
考虑一下,从点11出发的路径有以下几条
1−>41−>4
1−>4−>61−>4−>6
1−>21−>2
1−>2−>31−>2−>3
1−>2−>51−>2−>5
然后我们为了求贡献,会将路径两两合并
然而合并1−>2−>31−>2−>3和1−>2−>51−>2−>5这两条路径实际上是不合法的,因为出现了重边
所以要减去22这一棵子树中的所有路径两两合并的贡献
然后回头来看代码 ans+=solve(u,0); ans-=solve(v,edge[i]);
看到没?第二个参数不一样,这样在考虑子树中两两合并时的贡献时就不会把这一条边的贡献给漏掉了
然后只要递归继续找就可以(*^▽^*)。
然后接下来第一道题:
poj1741tree
给一颗n个节点的树,每条边上有一个距离v。定义d(u,v)为u到v的最小距离。给定k值,求有多少点对(u,v)使u到v的距离小于等于k。
点分的板子……好像基本都是板子套进去……就是注意合并的时候二分保证复杂度
#include <cstdio>
#include <algorithm>
#define N 40005
#define M 80005
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<15,stdin),p1==p2)?EOF:*p1++)
char buf[1<<15],*p1=buf,*p2=buf;
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0'; c=getchar();}
return x*f;
}
int ver[M],Next[M],head[N],edge[M];
int n,tot,root;ll k;
void add(int u,int v,int e){
ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;
ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e;
}
int sz[N],vis[N],mx,size;
ll d[N],q[N],l,r;
void getroot(int u,int fa){
sz[u]=1;int num=0;
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(v==fa||vis[v]) continue;
getroot(v,u);
sz[u]+=sz[v];
cmax(num,sz[v]);
}
cmax(num,size-sz[u]);
if(num<mx) mx=num,root=u;
}
void getdis(int u,int fa){
q[++r]=d[u];
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(v==fa||vis[v]) continue;
d[v]=d[u]+edge[i];
getdis(v,u);
}
}
ll calc(int u,int val){
r=0;
d[u]=val;
getdis(u,0);
ll sum=0;l=1;
sort(q+1,q+r+1);
while(l<r){
if(q[l]+q[r]<=k) sum+=r-l,++l;
else --r;
}
return sum;
}
ll ans=0;
void dfs(int u){
ans+=calc(u,0);
vis[u]=1;
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(vis[v]) continue;
ans-=calc(v,edge[i]);
size=sz[v];
mx=inf;
getroot(v,0);
dfs(root);
}
}
int main(){
//freopen("testdata.in","r",stdin);
while(1){
n=read();k=read();
if(n==0&&k==0) break;
for(int i=1;i<n;++i){
int u=read(),v=read(),e=read();
add(u,v,e);
}
size=n;
mx=inf;
getroot(1,0);
dfs(root);
printf("%lld\n",ans);
ans=tot=0;
for(int i=1;i<=n;i++)
head[i]=vis[i]=sz[i]=q[i]=d[i]=0;
}
return 0;
}
第二:luogu 3806
这道题如果直接按上面做法然后双for来更新答案(例如博客那样)
肯定是不行的n平方不是有病嘛
所以我们换一下,依然二分更新答案
calc函数和get_dis函数不一样,其他都差不多
aa数组记录从root能到的点
dd数组记录a_{i}ai到root的距离
bb数组记录a_{i}ai属于root的哪一棵子树(即当b[a[i]]==b[a[j]]时,说明a[i]与a[j]属于root的同一棵子树)
注意:将a数组排序时应按照d值的大小:
cmp函数:
bool cmp(int x,int y){
return d[x]<d[y];
}#include<bits/stdc++.h>
using namespace std;
const int M=10001;
const int inf=0x3f3f3f3f;
struct node{int nxt,edg,to;}h[M*2];
int cnt,n,m,query[M],vis[M],b[M],q[M],d[M],ok[M],maxx,sze,sz[M],tot,head[M],root;
bool cmp(int x,int y)
{
return d[x]<d[y];
}
void add(int u,int v,int e)
{
h[++tot].to=v,h[tot].nxt=head[u],head[u]=tot;h[tot].edg=e;
}
void getroot(int u,int fa)
{
sz[u]=1;
int num=0;
for(int i=head[u];i;i=h[i].nxt){
int v=h[i].to;
if(v==fa||vis[v]) continue;
getroot(v,u);
sz[u]+=sz[v];
num=max(num,sz[v]);
}
num=max(num,sze-sz[u]);
if(num<maxx) maxx=num,root=u;
// printf("root=%d\n",root);
}
void getdis(int u,int fa,int dis,int from)
{
q[++cnt]=u;
d[u]=dis;
b[u]=from;
for(int i=head[u];i;i=h[i].nxt)
{
int v=h[i].to;
if(v==fa||vis[v]) continue;
getdis(v,u,h[i].edg+dis,from);
}
}
void cal(int u)
{
cnt=0;
q[++cnt]=u,d[u]=0,b[u]=u;
for(int i=head[u];i;i=h[i].nxt){
int v=h[i].to;
if(vis[v])continue;
getdis(v,u,h[i].edg,v);
}
sort(q+1,q+cnt+1,cmp);
// for(int i=1;i<=cnt+1;i++) printf("q=%d ",q[i]);puts("");
for(int i=1;i<=m;i++){
int l=1,r=cnt;
if(ok[i]) continue;
while(l<r){
if(d[q[l]]+d[q[r]]>query[i]) r--;//长度大于k,r--
else if(d[q[l]]+d[q[r]]<query[i]) l++;//长度小于k,l++
else if(b[q[l]]==b[q[r]]){if(d[q[r]]==d[q[r-1]])r--;else l++;}//长度等于k了但是很遗憾在同一颗紫薯里,也就是他们有公共边,那抱歉如果右边-1的那位可以继续保持,那就r--让他来,因为现在已经是正确答案了,如果不是那只能l++来继续了
else{ok[i]=1;break;}///通过前面三重关卡恭喜你得到了这条路径
}
}
}
void dfs(int u)
{
vis[u]=1;
cal(u);
for(int i=head[u];i;i=h[i].nxt)
{
int v=h[i].to;
if(vis[v]) continue;
sze=sz[v];
maxx=inf;
getroot(v,0);
dfs(root);
}
}
int main()
{
int u,v,e;
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
scanf("%d%d%d",&u,&v,&e);
add(u,v,e);add(v,u,e);
}
for(int i=1;i<=m;i++) scanf("%d",&query[i]);
sze=n;
maxx=inf;
getroot(1,0);
dfs(root);
for(int i=1;i<=m;i++)
{
if(ok[i]) cout<<"AYE"<<endl;
else cout<<"NAY"<<endl;
}
}
//理解一下:重心就是它可以很好的分割子树,
//然后我们因为如果只是按原来的树那样的公式递归下去找儿子,
//如果出现一条链,直接爆炸,这种递归子树下去我们可以联想到的是点分治啦,
//但是你要知道,所以我们点分树和原树不同的,所以我们只需要对新的一颗点分树进行维护新信息
//我们知道每个重点负责着一颗小子树,所以按题解那样维护,所以每次比较重心,以及改重心原树中的临界点,
//我们这些点进行比较是以该点为重心时的子树的,所以更优就进该点所在子树的重心里,因为你的这个所求的带权重点一定在次子树里面,
//我们就是以防他是一条链直接爆炸,故进入该子树的重心来进行递归。还有就是为什么更新的时候一个一个往上暴力找父亲呢,
//因为我们的重心是第一层连第二层连第三层,也就是第三层的重心实际上会被包含在第二层重心的子树里的,显然的,所以我们更新一个点,同样如此持续爬上子分树上的父亲更新
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
template<typename T>inline void read(T &num){
char ch; int flg = 1;
while((ch=getchar())<'0'||ch>'9')if(ch=='-')flg=-flg;
for(num=0;ch>='0'&&ch<='9';num=num*10+ch-'0',ch=getchar());
num*=flg;
}
const int MAXN = 100005;
int n, q, fir[MAXN], cnt;
struct edge { int to, nxt, w; }e[MAXN<<1];
inline void add(int u, int v, int wt) {
e[cnt] = (edge){ v, fir[u], wt }, fir[u] = cnt++;
e[cnt] = (edge){ u, fir[v], wt }, fir[v] = cnt++;
}
int dis[MAXN], son[MAXN], sz[MAXN], top[MAXN], fa[MAXN], dep[MAXN];
void dfs(int u, int ff) {
dep[u] = dep[fa[u]=ff] + (sz[u]=1);
for(int i = fir[u], v; ~i; i = e[i].nxt)
if((v=e[i].to) != ff) {
dis[v] = dis[u] + e[i].w;
dfs(v, u), sz[u] += sz[v];
if(sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp;
if(son[u]) dfs2(son[u], tp);
for(int i = fir[u], v; ~i; i = e[i].nxt)
if((v=e[i].to) != fa[u] && v != son[u])
dfs2(v, v);
}
int lca(int u, int v) { //
while(top[u] != top[v]) {
if(dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
int dist(int u, int v) { return dis[u] + dis[v] - 2*dis[lca(u,v)]; }
int Fa[MAXN], size[MAXN], Size, Minr, root, info[MAXN], CNT;
struct EDGE { int to, nxt, rt; }E[MAXN];
inline void ADD(int u, int v, int rr) {
E[CNT] = (EDGE){ v, info[u], rr }, info[u] = CNT++;
}
bool vis[MAXN];
void Getrt(int u, int ff) {
size[u] = 1;
int ret = 0;
for(int i = fir[u], v; ~i; i = e[i].nxt)
if((v=e[i].to) != ff && !vis[v]) {
Getrt(v, u), size[u] += size[v];
ret = max(ret, size[v]);
}
ret = max(ret, Size-size[u]);
if(ret < Minr) Minr = ret, root = u;
}
void DFS(int u, int ff) {
vis[u] = 1; Fa[u] = ff;
for(int i = fir[u], v; ~i; i = e[i].nxt)
if(!vis[v=e[i].to]) {
Minr = n; Size = size[v];
Getrt(v, u);
ADD(u, v, root);
DFS(root, u);
}
}
LL sum[MAXN]; //子树点数之和
LL sumd[MAXN]; //子树内的距离之和
LL sumf[MAXN]; //子树对父亲的贡献
inline void Modify(int u, int val) {
sum[u] += val;
for(int i = u; Fa[i]; i = Fa[i]) {
int len = dist(u, Fa[i]);
sum[Fa[i]] += val;
sumd[Fa[i]] += 1ll * val * len;
sumf[i] += 1ll * val * len;
}
}
inline LL Count(int u) { //多理解一会,画画图多YY下
LL res = sumd[u]; //自己子树的距离之和
for(int i = u; Fa[i]; i = Fa[i]) {
int len = dist(u, Fa[i]);
res += (sum[Fa[i]]-sum[i]) * len; //Fa[i]的其他子树额外的点数 * 这一条边
res += (sumd[Fa[i]]-sumf[i]); //Fa[i]的其他子树的点到Fa[i]的距离之和
//上面两个统计都必须要减去这个子树的贡献,否则算重了
}
return res;
}
LL Query(int u) {
LL tmp = Count(u);
for(int i = info[u]; ~i; i = E[i].nxt)
if(Count(E[i].to) < tmp) return Query(E[i].rt); //儿子比自己优就去对应的重心
return tmp;
}
int main () {
memset(fir, -1, sizeof fir);
memset(info, -1, sizeof info);
read(n), read(q);
for(int i = 1, x, y, z; i < n; ++i)
read(x), read(y), read(z), add(x, y, z);
dfs(1, 0), dfs2(1, 1);
Size = Minr = n; Getrt(1, 0); //先求一次重心
int RT = root; //作为根
DFS(root, 0);
int x, y;
while(q--) {
read(x), read(y);
Modify(x, y);
printf("%lld\n", Query(RT));
}顺便附上链接:https://www.luogu.org/problemnew/solution/P3345?page=2
}顺便说下:我觉得这篇里的rmq查询lca比较容易看懂,以后就套这个嘻嘻:https://www.cnblogs.com/bztMinamoto/p/9489473.html
接下来一篇luogu的开店:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#define ll long long
#define N 150005
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
inline int read(){
#define num ch-'0'
char ch;bool flag=0;int res;
while(!isdigit(ch=getc()))
(ch=='-')&&(flag=true);
for(res=num;isdigit(ch=getc());res=res*10+num);
(flag)&&(res=-res);
#undef num
return res;
}
char sr[1<<21],z[20];int C=-1,Z;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
inline void print(ll x){
if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
int head[N],Next[N<<1],ver[N<<1],edge[N<<1];
int n,tot,val[N],q,maxn;
int st[N<<1][19],d[N],dfn[N],num,bin[25],tp,logn[N<<1];
inline void add(int u,int v,int e){
ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;
ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e;
}
inline void ST(){
for(int j=1;j<=tp;++j)
for(int i=1;i+bin[j]-1<=(n<<1);++i)
st[i][j]=min(st[i][j-1],st[i+bin[j-1]][j-1]);
}
void dfs1(int u,int fa){
st[dfn[u]=++num][0]=d[u];
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(v==fa) continue;
d[v]=d[u]+edge[i],dfs1(v,u),st[++num][0]=d[u];
}
}
int fa[N],sz[N],son[N],size,rt;bool vis[N];
void dfs2(int u,int fa){
sz[u]=1,son[u]=0;
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(vis[v]||v==fa) continue;
dfs2(v,u),sz[u]+=sz[v],cmax(son[u],sz[v]);
}
cmax(son[u],size-sz[u]);
if(son[u]<son[rt]) rt=u;
}
inline ll dis(int a,int b){
if(dfn[a]>dfn[b]) a^=b^=a^=b;
int k=logn[dfn[b]-dfn[a]+1];
return d[a]+d[b]-(min(st[dfn[a]][k],st[dfn[b]-bin[k]+1][k])<<1);
}
struct node{
int val;ll sz[3];
node(int a=0,ll b=0,ll c=0,ll d=0){val=a,sz[0]=b,sz[1]=c,sz[2]=d;}
inline bool operator <(const node &b)const
{return val<b.val;}
};
vector<node> sta[N];
void dfs3(int u,int f,int rt){
sta[rt].push_back(node(val[u],1,dis(u,rt),fa[rt]?dis(u,fa[rt]):0));
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(v==f||vis[v]) continue;
dfs3(v,u,rt);
}
}
void dfs4(int u){
vis[u]=true;
dfs3(u,0,u);sta[u].push_back(node(-1,0,0,0));
sort(sta[u].begin(),sta[u].end());
for(int i=0,j=sta[u].size();i<j-1;++i)
sta[u][i+1].sz[0]+=sta[u][i].sz[0],
sta[u][i+1].sz[1]+=sta[u][i].sz[1],
sta[u][i+1].sz[2]+=sta[u][i].sz[2];
for(int i=head[u];i;i=Next[i]){
int v=ver[i];
if(vis[v]) continue;
rt=0,size=sz[v];
dfs2(v,0),fa[rt]=u,dfs4(rt);
}
}
inline node query(int id,int l,int r){
if(id==0) return node();
vector<node>::iterator it1=upper_bound(sta[id].begin(),sta[id].end(),node(r,0,0,0));--it1;
vector<node>::iterator it2=upper_bound(sta[id].begin(),sta[id].end(),node(l-1,0,0,0));--it2;
return node(0,it1->sz[0]-it2->sz[0],it1->sz[1]-it2->sz[1],it1->sz[2]-it2->sz[2]);
}
inline ll calc(int u,int l,int r){
ll res=0;
for(int p=u;p;p=fa[p]){
node a=query(p,l,r);
res+=a.sz[1];
if(p!=u) res+=a.sz[0]*dis(p,u);
if(fa[p]) res-=a.sz[2]+a.sz[0]*dis(fa[p],u);
}
return res;
}
int main(){
ll ans=0;
n=read(),q=read(),maxn=read();
bin[0]=1,logn[0]=-1;
for(int i=1;i<=20;++i) bin[i]=bin[i-1]<<1;
while(bin[tp+1]<=(n<<1)) ++tp;
for(int i=1;i<=(n<<1);++i) logn[i]=logn[i>>1]+1;
for(int i=1;i<=n;++i) val[i]=read();
for(int i=1;i<n;++i){
int u=read(),v=read(),e=read();
add(u,v,e);
}
dfs1(1,0),ST();
rt=0,son[0]=n+1,size=n,dfs2(1,0);
dfs4(rt);
while(q--){
int a=read(),b=read(),c=read();
b=(b+ans)%maxn,c=(c+ans)%maxn;
if(b>c) b^=c^=b^=c;
print(ans=calc(a,b,c));
}
Ot();
return 0;
}




