主成分分析PCA（1）

参考：https://mp.weixin.qq.com/s/6xsXjUEUm8dB5y6-dInT_w

 

PCA的数学原理无非一句话： 协方差矩阵的特征值分解 （或者等价地） 原矩阵的奇异值分解

 

1、PCA：通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

2、数据的向量表示

假设淘宝每天的交易记录为（浏览量, 访客数, 下单数, 成交数, 成交金额），向量表示如下：

$$(500,240, 25, 13, 2312.15)^T$$　　//一般表示为列向量

3、降维：降维意味着信息的丢失，需要利用实际数据中存在的相关性，在降维的同时尽量减少信息损失

例如：浏览量”和“访客数”往往具有较强的相关关系，而“下单数”和“成交数”也具有较强的相关关系

4、内积：将两个向量映射为一个实数

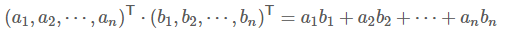
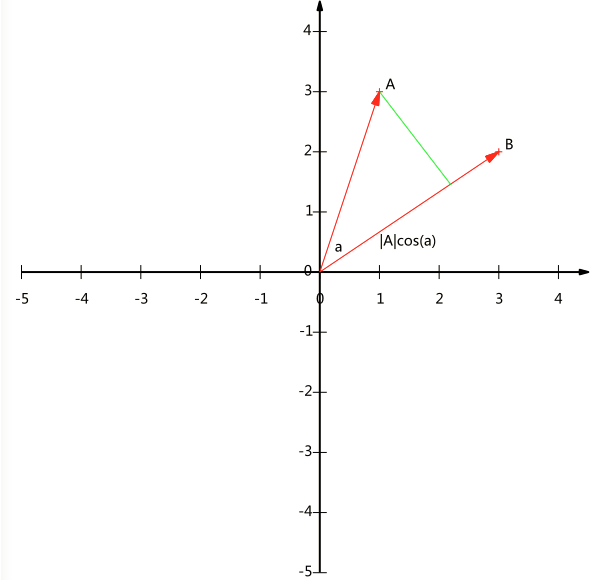
假设$A=(x_1,y_1), B=(x_2, y_2)$，$A$和$B$的夹角为$a$，则$A$在$B$上的投影长度为$|A|\cos(a)$，$A$的模为$|A|=\sqrt{x_1^2+y_1^2}$如图：

同时内积可以表示为$A\cdot B=|A||B|\cos(a)$　　//A与B的内积等于A到B的投影长度乘以B的模

假设令$B$的模为1，则可得：$A\cdot B=|A|\cos(a)$

因此，当$B$的模为1时，内积的一种几何解释为：$A$向$B$所在直线投影的矢量长度！

5、基：要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值　　//通常默认选择$(1,0)^T$和$(0,1)^T$为一组基

因此，想要获得向量在新基上的坐标，只需要分别计算向量与基的内积值即可　　//注：需要基的模为1

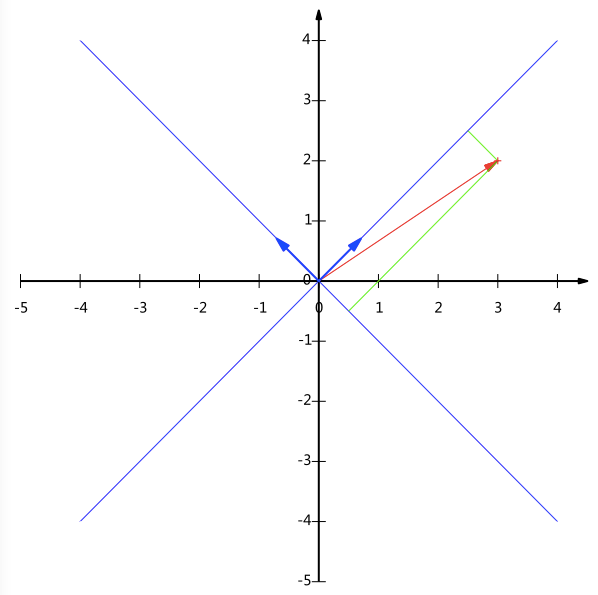
如求解向量$(3, 2)^T$（隐含基为$(1,0)^T$和$(0,1)^T$）在新基$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$和$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$下的坐标　　//注：新基为$(1,1)^T$和$(-1,1)^T$对应的单位基

 结果可表示为矩阵和向量的乘法：

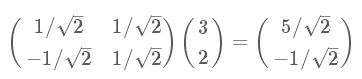
其中，矩阵的行向量为对应的新基

可以将上式进一步推广到多个向量，如将$(1,1)^T$、$(2,2)^T$和$(3,3)^T$变换到新基上：

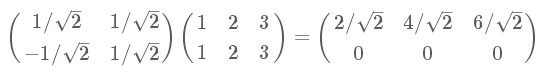
结论：如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果：

其中，$p_i$表示第$i$个基对应的行向量，$a_j$表示第$j$个原始数据向量

注：新基的个数$R$决定了变换后数据的维度，当$R<N$时，此时的矩阵乘法表示降维变换

矩阵乘法的物理解释：将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去　　//矩阵代表基变换

 6、如何选择最优的新基，使得降维后的信息损失最小

假设存在五个数据向量：

（1）预处理

对每个字段去均值（行操作）：

图示如下：

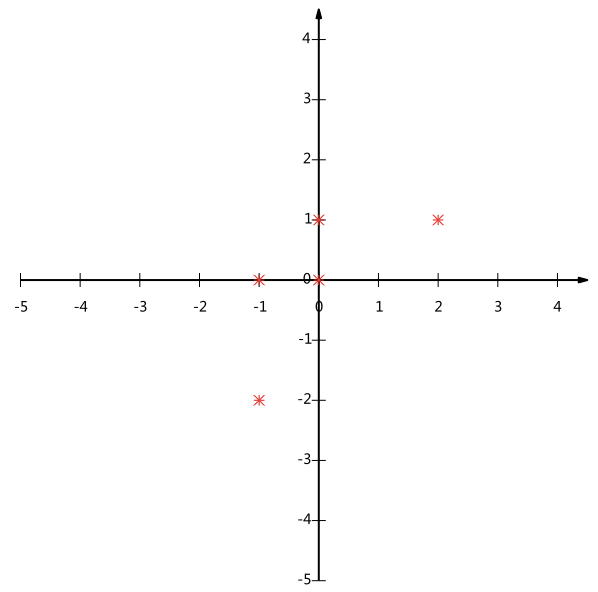
现在的问题是：如何选择一个方向（基），将所有数据都投影到这个方向所在直线上，同时尽量保留最多的原始信息？

一种思路：希望投影后的投影值尽可能分散

（2）方差：描述数据的分散程度

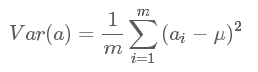
由于已经去均值化：

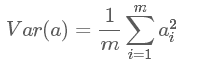
可以看出，在已去均值的情况下，字段的方差与元素自身的内积相关

因此，问题转化为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大

（3）协方差：不同字段的协方差表示其相关性

注：对于超过二维的高维数据，需要保证不同字段之间尽量不存在（线性）相关性　　//相关表示不独立，则存在重复信息

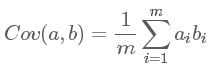可以看出，在已去均值的情况下，不同字段的协方差与元素间的内积相关

当协方差为0时，表示两个字段完全独立。为了让协方差为0，我们选择第二个基时只能在与第一个基正交的方向上选择　　//保证不同方向的正交性

因此，降维问题的优化目标为：将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）

（4）协方差矩阵

假设仅有两个字段$a$和$b$，按行组成矩阵（每一行已去均值）：

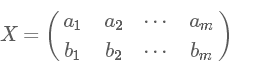
可得协方差矩阵：

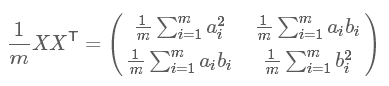
因此：假设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，则矩阵$C=\frac{1}{m}XX^T$是一个对称矩阵，其对角线分别个各个字段的方差，而第$i$行$j$列和$j$行$i$列元素相同，表示$i$和$j$两个字段的协方差

 （5）协方差矩阵对角化　　//协方差矩阵为实对称矩阵

根据（3）中的结论，我们需要将原始数据的协方差矩阵对角化（除对角线以外其他元素全为0，且方差由大至小排列）

假设原始数据矩阵为$X$，对应的协方差矩阵为$C$，$P$为新基作为行向量组成的矩阵，则变换后的数据矩阵为$Y=PX$，则其协方差矩阵$D$为：

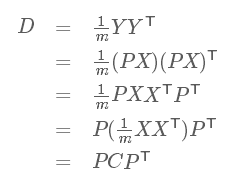
因此，优化目标即为寻找矩阵$P$，使得$PCP^T$为对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

注：在线性代数中，$n$行$n$列的实对称矩阵一定可以找到$n$个单位正交特征向量，设这$n$个特征向量为$e_1, e_2, \cdots , e_n$，我们将其按列组成矩阵：

则对于实对称的协方差矩阵$C$有如下等式成立

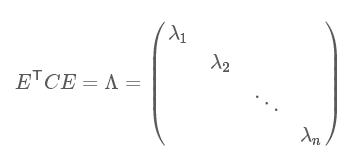
其中，$\Lambda$为对角矩阵，对角元素为各特征向量对应的特征值（可能有重复）

因此，目标矩阵即为$P=E^T$，即协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是$C$的一个特征向量

7、PCA算法步骤：

假设有$m$条$n$维数据

1）将原始数据按列组成$n$行$m$列矩阵$X$

2）将$X$的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵$C=\frac{1}{m}XX^T$

4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量单位化后，按对应特征值大小从上到下按行排列成矩阵，取前$k$行组成矩阵$P$

6）$Y=PX$即为降维到$k$维后的数据

 

注：PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。