线性代数的本质(Essense of Linear Algebra)——3Blue1Brown
视频资料:https://www.bilibili.com/video/av6731067
一、向量是什么
- 物理专业:向量是空间中的箭头,由长度和方向决定
- 计算机专业:向量是有序的数字列表
- 数学家:向量可以是任何东西,只要保证向量相加、数字与向量的相乘有意义即可
(1)当在坐标系下以有序多元数组的形式表示向量时,不同位置上的数字代表在相应坐标轴上的投影长度
(2)当把向量视作一种运动时,向量加法可以视为依次进行各个运动,即向量的首尾相连,反映到数值上,就是对应数值项的相加
(3)从几何角度看,向量数乘就是向量的缩放,反映到数值上,就是各个数值项都乘以标量
(4)线性代数的两种基本运算:向量加法和向量数乘
二、线性组合、张成的空间、基
(1)向量:基向量根据坐标值进行缩放并相加的结果 //用数字描述向量时,都依赖于当前采用的基
(2)线性组合(数乘和加法):两个数乘向量的和(二维) $a\vec{v}+b\vec{w}$ //缩放再相加
注:线性的一种解释——当固定其中一个标量$a$时,让另一个标量$b$自由变化时,组合向量的终点会形成一条直线
(3)向量张成的空间:给定向量所有线性组合向量的集合
(4)线性相关:存在某向量可以表示为其他向量的线性组合 $\vec{u}=a\vec{v}+b\vec{w}$,即此向量落在其他向量张成的空间中,可以移除而不减小张成的空间
(5)线性无关:所有向量都给张成的空间添加新的维度
(6)基:向量空间的一组基是张成该空间的一个线性无关向量集
三、矩阵与线性变换
(1)变换与函数类似,接收输入,生成输出,变换隐含可以用运动的思想进行理解
注:此处变换接收一个向量,并输出一个向量,可以视为将输入向量移动到输出向量
(2)线性变换的特殊之处:变换保持网格线平行且等距分布
- 所有直线在变换后仍然保持为直线,不能有所弯曲
- 原点位置必须保持固定
(3)线性变换只需要记录基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix}$ 和 $\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix}$ 变换后的位置
注:线性变换由它对空间基向量的作用完全决定
(4)重要推论:因为线性变换网格线平行且等距分布,所以变换前后向量关于基向量的线性组合保持不变!
假设原始向量为$\begin{bmatrix}x \\ y\end{bmatrix}$,当基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix}$和 $\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix}$变为$\hat{i}=\begin{bmatrix}1 \\ -2\end{bmatrix}$和 $\hat{j}=\begin{bmatrix}3 \\ 0\end{bmatrix}$时,原始向量变为:
$$\begin{bmatrix}x \\ y\end{bmatrix} \rightarrow x\begin{bmatrix}1 \\ -2\end{bmatrix}+y\begin{bmatrix}3 \\ 0\end{bmatrix}=\begin{bmatrix}1x+3y \\ -2x+0y\end{bmatrix}=\begin{bmatrix}\color{red}1 & \color{red}3\\ \color{red}-\color{red}2 & \color{red}0\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}$$
可以看出,二维线性变换仅由四个数字完全确定,而这四个数字对应于基向量变换后的坐标
因此,可以看出矩阵就是对线性变换的一种描述,其中不同列表示不同基向量变换后的结果;矩阵的乘法视为变换后基向量的线性组合 //矩阵向量乘法用于计算线性变换作用于给定向量的结果
$$\begin{bmatrix}\color{red}a & \color{blue}b\\ \color{red}c & \color{blue}d\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=x\begin{bmatrix}\color{red}a \\ \color{red}c \end{bmatrix}+y\begin{bmatrix} \color{blue}b\\ \color{blue}d\end{bmatrix}=\begin{bmatrix}{\color{red}ax }+\color{blue}by\\ {\color{red}cx}+\color{blue}dy\end{bmatrix}$$
注:矩阵代表对空间的一种特定线性变换
四、 矩阵乘法与线性变换复合
(1)矩阵乘法的几何意义:两个线性变换相继作用的合成 //独立变换的“复合变换”
(2)追踪基向量的变化:
$$\begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}\color{blue}e & \color{blue}f\\ \color{blue}g & \color{blue}h\end{bmatrix}=\begin{bmatrix}ae+bg & af+bh\\ ce+dg& cf+dh\end{bmatrix}$$
基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix} \rightarrow \begin{bmatrix}e \\ g\end{bmatrix} \rightarrow \begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}e \\ g\end{bmatrix}=\begin{bmatrix}ae+bg\\ ce+dg\end{bmatrix}$
基向量$\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix} \rightarrow \begin{bmatrix}f \\ h\end{bmatrix} \rightarrow \begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}f\\ h\end{bmatrix}=\begin{bmatrix}af+bh\\ cf+dh\end{bmatrix}$
(3)矩阵乘法不符合交换律,但满足结合律
附注1——三维空间中的线性变换:追踪三维基向量的变化 //三维方阵
五、行列式:线性变换改变面积的比例 //三维为体积的缩放
(1)含义(绝对值)
- 给定区域面积增大或减小的比例
- 空间拉伸或挤压的程度
- 单位正方形的面积变化比例
(2)矩阵行列式为0:对应变换将空间压缩到更低的维度 //列线性相关
(3)行列式的正负号:对空间定向orientation的改变,定向发生改变则为负
注:
- 可根据基向量$\hat{i}$和$\hat{j}$进行考虑,$\hat{j}$位于$\hat{i}$左侧为正,$\hat{j}$位于$\hat{i}$右侧为负
- 三维空间的定向:右手法则;如果变换后不符合右手法则,符合左手法则,则行列式为负

(4)计算行列式:$$det\left(\begin{bmatrix}a & b\\c & d\end{bmatrix}\right)=ad-bc$$ //二维方阵
六、逆矩阵、列空间与零空间
(1)求解常系数线性方程组 $A\vec{x}=\vec{v}$
$$\begin{array}{c} 2x+5y+3z=-3\\4x+0y+8z=0\\1x+3y+0z=2\\\end{array} \rightarrow \begin{bmatrix}2 & 5 & 3\\4 & 0 & 8\\ 1 & 3 & 0\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}-3\\0\\2\end{bmatrix}$$
方程$A\vec{x}=\vec{v}$的几何含义:寻找向量$\vec{x}$,使得其经过变换$A$后得到向量$\vec{v}$
(2)行列式$det(A)\neq 0$时 //唯一解
有且仅有一个向量满足该变换$\vec{x}=A^{-1}\vec{v}$
此时存在逆变换$A^{-1}$,满足$A^{-1}A=I$(恒等变换)
(3)行列式$det(A)=0$时
- 有解的条件:向量$\vec{v}$位于变换后的低维空间内 //列空间
(4)列空间:变换后的基向量(矩阵的列)所能张成的空间 $A\vec{x}$ //解决“何时存在解”
- 一定包含零向量
(5)秩rank:变换后的空间的维数 //列空间的维数
- 满秩full rank:秩与列数相等;列空间的维数与输入空间的维数相等
- 对于满秩矩阵而言,只有零向量在变换后仍落在原点处
- 对于非满秩矩阵,存在多个向量变换后落在原点
(6)矩阵的零空间(核kernel):变换后落在原点的向量$\vec{x}$集合,即满足$A\vec{x}=\vec{0}$ //解决“解是什么样的”
附注2——非方阵
(1)$m\times n$矩阵:将$n$维向量变换为$m$维向量 //$m\neq n$时,基向量的维度发生变化
(2)矩阵的列数表明基向量的个数(输入空间的维数),矩阵的行数表明变换后输出空间的维数
七、点积与对偶性 //点积:高维输入,一维输出
(1)$\vec{v}\cdot\vec{w}$标准定义:同维向量对应坐标项相乘后,求和
(2)$\vec{v}\cdot\vec{w}$几何解释:$\vec{v}$在$\vec{w}$方向上的投影长度和$\vec{w}$长度的乘积 //同向为正,反向为负,垂直为0
注:投影的对称性——点积的结果与顺序无关 $\vec{v}\vec{w}=\vec{w}\vec{v}$

(3)实现“高维输入,一维输出”的线性变换需要满足的直观条件:一系列等距分布于一条直线上的点,应用线性变换后,会保持这些点的等距分布特性;若干输出不是等距分布,则变换不是线性的
注:一维行向量可以视为高维空间向一维空间的变换矩阵,每个元素可以看作基向量的变换结果,如$\begin{bmatrix}2 & 1\end{bmatrix}$
- 点积与变换的关联:

- 向量与变换之间的关系(直立和放倒)
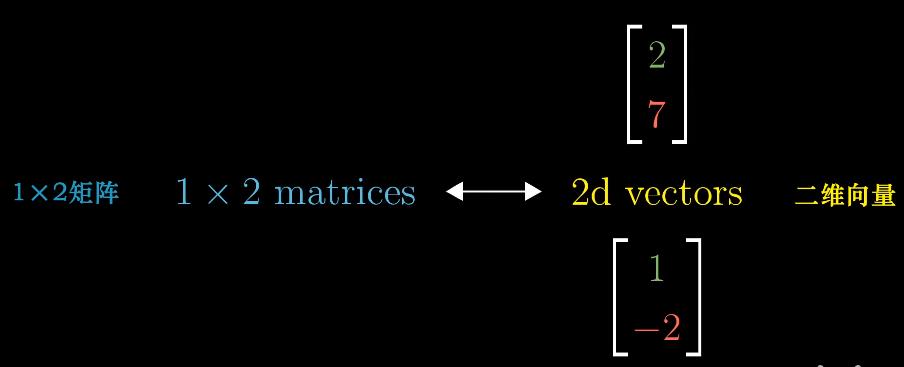
- 投影矩阵projection matrix:二维向量到数的线性变换 //空间任意向量经过投影变换的结果为投影矩阵与向量相乘
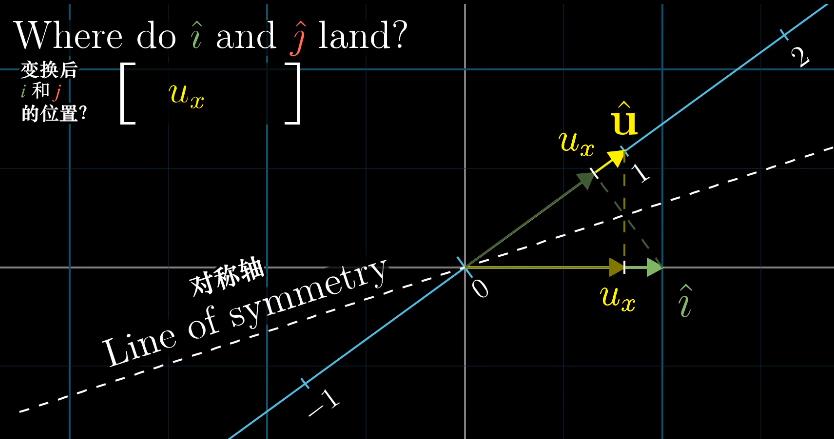
如图所示,$\hat{i}$和$\hat{j}$在单位向量$\hat{u}$上的投影值,分别为$u_x$和$u_y$(投影变换矩阵的值);则投影变换与点积的关系如下:
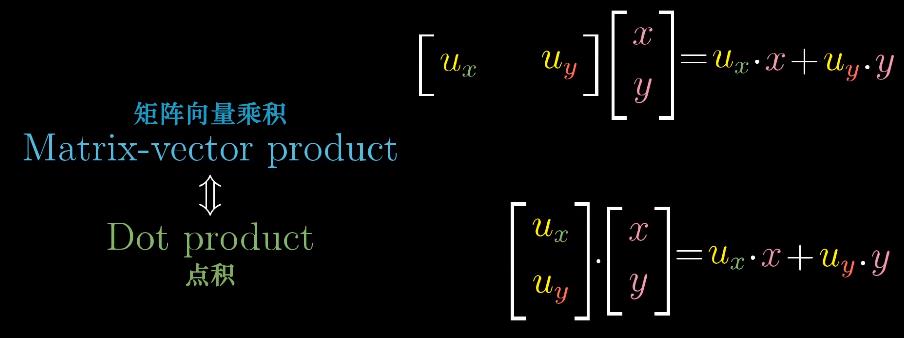
注:任何时候看到一个输出空间为一维数轴的线性变换,空间中会存在唯一的向量$v$与之相关,所以应用变换和与向量$v$做点积是一样的(对偶性duality)

- 向量 $\Leftrightarrow$ 对应的线性变换 //向量是线性变换的物质载体
- 多维空间到一维空间的线性变换 $\Leftrightarrow$ 多维空间的某个特定向量 //应用线性变换和与这个向量点乘等价
总结:
- 点积是理解投影的有利几何工具,并便于检验两个向量的指向是否相同
- 两个向量点乘:将其中一个向量转换为线性变换
八、叉积
1. 标准介绍
(1)二维叉积(等价于行列式):
$\overrightarrow{v}\times\overrightarrow{w}$ = 构成的平行四边形的面积 * 方向($\overrightarrow{v}$在$\overrightarrow{w}$右侧为正,否则为负) //乘积顺序有影响
注:
- 判断方向的方法,记住横轴单位向量$\hat{i}$与纵轴单位向量$\hat{j}$的叉积$\hat{i}\times\hat{j}$为正 //基向量的顺序就是定向的基础
- 面积的求法:将向量作为列构成矩阵(与将$\hat{i}$和$\hat{j}$分别移至$\overrightarrow{v}$和$\overrightarrow{w}$的线性变换相对应),矩阵行列式的绝对值即为面积 //作为行也可以,因为转置不改变行列式的值

(2)三维叉积:通过两个三维向量生成一个新的三维向量 $\overrightarrow{v}\times\overrightarrow{w}=\overrightarrow{p}$

- 生成的三维向量:长度为平行四边形的面积,方向垂直于平行四边形,且符合右手法则

2. 以线性变换的眼光看叉积
(1)线性变换和对偶向量

(2)理解叉积的计算公式和几何含义之间的关系

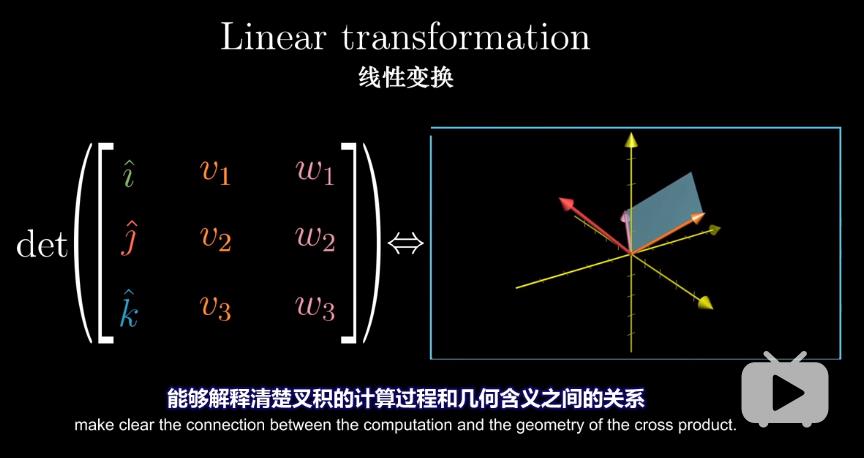
- 定义三维空间到数轴的函数:输入任意向量$(x, y, z)$计算与$\overrightarrow{v}$和$\overrightarrow{w}$确定的平行六面体的体积(考虑方向)

注:根据行列式的性质可以证明该函数是线性的
- 寻找对偶向量$\overrightarrow{p}$:线性变换$\Rightarrow$矩阵乘法$\Rightarrow$向量点积
注:寻找向量$\overrightarrow{p}$,满足与向量$(x,y,z)$点乘时,所得结果为右侧$3\times 3$矩阵的行列式
 $$\Downarrow$$
$$\Downarrow$$

注:计算公式角度
- 向量$\overrightarrow{p}$点积的几何意义:

- 六边体体积计算两种思考方式:
- 线性函数对于给定向量的作用为:将向量投影到垂直于$\overrightarrow{v}$和$\overrightarrow{w}$的直线上,然后将投影长度与$\overrightarrow{v}$和$\overrightarrow{w}$张成的平行四边形的面积相乘 //对行列式的解释
- 等价于:垂直于$\overrightarrow{v}$和$\overrightarrow{w}$且长度为平行四边形面积的向量与向量$(x,y,z)$进行点乘 //对对偶向量点乘的解释
注:几何意义角度
九、基变换
(1)不同基向量(坐标系)下的坐标表示
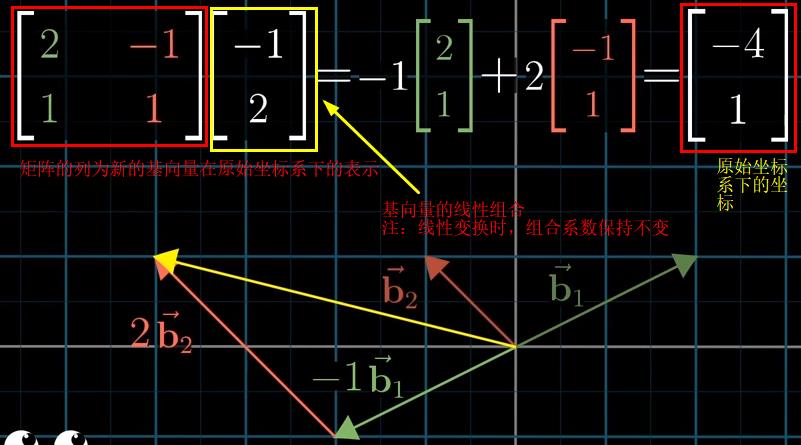
注:当坐标均为$\begin{bmatrix}-1 \\ 2\end{bmatrix}$时,基向量的不同会引起在同一坐标系进行表示时的坐标变化
(2)基变换:矩阵代表基向量的变换
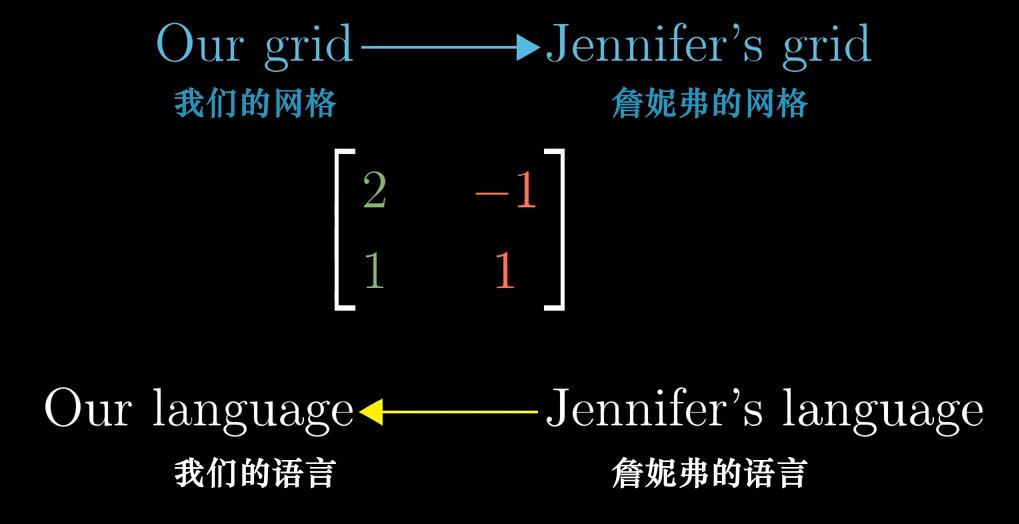


(3)基变换图示
- 基变换矩阵(描述基变量的变化)

- 正变换

- 逆变换

(4)如何利用标准坐标系描述新基下的线性变换

注:先将新基下的向量转化为标准坐标系表示——>在标准坐标系下进行变换——>将坐标重新变换回新基下的坐标

注:表达式$\color{red}{A^{-1}MA}$暗示了一种数学上的转移作用,中间的矩阵$M$代表了一种标准坐标系下的常见变换,外侧的两个矩阵则代表着不同坐标系的视角转化(转移作用),相应的矩阵乘积结果仍然代表着同一个变换,但是从其他人(新坐标系)的角度来看的
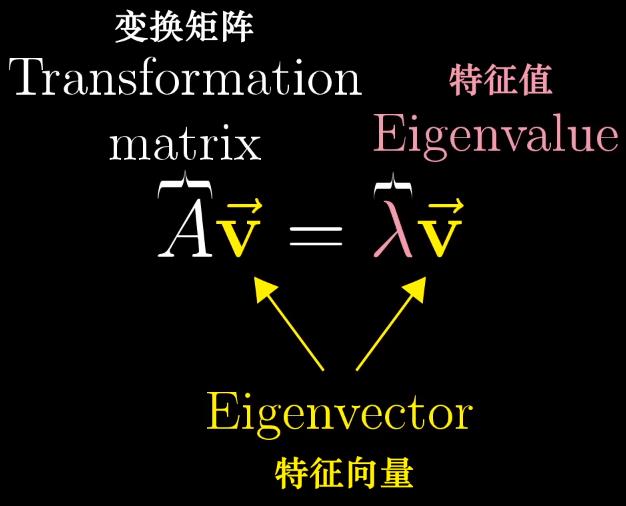
十、特征向量与特征值
(1)特征向量:矩阵变换对它的作用仅仅是拉伸或者压缩,如同一个标量 //特征向量留在自身张成的空间里(留在直线上,不发生旋转)
(2)特征值:衡量特征向量在变换中拉伸或者压缩比例的因子
(3)对于三维旋转而言,旋转矩阵的特征向量代表了该旋转的旋转轴(不发生变化) //旋转矩阵的特征值为1(保持向量长度不变)
(4)理解线性变换作用的两种方式
- 将矩阵列视为变换后的基向量 //依赖于所选特定坐标系
- 利用特征向量和特征值 //不依赖于坐标系
(5)求解特征向量、特征值


注:当且仅当矩阵$A-\lambda I$代表的变换将空间压缩到更低的维度时,才会存在非零向量$\vec{v}$,使得和矩阵的乘积为零,也就是矩阵的行列式需要为零
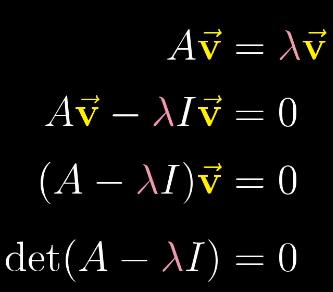
(6)二维线性变换不一定有特征向量:如逆时针旋转90度$\begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix}$使得每个向量都发生旋转(离开其张成的空间),此时求解行列式为零得不到实数解,表明没有特征向量
注:与虚数$i$相乘在复平面中表现为90度旋转(与$i$是上述旋转变换的特征值有关联);特征值出现复数的情况一般对应于变换中的某种旋转
(7)剪切变换矩阵$\begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix}$的所有特征向量都位于$x$轴上,特征值为1
注:可能出现只有一个特征值,但是特征向量不止在一条直线上,如$\begin{bmatrix}2 & 0 \\ 0 & 2\end{bmatrix}$的唯一特征值为2,但是平面内每个向量都是特征向量
(8)特征基eigenbasis:一组特征向量作为基向量构成的集合
- 对角矩阵的所有基向量都是特征向量,矩阵的对角元为相应的特征值 //对角矩阵仅仅让基向量与某个特征值相乘

- 当基向量不是特征向量时,可以通过基变换,将坐标系转换为由特征向量作为基向量(特征向量足够多,能够张成全空间)
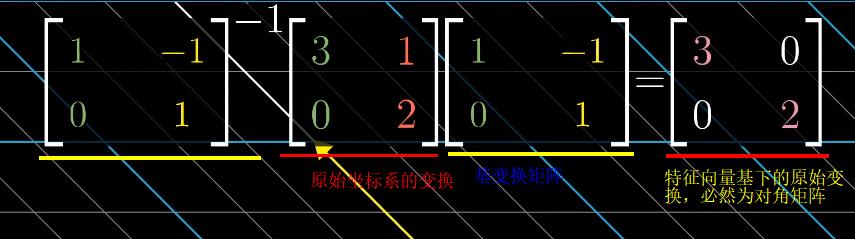
注:同一个变换在新基(特征向量)$\begin{bmatrix}1 & 0 \\ -1 & 1\end{bmatrix}$下表示为对角矩阵,且对角线元素为特征值
十一、抽象向量空间 //类似向量的事物合集,如箭头、一组数、函数等
(1)向量——>函数
- 可加性

- 成比例性

注:可加性和成比例性的直观解释——网格线保持平行且等距分布
- 线性变换(矩阵)和线性算子(求导)之间的对应关系

- 向量空间必须满足的八条公理:

(2)全体多项式空间的基函数basis functions为:$b_0(x)=1, b_1(x)=x, b_2(x)=x^2, b_3(x)=x^3, \cdots$;
对每个基函数求导,并将结果作为矩阵列,可得函数的求导变换矩阵$\frac{d}{dx}$

(3)普适的代价




