麻省理工公开课：线性代数 第7课 求解Ax=0：主变量、特解

参考资料：

网易公开课：http://open.163.com/special/opencourse/daishu.html　　麻省理工公开课：线性代数

教材：Introduction to Linear Algebra, 4th edition  by Gilbert Strang

链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg 
提取码：s9bl 

假设：$A$为$3\times 4$长方形矩阵（线性相关），求解$A\mathbf{x}=0$

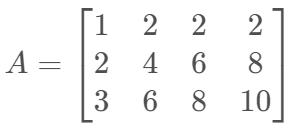
一、消元elimination（不改变零空间$N(A)$）：得到行阶梯形式(row echelon form)的$U$

（1）消元的过程中，方程组的解$\mathbf{x}$不变，因此零空间不变，但是会改变列空间。

（2）可以看出主元的数量为2，即矩阵的秩为2　　//rank of $A$ = 主元(pivot)个数

（3）主元对应的列为“主列”(1、3)，其他列被称为“自由列”(2、4)　　//自由列的含义对应变量（本例为$x_2, x_4$）为可以取任意值，通过回代求得主列（本例为$x_1, x_3$）的值

（4）分别令自由变量$(x_2, x_4)$为(1,0)和（0,1），回代入方程组$U\mathbf{x}=0$求得$x_1, x_3$（两组特解），最终构造包含所有解的零空间$N(A)$为：

注：

• 零空间为特解的线性组合，特解的个数与自由变量的个数一致　　//若$m\times n$矩阵的秩为$r$，则自由变量的个数为$n-r$
• 无自由变量时，零空间仅包含零向量

（5）求解$A\mathbf{x}=0$步骤：消元 —> 确定主元个数 —> 设置自由变量取值，利用回代法求解特解 —> 根据特解构造零空间

（6）简化的行阶梯形式(reduced) $R$：令主元为1，且主元上下均为0　　//$R\mathbf{x}=0$

注：全0行表示原来的行是其他行的线性组合，所以被消元步骤消去

（7）将主列和自由列分别放在一起，可以得到：

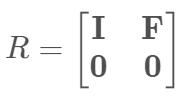
　　求解$R\mathbf{x}=0$可以直接求解$RN=0$：

 

注：零空间矩阵$N$的各列为求得的各个特解