麻省理工公开课：线性代数 第6课 列空间和零空间

参考资料：

网易公开课：http://open.163.com/special/opencourse/daishu.html　　麻省理工公开课：线性代数

教材：Introduction to Linear Algebra, 4th edition  by Gilbert Strang

链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg 
提取码：s9bl 

一、向量空间和子空间（加法封闭、数乘封闭）

向量空间$R^3$的子空间：$R^3$、任意经过原点$(0, 0, 0)$的平面$P$和直线$L$、只包含零向量的空间$Z$

并集：$P\bigcup L$是子空间吗？　　//否！对加法运算不封闭

交集：$P\bigcap L$是子空间吗？　　//是！

结论：任意子空间的交集仍然是子空间

二、矩阵列空间 $C(A)$：所有列向量的线性组合构成的子空间

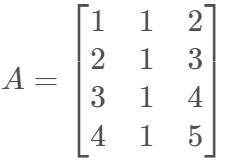
（1）因为$A$为$4\times 3$矩阵，列向量为四维向量，所以列空间$C(A)$是$R^4$的子空间（真子空间）

（2）$A\mathbf{x}=\mathbf{b}$对任何$\mathbf{b}$都有解吗？　　//否！当且仅当$\mathbf{b}$位于矩阵$A$的列空间$C(A)$时，有解！

（3）由于矩阵$A$的第三列为前两列的线性组合（和），所以列向量是线性相关的，列空间$C(A)$仅为$R^4$的二维子空间

三、矩阵零空间 $N(A)$：$A\mathbf{x}=\color{red}0$的所有解$\mathbf{x}$构成的子空间　　//与$\mathbf{b}$无关，等价于$\mathbf{b}=\mathbf{0}$

（1）因为$A$为$4\times 3$矩阵，向量$\mathbf{x}$为三维向量，所以零空间$N(A)$是$R^3$的子空间

（2）本例的零空间为$R^3$中的一条直线$c(1, 1, -1)$　　//记(1, 1, -1)为列向量，[1 1 -1]为行向量

（3）验证 $N(A)$为子空间

　　假设：$A\mathbf{v}=0$、$A\mathbf{w}=0$

　　则：$A(\mathbf{v}+\mathbf{w})=A\mathbf{v}+A\mathbf{w}=0$（加法封闭）

　　　　$A(c\mathbf{v})=cA\mathbf{v}=0$（数乘封闭）

（4）$A\mathbf{x}=\mathbf{b}, \mathbf{b}\neq\mathbf{0}$ 的所有解是否构成子空间？　　//否！解中不包含原点$\mathbf{0}$，本例中所有的解构成不穿过原点的直线

四、构造子空间的两类方法

（1）已知空间内的向量，通过线性组合进行构造　　//列空间

（2）已知空间内向量必须满足的方程组，而空间内的向量未知　　//零空间