麻省理工公开课：线性代数 第4课 A的LU分解

参考资料：

网易公开课：http://open.163.com/special/opencourse/daishu.html　　麻省理工公开课：线性代数

教材：Introduction to Linear Algebra, 4th edition  by Gilbert Strang

链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg 
提取码：s9bl 

一、$A=LU$

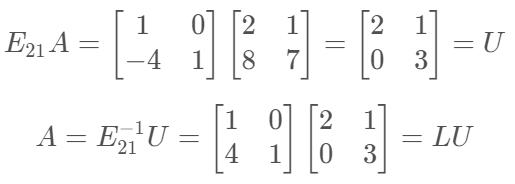
其中，$L$为下三角矩阵，$U$为上三角矩阵；将主元提取出来可得：

其中，$D$为包含主元的对角矩阵

三维矩阵情形（无行交换）：

$$EA=E_{32}E_{31}E_{21}A=U \Rightarrow A=\color{red}{E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}}U=LU$$

二、置换矩阵$P$（行或列交换）：行重新排列的单位矩阵

（1）性质：$P^{-1}=P^{T}$　　//矩阵的转置和逆相等，即$\color{red}{P^TP=I}$

（2）三维情形有6种置换矩阵：

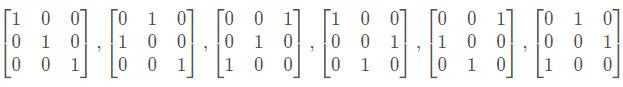
（3）四维矩阵有24种置换矩阵

 

注：$n\times n$矩阵的置换矩阵个数为$n!$（n的阶乘）