线性代数导论（一）向量介绍

参考资料：《Introduction to linear algebra》4th edition by Gilbert Strang

链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg 
提取码：s9bl 

网易公开课：http://open.163.com/special/opencourse/daishu.html　　麻省理工公开课：线性代数

思考：

（一）相似矩阵是同一个线性变换的不同描述矩阵

（二）对象的变换等价于坐标系的变换（运动是相对的），如对于变换$Ma=b$，可以看作$Ma=Ib$，坐标系$M$和$I$类似于环境声明，$a$和$b$为相应坐标系下的坐标向量；求解上述变换可得$Ia=IM^{-1}b$，当坐标系声明均为$I$时，可得$a=M^{-1}b$

 

1. 线性组合：向量加法和标量乘法的组合

其中，$c,d$为标量，$\mathcal{v},\mathcal{w}$为向量

2. 向量点积/内积：对应元素相乘后相加

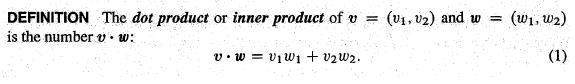
（1）点积为0，则表示两个向量相互垂直（$\cos\theta=0$，夹角为90度）

（2）向量的长度：向量与自身点积的平方根

（3）单位向量的长度为1，可以通过非零向量与自身长度相除得到

（4）两个单位向量的点积即为夹角的余弦值（夹角小于90度为正，夹角大于90度为负）

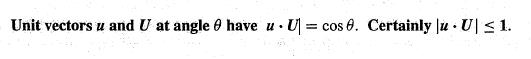
例如，当$\mathcal{u}$为单位旋转向量$(\cos\theta, \sin\theta)$，$\mathcal{i}$为单位向量$(1,0)$时，$u\cdot i=\cos\theta$；同时旋转$\alpha$，即$\beta=\theta+\alpha$，点积为$\cos\alpha\cos\beta+\sin\alpha\sin\beta=\cos(\beta-\alpha)=\cos\theta$

（5）当向量不是单位向量时，相应的余弦定理如下：

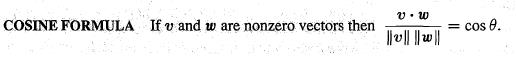
由于$|\cos\theta|\leq 1$，可以得到施瓦茨不等式（内积的绝对值不超过长度的乘积）和三角不等式（两边之和大于第三边）如下：

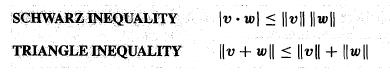
注：三角不等式的证明如下

$$\parallel\mathcal{v}+\mathcal{w}\parallel^{2} = \parallel\mathcal{v}\parallel^{2} + 2\mathcal{v}\mathcal{w} + \parallel\mathcal{w}\parallel^{2} \leq \parallel\mathcal{v}\parallel^{2} + 2\parallel\mathcal{v}\parallel\parallel\mathcal{w}\parallel + \parallel\mathcal{w}\parallel^{2} =  (\parallel\mathcal{v}\parallel + \parallel\mathcal{w}\parallel)^{2}$$

当$\mathcal{v}=(a,b)$，$\mathcal{w}=(b,a)$时，施瓦茨不等式为：$2ab\leq a^2+b^2$；令$x=a^2, y=b^2$，可以得到几何均值$\sqrt{xy}$小于算数均值$\frac{1}{2}(x+y)$的结论：

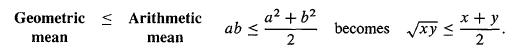
 3. 矩阵和向量的乘积可以看作是矩阵各列的线性组合

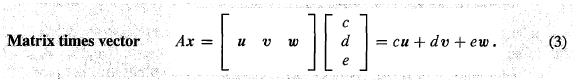
4. 向量线性无关和线性相关

线性相关的$n*n$方阵不可逆