Python学习(六)向量化
参考资料:
https://github.com/lijin-THU/notes-python(相应实体书为:《自学Python——编程基础、科学计算及数据分析》)
1. 向量化函数
(1)自定义sinc函数
1 import numpy as np 2 3 def sinc(x): 4 if x == 0.0: 5 return 1.0 6 else: 7 w = np.pi * x 8 return np.sin(w) / w
可以作用于单个数值:如sinc(0)、sinc(3.0);但是不能作用于数组x = np.array([1,2,3]);sinc(x) 报错
(2)可以使用 numpy 的 vectorize 将函数 sinc 向量化,产生一个新的函数
1 x = np.array([1,2,3]) 2 vsinc = np.vectorize(sinc) 3 vsinc(x) #作用是为x中的每一个值调用sinc函数
1 import matplotlib.pyplot as plt 2 %matplotlib inline 3 4 x = np.linspace(-5,5,101) 5 plt.plot(x, vsinc(x))
注:因为这样的用法涉及大量的函数调用,因此,向量化函数的效率并不高
2. 二元运算
(1)四则运算

1 import numpy as np 2 a = np.array([1,2]) 3 a * 3 #数组与标量相乘,相当于数组的每个元素乘以这个标量 4 5 a = np.array([1,2]) 6 b = np.array([3,4]) 7 a * b #数组相乘,结果为逐个元素对应相乘 8 np.multiply(a, b) #使用函数 9 np.multiply(a, b, a) #如果有第三个参数,表示将结果存入第三个参数中
(2)比较和逻辑运算 //大部分逻辑操作是逐个元素运算的,返回布尔数组
1 a = np.array([[1,2,3,4], 2 [2,3,4,5]]) 3 b = np.array([[1,2,5,4], 4 [1,3,4,5]]) 5 a == b #等于操作是对应元素逐个进行比较的,返回的是等长的布尔数组
注:如果在条件中要判断两个数组是否一样时,不能直接使用 if a==b: 需要使用 if all(a==b):
对于浮点数,由于存在精度问题,使用函数 allclose 会更好 if allclose(a,b):
3. ufunc对象
(1)Numpy有两种基本对象:ndarray (N-dimensional array object) 和 ufunc (universal function object);ndarray 是存储单一数据类型的多维数组,而 ufunc 则是能够对数组进行处理的函数。例如,我们之前所接触到的二元操作符对应的 Numpy 函数,如 add,就是一种 ufunc 对象,它可以作用于数组的每个元素。
1 import numpy as np 2 a = np.array([0,1,2]) 3 b = np.array([2,3,4]) 4 np.add(a, b) #作用于每个元素,逐个元素相加,输出array([2, 4, 6])
注:大部分能够作用于数组的数学函数如三角函数等,都是 ufunc 对象
(2)可以查看ufunc对象支持的方法,如np.add对象:dir(np.add)
- reduce方法:op.reduce(a) 将操作opp沿着某个轴应用,使得数组
a的维数降低一维;
1 a = np.array([1,2,3,4]) 2 np.add.reduce(a) #add 作用到一维数组上相当于求和(降低一维);输出10
1 a = np.array([[1,2,3],[4,5,6]]) 2 np.add.reduce(a) #多维数组默认只按照第一维进行运算;输出array([5, 7, 9])
3 np.add.reduce(a, 1) #指定维度,输出array([ 6, 15])
1 a = np.array(['ab', 'cd', 'ef'], np.object) 2 np.add.reduce(a) #作用于字符串,输出'abcdef' 3 4 a = np.array([1,1,0,1]) 5 np.logical_and.reduce(a) #逻辑与,输出False 6 np.logical_or.reduce(a) #逻辑或,输出True
- accumulate方法op.accumulate(a):保存reduce方法每一步结果所形成的数组
1 a = np.array([1,2,3,4]) 2 np.add.accumulate(a) #array([1,3,6,10],dtype=int32) 3 4 a = np.array(['ab', 'cd', 'ef'], np.object) 5 np.add.accumulate(a) #array(['ab','abcd','abcdef'],dtype=object) 6 7 a = np.array([1,1,0,1]) 8 np.logical_and.accumulate(a) #array([True, True, False, False]) 9 np.logical_or.accumulate(a) #array([True, True, True, True])
- reduceat方法op.recuceat(a, indices):将操作符运用到指定的下标上,返回一个与indices大小相同的数组
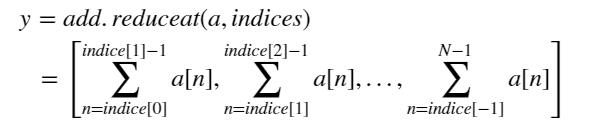
1 a = np.array([0, 10, 20, 30, 40, 50]) 2 indices = np.array([1,4]) 3 np.add.reduceat(a, indices) #输出array([60, 90])
#60为从下标1(包括)到下标4(不包括)的运算结果;90位下标4(包括)到结尾的操作结果
- outer方法op.outer(a,b):对于
a中每个元素,将op运用到它和b的每一个元素上所得到的结果(结果大小为a.size*b.size)
1 a = np.array([0,1]) 2 b = np.array([1,2,3]) 3 #操作顺序有区别 4 np.add.outer(a, b) #array([[1,2,3],[2,3,4]]) 5 np.add.outer(b, a) #array([[1,2],[2,3],[3,4]])
4. choose函数实现条件筛选(类似switch和case操作)
1 import numpy as np 2 control = np.array([[1,0,1], 3 [2,1,0], 4 [1,2,2]]) 5 #control控制元素的对应下标,将下标0、1、2的值分别映射为10,11,12 6 np.choose(control, [10, 11, 12])
#结果和control大小相同,为
array([[11, 10, 11], [12, 11, 10], [11, 12, 12]])
1 i0 = np.array([[0,1,2], 2 [3,4,5], 3 [6,7,8]]) 4 i2 = np.array([[20,21,22], 5 [23,24,25], 6 [26,27,28]]) 7 control = np.array([[1,0,1], 8 [2,1,0], 9 [1,2,2]]) 10 #根据choose中对应下标所在位置,映射为下标对应的数组的相应位置 11 np.choose(control, [i0, 10, i2]) #0对应i0,1对应10,2对应i2
输出:array([[10, 1, 10], [23, 10, 5], [10, 27, 28]])
#将数组中所有小于10的值变为10
1 a = np.array([[ 0, 1, 2], 2 [10,11,12], 3 [20,21,22]]) 4 np.choose(a < 10, (a, 10)) #True=1对应于10,False=0对应于数组a(选取相应位置的值)
1 a = np.array([[ 0, 1, 2], 2 [10,11,12], 3 [20,21,22]]) 4 5 lt = a < 10 6 gt = a > 15 7 #将数组中所有小于 10 的值变成了 10,大于 15 的值变成了 15 8 choice = lt + 2 * gt #0对应a,1对应10,2对应15 9 np.choose(choice, (a, 10, 15))
5. 数组广播机制
1 import numpy as np 2 a = np.array([[ 0, 0, 0], 3 [10,10,10], 4 [20,20,20], 5 [30,30,30]]) 6 b = np.array([[ 0, 1, 2], 7 [ 0, 1, 2], 8 [ 0, 1, 2], 9 [ 0, 1, 2]]) 10 a + b #正常加法 11 12 b = np.array([0,1,2]) #b为一维数组array([0,1,2]),shape为(3,) 13 a + b #将b扩展为先前的数组形状 14 15 a = np.array([0,10,20,30]) #此时a.shape为(4,),a+b会由于维度不匹配报错
ValueError: operands could not be broadcast together with shapes (4,) (3,)
16 a.shape = 4,1 #等价于a= a[:, np.newaxis],a为一维列向量array([[0],[10],[20],[30]]),shape为(4,1) 17 a+b #二者均自动扩展为最初数组形状
对于 Numpy 来说,维度匹配当且仅当:
- 维度相同
- 有一个的维度是1
匹配会从最后一维开始进行,直到某一个的维度全部匹配为止

1 x = np.linspace(-.5,.5, 21) #(21,) 2 y = x[:, np.newaxis] #(21,1) 3 radius = np.sqrt(x ** 2 + y ** 2) #因为y存在一维,所以自动扩展x、y为21*21 4 import matplotlib.pyplot as plt 5 %matplotlib inline 6 7 plt.imshow(radius)



