10.30 CF1685 题解

10.30 CF1685

A.Circular Local MiniMax

题意

给你 \(n\) 个整数 $ a_1, a_2, \ldots, a_n $ 。 问有没有可能将它们排列在一个圆上，使每个数字严格地大于其相邻的两个数字或严格地小于其相邻的两个数字？

题解

直接排序然后按照 \(1,4,2,5,3,6\) 的规律放，check 一下合不合法就行了。

B.Linguistics

题意

给你一个 AB 串 \(s\)，问你是否可以用 \(a\) 个 A，\(b\) 个 B，\(c\) 个 AB，\(d\) 个 BA 拼接成 s。

题解

首先我们把连续的 \(AB\) 交替出现的串分离出来。

例如样例 BBABABABABBBABABABABABABAABABA，

我们分离成 B[BABABABAB]B[BABABABABABABA][ABABA]

我们发现分离之后单个的 A/B 只能用单个的填，我们就只用考虑连续交替串。

我们把连续交替串按照长度奇偶分为两类：

• 长度为奇数，开头结尾重复了一个一样的，例如 [ABABA] 我们填它的方法是用 1 个开头结尾出现的单个字符 A 和 \(\frac {len-1} 2\) 个 AB/BA。

• 长度为偶数，例如 [BABABABABABABA]，就有两种情况：

  • 1.用 \(\frac {len} 2\) 个 BA 填充。

  • 2.用 \(\frac{len}2 - 1\) 个 AB/BA 填充，用 1 个 A 和 1 个 B 填充。

因为 1 个 A 和 1 个 B 可以拼成一个 AB/BA ，所以我们尽量要先消耗 AB/BA ，保留 A/B。

长度为奇数的填充方法是唯一的，我们先贪心考虑长度为偶数的。

先按长度从小到大排序，能用方法 1 填的尽量用方法 1，这样消耗的单个 A/B 是最少的。

剩下的记录 AB/BA 都可以选的然后判断 \(ab + ba\) 和它大小相等不相等。

注意 1 个 A 和 1 个 B 可以拼成一个 AB/BA。

C. Bring Balance

题意

给你一个括号序列，你可以翻转任意子串，问最少几次反转成合法括号序列。

翻转指 ABC->CBA。

题解

看到括号序列就先想把折线图画出来。

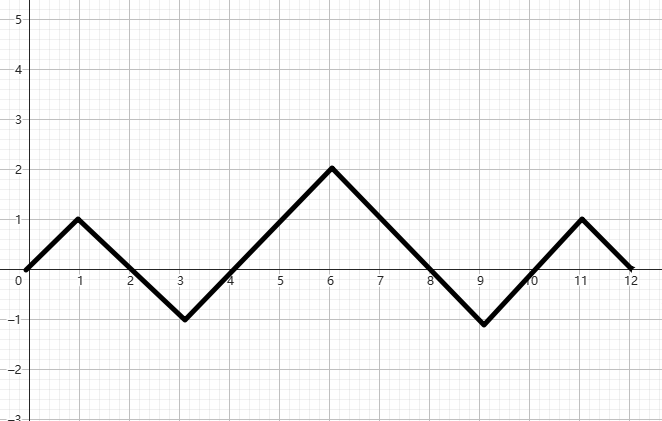
样例 ())((()))(()。

把 ( 看做 \(+1\)，) 看做 \(-1\)，点坐标就是前缀和。

我们发现操作区间 \([l,r]\) 等同在折线图上把区间 \([l,r]\) 里面的图形按照 \(l\) 点和 \(r\) 点的中点进行中心对称。

我们发现找出全局最高的点 \(w\)，将 \([1,w]\) 和 \([w + 1, n]\) 操作一定会使括号序列合法，所以最多操作两次。

接下来考虑只操作一个区间 \([l,r]\) 的情况。

首先在 \(y=0\) 以下的点必须被翻转到，我们找到左边第一个在 \(y=0\) 以下的点，\(l\) 一定在这个区间内找，\(r\) 同理。

在区间内找一个最高的点，这样 \(l,r\) 的中点尽可能高，本身在上面的点更不容易翻下去。

然后 check 一下合不合法。

注意特判不需要操作的情况。