9.11 CF1819 题解
9.11CF1819 题解
A. Constructive Problem
简单题，上链接：
B. The Butcher
题意
有一张 \(h \times w\) 的纸片，现在对这张纸片进行 \(n−1\) 次裁剪。每次裁剪后会将其中一半收归（即这一半不会再被裁剪）。
保证纸片不会被旋转。
告诉你最终裁剪后的 \(n\) 张纸片长宽，问初始有多少 \(h\times w\) 的纸片可以裁剪成这 \(n\) 张纸片，输出所有可行解。
题解
考虑第一次剪的那一刀一定会保留下来一个 \(h\) 或者 \(w\)。
\(h_i\) 和 \(w_i\) 分别求最大，然后有可能 \(h = h_{max}\) 或者 \(w = w_{max}\)。
用面积先判断一次可不可以除尽。
之后 check 再模拟把一块块拼回去，看看有没有不合法的。
check 总的来说就是反复取 \(w,h\) 最大的，然后减去这一块，若发现取出来的和当前 \(w\) 或 \(w\) 不相等，那么无解。
用 set 维护即可。
check 部分手模一下应该就知道怎么搞。
C. The Fox and the Complete Tree Traversal
题意
给定整数 \(n\) 和一棵包含 \(n\) 个节点的树。 记 \(\operatorname{Dist}(x, y)\) 表示树上节点 \(x, y\) 之间最短路径的边数。 你需要判断是否存在一个 \(1 \sim n\) 的排列 \(p\) ，满足:
- \(\operatorname{Dist}\left(p_{i}, p_{i+1}\right) \leq 2\) 对任意整数 \(i(1 \leq i<n)\) 成立。
- \(\operatorname{Dist}\left(p_{1}, p_{n}\right) \leq 2\) 。
存在则输出Yes然后输出任意一个满足要求的 \(p\) ，不存在则输出No。
例如下面的图，顺着黑色带箭头线填入排列就是一个合法解。
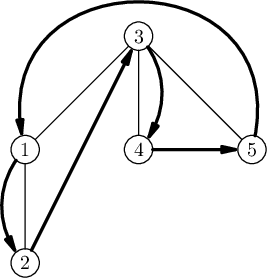
题解
不知道是怎么想出毛毛虫的，好厉害。
我们把一棵树旋转成一棵毛毛虫。
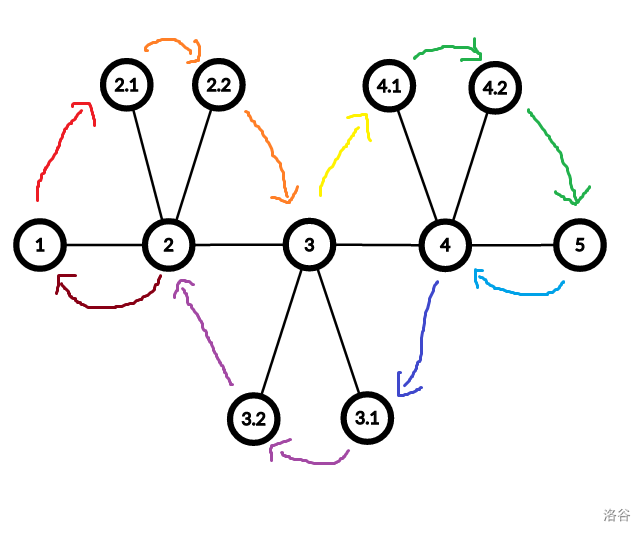
我们发现如果这个毛毛虫有长度 \(\ge2\) 的支链就无解（具体可以自己手玩尝试一下）。
然后就可以做了。
D. Misha and Apples
题意
给定 \(n\) 个集合 \(S_i\)，第 \(i\) 个集合的大小为 \(k_i\)，集合元素为 \(1\sim m\) 的正整数。特别地，若 \(k_i = 0\)，则 \(S_i\) 可以是正整数 \(1\sim m\) 的任意可空子集，由你确定。
设 可重集 \(S\)，初始为空。按编号从小到大依次遍历每个集合，往 \(S\) 中加入 \(S_i\) 所有元素。每次加入当前集合的所有元素后，若 \(S\) 包含重复元素，则清空 \(S\)。注意，一个集合内的元素 同时 被加入 \(S\)。
你需要确定 \(k_i = 0\) 的 \(S_i\) 具体包含哪些数，使得最终的 \(|S|\) 最大。求出这个最大值。
多组数据。
\(1\leq T, \sum n, m\leq 2\times 10 ^ 5\)，\(0\leq \sum k_i\leq 2\times 10 ^ 5\)，\(S_i\) 的元素互不相同。
注意不保证 \(\sum m\) 的数量级。
题解
我们考虑最晚一次清空尽量早，这样清空之后的的处理就很简单了。
我们定义 \(cl_i\) 表示枚举到当前的 \(i\) 最晚一次清空尽量早，在 \(cl_i\) 处。
我们定义 \(f_i\) 表示在 \(i\) 时候是否可以被清空。
我们定义 \(mx\) 表示 \(S_i\) 所有元素上一次出现位置最晚一次在哪里。
当前在 \(i\)，先来求 \(f_i\)：
-
如果 \(cl_{i} < mx\) ，显然当前一定出现重复元素，\(f_i = 1\)。
-
如果 \(cl_i \ge mx\)，并且 \([cl_i+1, mx]\) 之前存在一个空集，那么这个空集一定可以为我所用，让我在 \(i\) 清空，\(f_i = 1\)。
-
否则 \(f_i = 0\)。
注意我们的 \(f_i\) 表示能否被清空，而不是一定被清空。
然后来更新 \(cl_{i + 1}\) ：
初始化 \(cl_{i+1} = cl_i\)
-
如果 \(cl_{i + 1} < mx\)，那么在 \(i\) 处会被清空，我们要让最晚一次清空尽量早，我们就要让 \(mx\) 被清空掉，所以
++cl[i + 1]，直到 \(cl_{i+1} \ge mx\)，进入下面的流程。 -
如果 \(cl_{i+1} \ge mx\) ，如果 \(f_{cl_{i+1}} = 0\)，那么
++cl[i + 1]，直到 \(f_{cl_{i+1}} = 1\)
最后 \(cl_n\) 就是最晚一次清空位置了。
之后看 \(cl_n\sim n\) 有没有空集，若有答案就是 \(m\)，若没有答案就是 \(cl_n \sim n\) 集合元素个数。
