9.6 CF1830 题解

9.6 CF1830 题解

A. Copil Copac Draws Trees

链接

真弱智题不用讲

B. The BOSS Can Count Pairs

题意

每组数据给你一个 \(n\) 和两个序列 \(a,b\)。

求有多少个数对 \((i,j)\) 满足 \(1 \le i < j \le n\) 且 \(a_i \times a_j = b_i + b_j\)。

题解

考虑 \(a_i\times a_j = b_i + b_j\)，那么 \(a_i \times a_j \le 2n \to min(a_i, a_j) \le \sqrt {2n}\)。

枚举 \(x\) 表示两个a中小的那个，从 \(1 \to \sqrt {2n}\) 。

把所有满足 \(a_i = x\) 的 \(b_i\) 放在桶里，然后在桶里找 \(a_i \times x - b_i\) 个数。

复杂度 \(O(n\sqrt n)\)

C. Hyperregular Bracket Strings

题意

给定 \(k\) 个区间，求有多少种长度为 \(n\) 的合法括号序列，满足每个区间也是合法括号序列。

题解

考虑两个相交的区间，可以分成三个区间，三个区间都满足是合法括号序列。

黑色是原本的，黄色是现在的。

考虑两个相包含的区间，被包含的区间是一部分，剩余部分是一部分。

红色部分要满足合法，黄色部分拼起来也要满足合法。

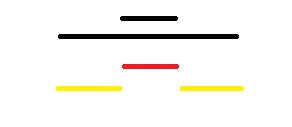
我们有一堆相交，相包含的区间交替出现，如果你要真的分割区间会是一个我不会的分讨。

我们考虑给每一个区间赋权值，相交部分的权值就异或起来。

在上面两种情况中权值异或后权值每一部分都不相同。

我们想要的是每一种区间的长度然后求卡特兰数，也就是每一种区间也就是每一个异或值对应的个数。

区间赋异或权值可以考虑差分序列，两端点赋了之后再前缀异或和得到原序列。

D. lMex Tree

题意

给定一棵 \(n\) 个结点的树，点有点权，点权为 0 或 1。你需要给一种指定点权的方案，使得每一条路径的点权 \(\operatorname{mex}\) 之和最大。

题解

考虑最优解是大多路径都是 2，少部分是 1或者 0。

那么我们记录距离所有路径都是 2 的情况缺失多少，我们要让缺失值最小。

设 \(f_{u, 0/1,i}\) 表示以 \(u\) 为根的子树，\(u\) 是 \(0/1\)，\(u\) 子树和 \(u\) 值相同的联通块大小为 \(i\) 。

\(f\) 初始值就是 \(f_{u,0,1} = 1,f_{u,1,1} = 2\) 。

本身到本身有贡献。

转移方程就是

\[f_{u,0,j} = \min(f_{u,0,j} + \min_{k=1}^{siz[v]}f_{v,1,k}, \min_{k = 1}^{siz[v]}(f_{u,0,j - k} + f_{v,0,k}+(j-k)\times k)\\ f_{u,1,j} = \min(f_{u,1,j} + \min_{k=1}^{siz[v]}f_{v,0,k}, \min_{k = 1}^{siz[v]}(f_{u,1,j - k} + f_{v,1,k}+2\times(j-k)\times k) \]

这样是 \(O(n^2)\) 的，我们怎么优化呢？

优化

我们考虑设每个子树大小为 \(siz\) ，最优情况联通块大小不超过 \(\sqrt {2n}\) 。

因为我们可以发现一种比较优秀的情况是黑白染色，这时候缺失值最多为 \(2n\) 。

当联通块大小为 \(x\) 时，缺失值最少是 \(x^2\) ，当联通块大小 \(\ge \sqrt {2n}\) 时候一定不够优秀。