PERIODNI - Periodni 题解 & 笛卡尔树讲解 & 树状背包讲解
PERIODNI - Periodni 题解 & 笛卡尔树讲解 & 树状背包讲解
前置知识笛卡尔树
笛卡尔树每个节点具有标号和 \(w_i\) ，两个属性 ，标号满足二叉搜索树的性质，而 \(w_i\) 满足小根堆的性质。
可以证明，给你标号和 \(w_i\) ，有且仅有一种形状的树满足笛卡尔树的性质。
构造笛卡尔树
这里提供一种最优秀的 O(n) 做法。
第一步，如果 \(w\) 和编号都是递增的按照编号将节点一个个挂上去，构造一条右链。形如：
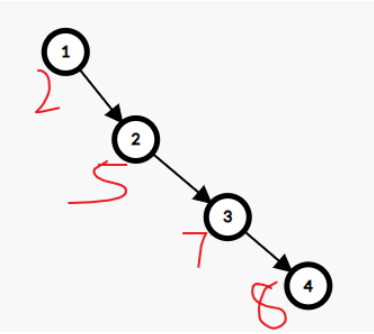
设当前节点为 \(i\) ，这条链的末尾节点为 \(t\)，当\(w_i < w_t\) ，在这条链上找一个 \(w_j\le w_i\) 作为节点 \(j\) 的右儿子，节点 \(j\) 本身的右儿子变成了节点 \(i\) 的左儿子。
例如，我们现在插入一个 \(w = 6\) 的点：
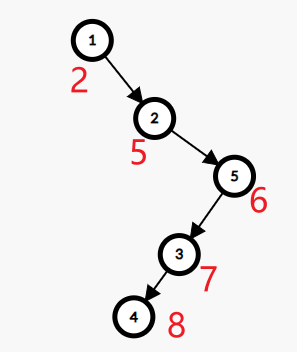
现在这个右链就变成了 \(1\rightarrow2\rightarrow5\) 这条链。
一直进行这样的操作就可以了。
但如果真的直接建树的话复杂度期望 \(O(n\log n)\) 甚至可以被卡成 \(O(n^2)\) 。（虽然可以过这个题）
所以我们用单调栈模拟实现。
单调栈实现
我们单调栈里面装的东西就是模拟这个右链。
当进入一个节点 a
-
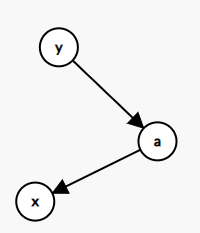
令这个节点在栈中弹出的最后一个节点是 x ，那么 a 的左儿子为 x。
-
令这个节点在栈中的下面一个的节点是 y ，那么 y 的右儿子为 a。
可以结合下面图和上面的构造理解一下。
代码
void input(){
cin>>n>>m;
for(int i = 1; i <= n; ++i){
cin>>v[i];
while(top && s[top].v > v[i]){
--top;
if((!top) || (top && s[top].v <= v[i])){
tr[i].ls = s[top + 1].num;
}
}
if(top)tr[s[top].num].rs = i;
s[++top] = (node){i,v[i]};
}
for(int i = 1;i <= n; ++i){
jl[tr[i].ls] = 1;
jl[tr[i].rs] = 1;
}
for(int i = 1;i <= n; ++i){
if(!jl[i]) rt = i;
}
}
题目
[题面](PERIODNI - Periodni - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
解析
建模
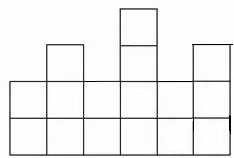
我们把这个奇怪的图形看出几个矩形拼接而成，把每个矩形标号。
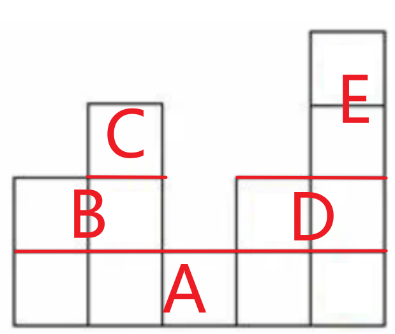
我们用每个矩形最矮的那一列来代表这个矩形
例如矩形 B 由 1,2 列构成，最矮的是 2 列，用 2 代替，类似的 D 用 4 来代替。
就变成了：
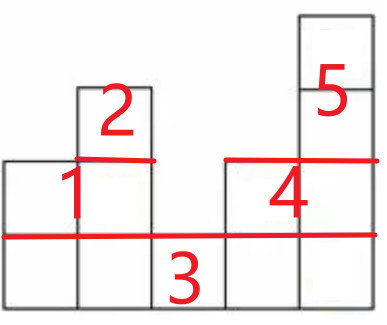
这像是一个树的结构，把他画出来看看。
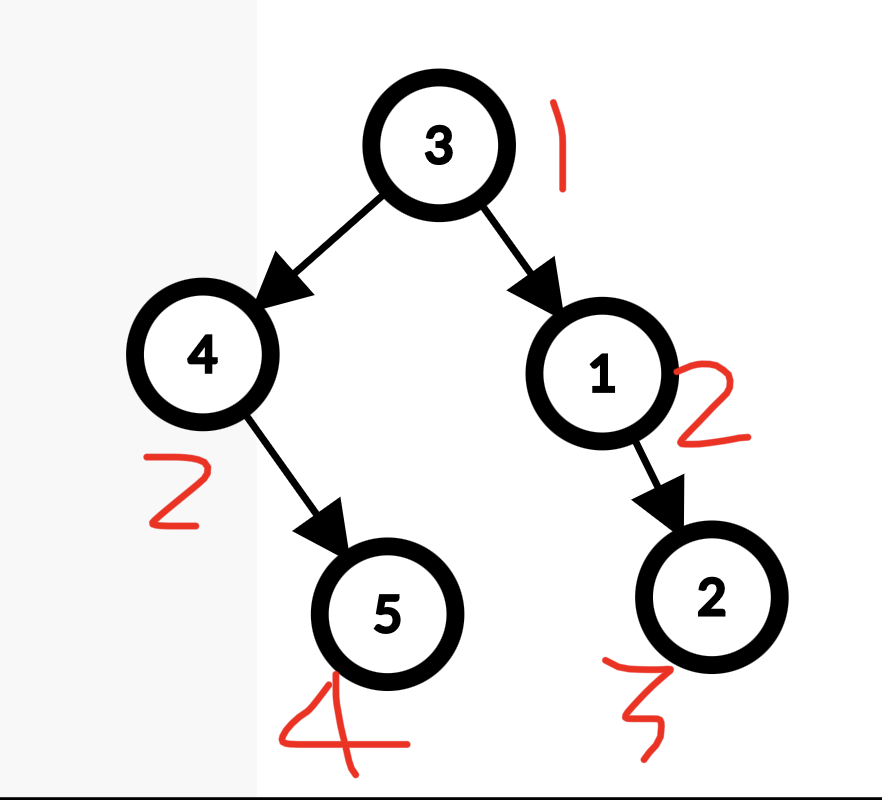
把当前行的高度作为 \(w\)， 好像是笛卡尔树，我们来证明一下。
首先，儿子节点的高度一定比父亲节点高，\(w\) 一定更大，一定满足小根堆的性质。
按照左边左儿子，右边右儿子的规律建的树，一定满足二叉搜索树的性质。
容易观察到两个性质：
-
某矩阵所代表 \(i\) 和 \(fa_i\)的高度差就是矩阵的长度。
-
以 \(i\) 为根的子树大小就是矩阵的宽度。
当时我有这样的疑惑，如果树长这样有好像有 3 个儿子，阁下该如何应对。
我们把这个笛卡尔树画出来。
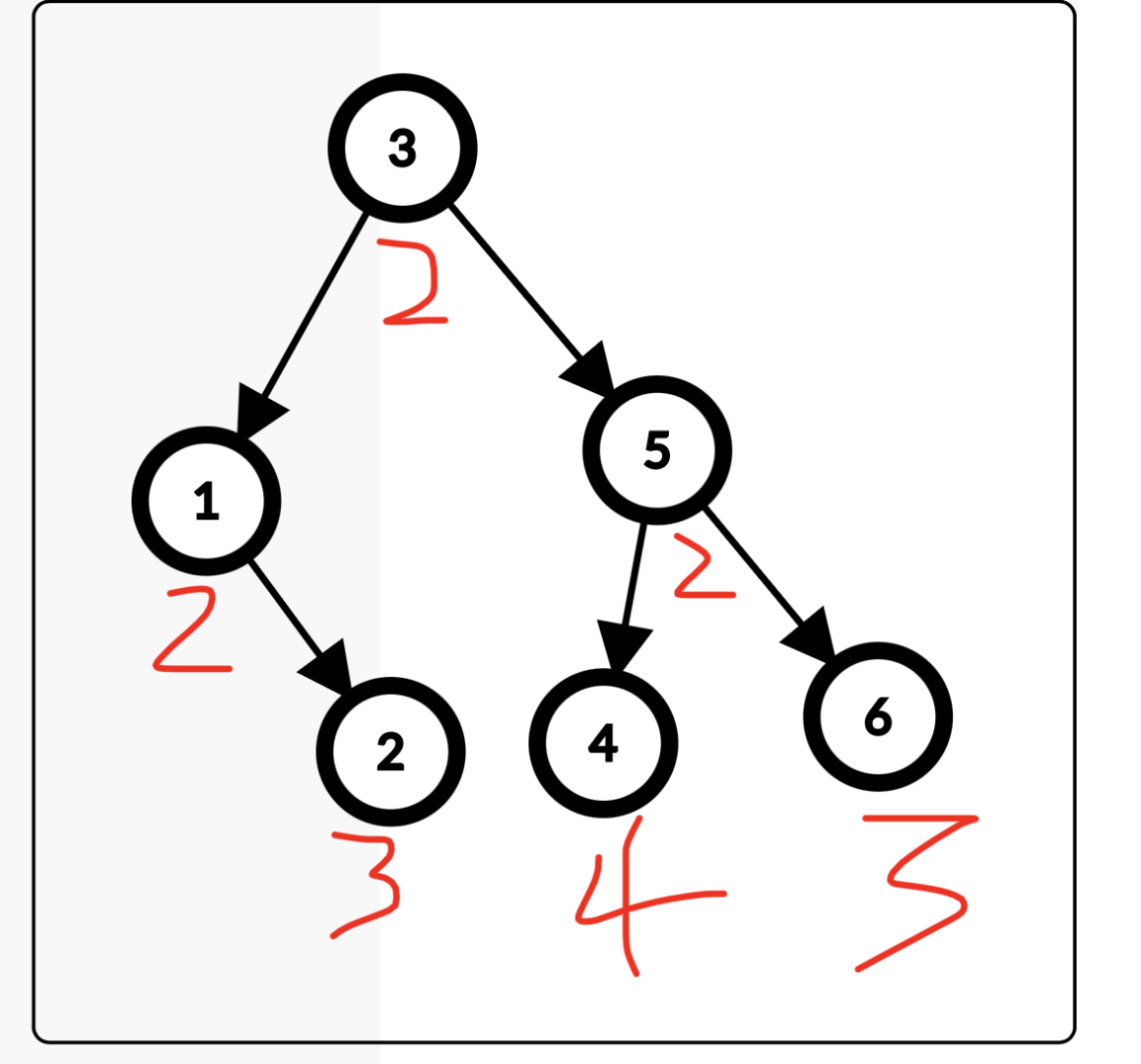
惊奇的发现它还是满足上面说的性质。
直接建树就行了。
树上背包
我们用树上背包 dp 。设 \(f[i][j]\) 表示以 i 根的子树的所有矩形中放了 j 个点的方案数。
方程
最后还要计算当前矩形放数字的方案数。
总的来说，先把左儿子放入更新，再把右儿子放入更新，最后用自己更新。
这是什么意思？
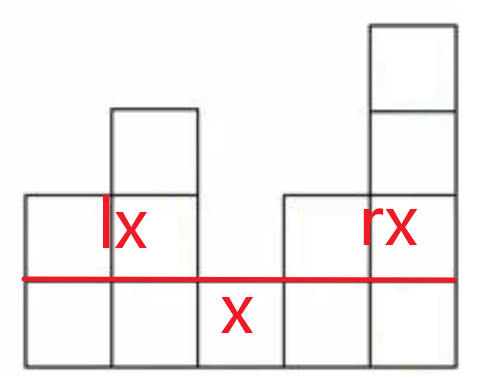
例子：假设现在我们考虑到 x，x 左儿子放 0,1,2 个，x 右儿子放 0,1,2 个，那在 x 区域就可以放 0,1,2,3,4 个。
树上背包的思想和背包很像，其实他省略了一维 k 表示当前考虑了 \(1\sim k\) 的儿子节点得到的结果，就像背包中我们省略了一维当前考虑了 \(1\sim i\) 的物品。
那么如果当前矩阵是 \(n\times m\) 的，选 \(k\) 个点，方案数是多少呢？
选 k 行 k 列，然后排列，显然：
一定记住倒序枚举，省去了子树一维，注意枚举边界。
