FFT&NTT
FFT快速傅里叶变换<NTT
FFT和NTT是 \(O(nlogn)\) 处理两个多项式相乘的算法（FFT<NTT）
前置知识
复数
一个复数可以表示为
我们把他看做平面上的一个点，横轴代表实数部分，纵轴代表虚数部分
这个点就是 \((a,b)\)
我们把它放在极坐标上
[没事，不会极坐标这里有](极坐标系 - 知乎 (zhihu.com))
令\(\theta = \arctan{\frac a b} , x=\sqrt {a^2+b^2}\)
那么这个点就是 \((x,\theta)\)
则有
虚数变为了
由欧拉公式得(欧拉公式)
这样任意一个虚数可以表示成这样
以上是复数前置知识
正式FFT
单位根
下文中，默认\(n\) 为 \(2\) 的正整数次幂
在复平面上，以原点为圆心，\(1\) 为半径作圆，所得的圆叫单位圆。以圆点为起点，圆的 \(n\) 等分点为终点，做 \(n\) 个向量，设幅角为正且最小的向量对应的复数为 \(\omega_n^0\) ，称为 \(n\) 次单位根，n代表长度。
根据复数乘法的运算法则，其余 \(n−1\) 个复数为 \(\omega_n^1,\omega_n^2,…,\omega_n^{n-1}\)
上面是我在别的地方看到的内容，学习FFT的时候我一直不太懂上面的部分，我今天用一个更加简单的方式让大家理解这部分内容
我们本来的多项式是这样的：
因为复数\(\omega\)有一些特殊性质，我们需要用，并且我们把 \(x\) 直接替换 \(\omega\) 是没有关系的
所以就变成了：
\(\omega_1,\omega_2,\omega_3,...,\omega_n\)不是一样的数，下面的n代表当前数列长度，算法里面不同时候用不同的，这个和他的性质有关系。
说了这么久 \(\omega\) 的性质，到底是什么性质呢？
通过欧拉定理
证明一些单位根性质，下面需要用
\(1.\omega_n^0=\omega_n^n=1\)
这显而易见。
\(2.\omega_n^{k+\frac n 2}=-\omega_n^k\)
证明：
\(3.\omega_{2n}^{2k}=\omega_n^k\)
证明：
\(4.\sum_{i=0}^{n-1}(\omega_n^k)^i=0\)
证明：
第一步是根据等比数列求和公式：
傅里叶变换(学名不重要)
他的原理就是把系数表示法变成点值表示法，点值乘起来时间是O(n)，再转为系数表示法
我们取的点是\(\omega_n^0,\omega_n^1,...,\omega_n^{n-1}\)
所对应的函数值我们定义一个函数 \(h\) 表示
\(h(\omega_n^k)=c_0+c_1(\omega_n^k)^1+c_1(\omega_n^{k})^2+...+c_{n-1}(\omega_n^{k})^{n-1}\)
所以我们的步骤就变成了这样
那我们应该如何在\(O(nlogn)\)的复杂度内算出 \(h\) 函数呢？
求 \(h()\)
我们把h函数分成偶数项和奇数项两部分
通过可以推出\(\omega_{2n}^{2k}=\omega_n^k\)
\( h(\omega_n^k)=h_{0}(\omega_{\frac n 2}^{k})+\omega_n^k h_{1}(\omega_{\frac n 2}^{k}) \)
同理，将 \(\omega_n^{ k+\frac n2}\) 代入得
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{ 2k+n})+\omega_n^{k+\frac n2}h_1(\omega_n^{ 2k+n})\)
因为\(\omega_n^{k+\frac n2}=-\omega_n^{k}\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{2k}\omega_n^{n})-\omega_n^{k}h_1(\omega_n^{2k}\omega_n^{n})\)
因为\(\omega_n^n=1\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{2k})-\omega_n^{k}h_1(\omega_n^{2k})\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_{\frac n2}^{k})-\omega_n^{k}h_1(\omega_{\frac n2}^{k})\)
发现 \(h(\omega_n^{k})\) 和 \(h(\omega_n^{ k+\frac n2})\) 刚好是一加一减
我们在枚举第一个式子的时候也可以求出第二个式子的值啦
\(n\) 代表当前数列长度，每次减半，所以是\(log(n)\)
你是不是还是脑子里依托浆糊，我们来搞一个例子推一下(一个大括号里的前一个式子是我们需要的式子，后一个是顺便求出的)
假设我们求\(h(\omega_8^1)\)这个数列一共八位
\(h_{00}\) 代表偶数中的偶数，也就是这个数二进制下的末尾两位是不是00
继续推下去
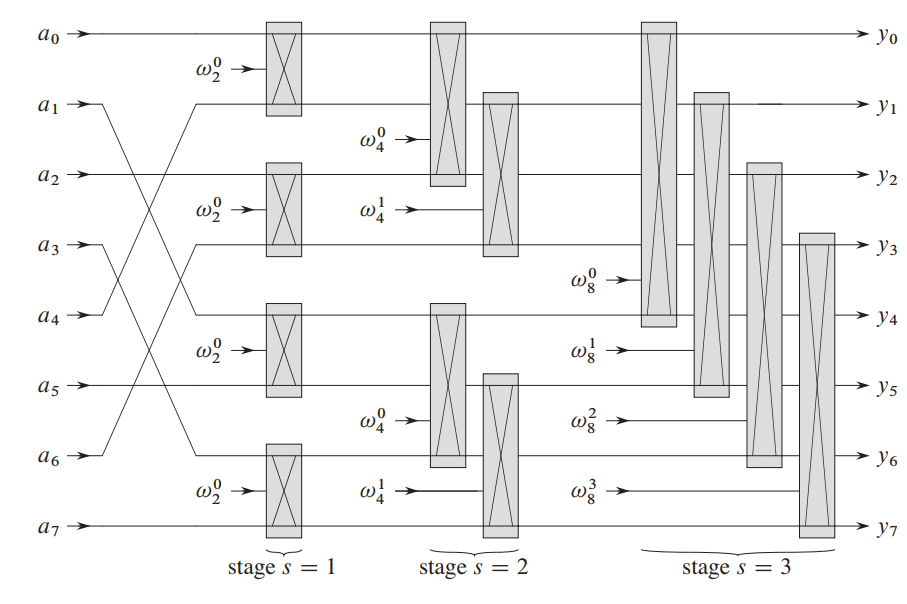
这是一种递归，我讨厌递归，他很慢，所以我们考虑能不能把递归换成递推
递推部分：
看了这个图你一定可以懂、
规则：
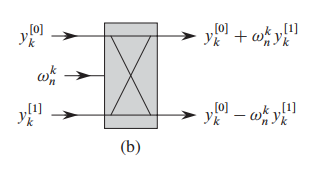
当\(n=8\)具体操作（配合代码食用更佳）
我们还有一步就是把 \(h\) 函数转回去
我们考虑这样做：
我们把 \(h\) 放入一个数列
\(<h(\omega_n^1),h(\omega_n^2),h(\omega_n^3),...,h(\omega_n^n)>\)
把这个数列在进行一次傅里叶变换，得出这个序列的离散傅里叶级数，但是是负的
你成功学会了FFT，当然NTT比他好十倍甚至九倍，也是一样简单
NTT
代码
FFT代码
#include<bits/stdc++.h>
#define llf double
using namespace std;
const llf PI=acos(-1);
const int N=5e6+10;
int n,m,x,rev[N],logO=0,mn;
struct Cmop{
llf x,y;
}a[N],b[N],c[N];
Cmop operator + (Cmop a ,Cmop b){return {a.x+b.x,a.y+b.y};}
Cmop operator - (Cmop a ,Cmop b){return {a.x-b.x,a.y-b.y};}
Cmop operator * (Cmop a ,Cmop b){return {a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(Cmop *c,int len,int op){
for(int i = 0;i < len; ++i)if(i < rev[i]) swap(c[i], c[rev[i]]);
for(int k = 1;k < len;k <<= 1){//当前有多少行
Cmop omega = {cos(PI / k),sin(PI / k * op)};
for(int j = 0; j < len;j += (k << 1)){//j列和j+1列操作
Cmop o = {1,0};
for(int i = 0; i < k; ++i){//把i行进行操作
Cmop u = c[i + j], v = o * c[i + j + k];
c[i + j] = u + v;
c[i + j + k] = u - v;
o = o * omega;
}
}
}
}
void input(){
scanf("%d%d", &n, &m);
for(int i = 0;i <= n; ++i){
scanf("%d", &x);
a[i] = {x*1.0, 0};
}
for(int i = 0;i <= m; ++i){
scanf("%d", &x);
b[i] = {x*1.0, 0};
}
}
void op(){
mn=1;
while(mn <= n+m) mn <<= 1, ++logO;
for(int i = 0;i < mn; ++i)rev[i] = (rev[i>>1] >> 1) | (( i & 1) << (logO-1));
FFT(a, mn, 1);
FFT(b, mn, 1);
for(int i = 0; i < mn; ++i){
c[i] = a[i] * b[i];
}
FFT(c, mn, -1);
for(int i = 0; i < mn; ++i){
c[i].x /= mn;
}
for(int i = 0; i <=m+n; ++i){
printf("%d ", (int)(c[i].x + 0.1));
}
}
int main(){
input();
op();
return 0;
}
NTT代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 4e6+10,MOD = 998244353,g = 3,revG = 332748118;
int n,m,rev[N],logO=0,mn;
ll a[N], b[N], c[N];
inline ll mpow(ll a,ll k){
ll ans = 1;
while(k){
if(k & 1) ans=(ans * a) % MOD;
a=(a * a) % MOD;
k >>= 1;
}
return ans%MOD;
}
inline void FFT(ll *c,int len,int op){
for(int i = 0;i < len; ++i)if(i < rev[i]) swap(c[i], c[rev[i]]);
for(int k = 1;k < len;k <<= 1){//当前有多少行
ll g_k = mpow(op == 1 ? g : revG , (MOD-1) / (k << 1));
for(int j = 0; j < len;j += (k << 1)){//j列和j+1列操作
ll o = 1;
for(int i = 0; i < k; ++i){//把i行进行操作
ll u = c[i + j], v = o * c[i + j + k] % MOD;
c[i + j] = (u + v) % MOD;
c[i + j + k] =(u - v + MOD) % MOD;
o = o * g_k % MOD;
}
}
}
inline void input(){
scanf("%d%d", &n, &m);
for(int i = 0;i <= n; ++i){
scanf("%lld", &a[i]);
}
for(int i = 0;i <= m; ++i){
scanf("%lld", &b[i]);
}
}
inline void op(){
mn=1;
while(mn <= n+m) mn <<= 1, ++logO;
for(int i = 0;i < mn; ++i)rev[i] = (rev[i>>1] >> 1) | (( i & 1) << (logO-1));
FFT(a, mn, 1);
FFT(b, mn, 1);
for(int i = 0; i < mn; ++i){
c[i] = a[i] * b[i] % MOD;
}
FFT(c, mn, -1);
ll inv = mpow(mn, MOD-2);
for(int i = 0; i <=m + n; ++i){
printf("%lld ", c[i]*inv%MOD);
}
}
int main(){
input();
op();
return 0;
}
