js二叉树

二叉树

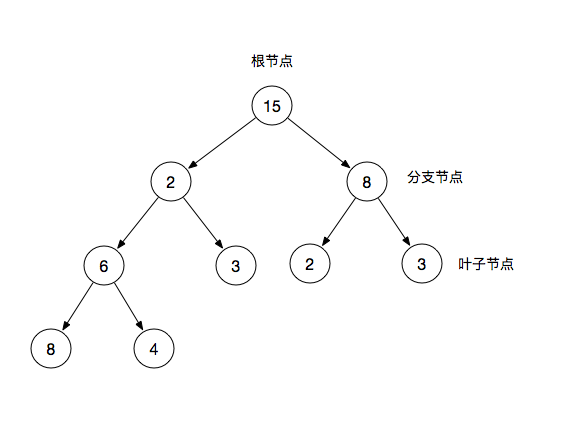
二叉树(Binary Tree)是一种树形结构，它的特点是每个节点最多只有两个分支节点，一棵二叉树通常由根节点，分支节点，叶子节点组成。而每个分支节点也常常被称作为一棵子树。

• 根节点：二叉树最顶层的节点

• 分支节点：除了根节点以外且拥有叶子节点

• 叶子节点：除了自身，没有其他子节点

常用术语

在二叉树中，我们常常还会用父节点和子节点来描述，比如图中2为6和3的父节点，反之6和3是2子节点

二叉树的三个性质

1. 在二叉树的第i层上，至多有2^i-1个节点

   • i=1时，只有一个根节点，2^(i-1) = 2^0 = 1
     2.. *深度为k的二叉树至多有2^k-1个节点

   • i=2时，2^k-1 = 2^2 - 1 = 3个节点

2. 对任何一棵二叉树T，如果总结点数为n0，度为2(子树数目为2)的节点数为n2,则n0=n2+1
   

树和二叉树的三个主要差别

• 树的节点个数至少为1，而二叉树的节点个数可以为0
• 树中节点的最大度数(节点数量)没有限制,而二叉树的节点的最大度数为2
• js二叉树树的节点没有左右之分，而二叉树的节点有左右之分

二叉树分类

二叉树分为完全二叉树(complete binary tree)和满二叉树(full binary tree)

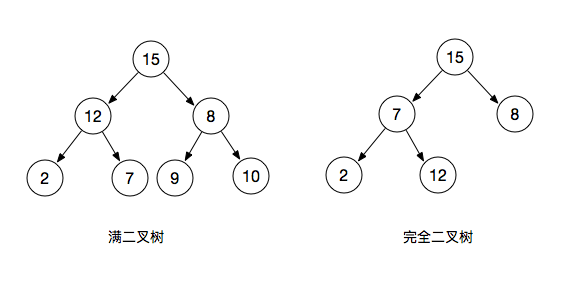
• 满二叉树：一棵深度为k且有2^k - 1个节点的二叉树称为满二叉树完全二叉树：
• 完全二叉树是指最后一层左边是满的，右边可能满也可能不满，然后其余层都是满的二叉树称为完全二叉树(满二叉树也是一种完全二叉树)

二叉搜索树

二叉搜索树满足以下的几个性质：

• 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 任意节点的左、右子树也需要满足左边小右边大的性质

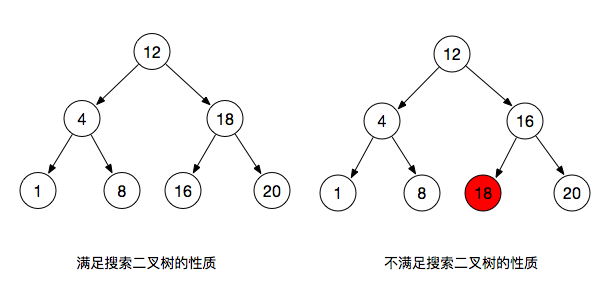
我们来举个例子来深入理解以下

一组数据：12,4,18,1,8,16,20
由下图可以看出，左边的图满足了二叉树的性质，它的每个左子节点都小于父节点，右子节点大于其父节点，同时左子树的节点都小于根节点，右子树的节点都大于根节点

遍历

• 中序遍历(inorder)：

先遍历左节点，再遍历自己，最后遍历右节点，输出的刚好是有序的列表

• 前序遍历(preorder)：

先自己，再遍历左节点，最后遍历右节点

• 后序遍历(postorder)：

先左节点，再右节点，最后自己

(剑指offer p4)

1.输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
function reConstructBinaryTree(pre, vin) {
    let result = null;
    if (pre.length > 1) {
        let index = vin.indexOf(pre[0]);
        let vinLeft = vin.slice(0, index);
        let vinRight = vin.slice(index + 1, vin.length);
        let val = pre.shift();
        let preLeft = pre.slice(0, vinLeft.length);
        let preRight = pre.slice(vinLeft.length, pre.length);
        result = {
            val: val,
            left: reConstructBinaryTree(preLeft, vinLeft),
            right: reConstructBinaryTree(preRight, vinRight)
        }
    } else if (pre.length === 1) {
        return result = {
            val: pre[0],
            left: null,
            right: null
        }
    }
    return result;
}

二叉树镜像

操作给定的二叉树，将其变换为源二叉树的镜像。

二叉树的镜像定义：源二叉树

            8
           /  \
          6   10
         / \  / \
        5  7 9 11
        镜像二叉树
            8
           /  \
          10   6
         / \  / \
        11 9 7  5

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
function Mirror(root)
{
    // write code here
    if(root === null) {
        return;
    }
    var temp = root.left;
    root.left = root.right;
    root.right = temp;
    Mirror(root.left);
    Mirror(root.right);
}