第六届福建省大学生程序设计竞赛不完全题解
昨天自己队做了一下第六届福建省赛,感觉有些蒙,赛后补了几道题,能力有限,一共只出A了7道题
A题 Super Mobile Charger
题目链接
http://acm.fzu.edu.cn/problem.php?pid=2212
水题

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int a[10005]; int b[10005]; int main() { int t,n,m,f; cin>>t; while(t--) { f=0; cin>>n>>m; for(int i=0;i<n;i++) { cin>>a[i]; b[i]=100-a[i]; } sort(b,b+n); for(int i=0;i<n;i++) { if(m>=b[i]) f++; m=m-b[i]; } cout<<f<<endl; } }
B题 Common Tangents(两圆之间的公共切线)
题目链接
http://acm.fzu.edu.cn/problem.php?pid=2213
题意:给出两个圆心和半径求两圆的公共切线数量
模板题,比赛时没有用模板,直接数学模拟;

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int main() { int t; int x1,y1,r1,x2,y2,r2; cin>>t; while(t--) { cin>>x1>>y1>>r1>>x2>>y2>>r2; int p=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2); int R=abs(r1-r2); int r=r1+r2; if(p==0&&r1 == r2) cout<<"-1"<<endl; else if(p==r*r) cout<<"3"<<endl; else if(p==R*R) cout<<"1"<<endl; else if(p>=R*R&&p<=r*r) cout<<"2"<<endl; else if(p>r*r) cout<<"4"<<endl; else cout<<"0"<<endl; } return 0; }
下面是套模板代码:

#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> using namespace std; struct Point{ double x,y; Point(double x = 0,double y = 0):x(x),y(y){} // 构造函数,方便代码编写 }; typedef Point Vector; //从程序实现上,Vector只是Point的别名 struct Circle{ Point c; double r; Circle(Point c,double r):c(c),r(r){} Point getPoint(double a){ return Point(c.x+cos(a)*r,c.y+sin(a)*r); } }; //返回切线的条数。-1表示无穷条切线 //a[i]和b[i]分别是第i条切线在圆A和圆B上的切点 int getTangents(Circle A,Circle B){ int cnt = 0; if(A.r < B.r) swap(A,B); int d2 = (A.c.x-B.c.x)*(A.c.x-B.c.x)+(A.c.y-B.c.y)*(A.c.y-B.c.y); int rdiff = A.r-B.r; int rsum = A.r+B.r; if(d2 < rdiff*rdiff) return 0; //内含 if(d2==0 && A.r==B.r) return -1; //无限条切线 if(d2 == rdiff*rdiff){//内切,1条切线 return 1; } //有外公切线 cnt += 2; if(d2 == rsum*rsum){//一条公切线 ++cnt; } else if(d2 > rsum*rsum){//两条公切线 cnt += 2; } return cnt; } int main(){ int T; scanf("%d",&T); while(T--){ Point p1,p2; double r1,r2; scanf("%lf%lf%lf",&p1.x,&p1.y,&r1); Circle c1(p1,r1); scanf("%lf%lf%lf",&p2.x,&p2.y,&r2); Circle c2(p2,r2); printf("%d\n",getTangents(c1,c2)); } return 0; }
C题 Knapsack problem(动态规划)
题目链接
http://acm.fzu.edu.cn/problem.php?pid=2214
题意不多说,01背包问题,二维一维都可以解决,比赛时一直卡在二维上。。。用了一维才A了
后来别人指点才改正了小错误。。
dp[i]表示总价值为i的最小重量是多少。dp[j] = min(dp[j] , dp[j-v[i]]+wl[i])
一维代码:

明显得到背包问题,f[i]表示的是有i价值的时候的最小重量 #include<iostream> #include<cstdio> #include<cstring> using namespace std; int f[5005]; int sum; int v[505],w[505]; void init() { for(int i=1; i<=sum; i++) f[i]=1000000010; } int main() { int T; scanf("%d",&T); while(T--) { int n,B; sum=0; scanf("%d%d",&n,&B); for(int i=1; i<=n; i++) { cin>>w[i]>>v[i]; sum+=v[i]; } init(); f[0]=0; for(int i=1; i<=n; i++) { for(int j=sum; j>=0; j--) if(j>=v[i]) f[j]=min(f[j],f[j-v[i]]+w[i]); } //for(int i=0;i<=sum;i++) cout<<f[i]<<" "<<i<<endl; int d=0; for(int i=sum; i>=0; i--) { if(f[i]<=B) { cout<<i<<endl;d=1; } if(d==1) break; } } return 0; }
二维代码:

#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int INF = 1000000010; int v[505]; int w[505]; int f[505][5005]; int main() { int t; cin >> t; while(t--) { int n, b; int sum = 0; cin >> n >> b; for(int i = 1; i <= n; i++) { scanf("%d %d", &w[i], &v[i]); sum += v[i]; } for(int i=0; i<=n; i++) for(int j = 0; j <= sum; j++) f[i][j] = INF; for(int i = 0; i <= n; i++) f[i][0] = 0; for(int i = 1; i <= n; i++) { for(int j = sum; j >= 0; j--) { if(j >= v[i]) f[i][j] = min(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); else f[i][j] = f[i - 1][j]; } } for(int i = sum; i >= 0; i--) { if(f[n][i] <= b) { cout << i << endl; break; } } } return 0; }
E题 The Longest Straight
题目链接:
http://acm.fzu.edu.cn/problem.php?pid=2216
题意:给n个0~m之间的数,如果是0,那么0可以变为任意的一个1~m之间的一个数。从中选出若干个数,使构成一个连续的序列。问能构成的最长序列的长度为多少?
标记出现过的数字,并统计0的个数cnt,
预处理数组num[] ,num[i]为范围[1,i]内需要0的数量,那么num[r]-num[l-1]即为范围[l,r]内需要0的数量,那么该连续上升序列长度为r-l+1。
这个不难理解。枚举连续序列的左端点,二分枚举二分序列的右端点
在需要填充的0的数量小于等于k的情况下,遍历所有范围[l,r]的连续上升序列长度,记录最大值即可。
在确定左端点l的情况下,二分查找num[r]-num[l-1]+k>=r-l+1的右端点r,然后记录最大长度即可。

# include<iostream> # include<cstdio> # include<cstring> # include<algorithm> using namespace std; int f[100005]; int n,m,x; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); memset(f,0,sizeof(f)); int k=0; for(int i=1; i<=n; ++i) { scanf("%d",&x); if(x) f[x]=1; else ++k; } for(int i=1; i<=m; i++) f[i]+=f[i-1]; int ans=0; for(int i=1; i<=m; i++) { int l=i,r=m; while(l<=r) { int mid=(l+r)>>1; if(f[mid]-f[i-1]+k>=mid-i+1) { ans=max(ans,mid-i+1); l=mid+1; } else r=mid-1; } } printf("%d\n",ans); } return 0; }
另一种时间复杂度(O(n))

#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; const int maxn = 100005; int n, m, zero; int num[maxn]; //num表示从1到i成为顺子所需鬼牌的个数 int card[maxn]; int main() { int T; scanf("%d", &T); while (T--) { zero = 0; memset(num, 0, sizeof(num)); memset(card, 0, sizeof(card)); scanf("%d%d", &n, &m); for (int i = 0; i < n; i++) { int x; scanf("%d", &x); if (!x) zero++; else card[x] = 1; } for (int i = 1; i <= m; i++) num[i] = num[i - 1] + (1-card[i]); int ans = 0; for (int i = 1; i <= m; i++) { int k = upper_bound(num + i, num + m + 1, zero + num[i-1]) - (num + i); ans = max(ans, k); } printf("%d\n", ans); } return 0; }
G题 Simple String Problem(状态压缩dp)
题目链接:
http://acm.fzu.edu.cn/problem.php?pid=2218
题意:有一个长度为n的由字母表前k个字母组成的字符串,取任意两个该字符串的子串s1和s2,要求s1和s2中相互没有相同字母,并且s1和s2长度的乘积要尽可能大,输出该乘积。
状压!好像也可以直接枚举或者贪心
巩固了一下状压。。。感觉以前不怎么懂 啊
首先拿到一个字符串很难处理,这时候需要进行状态压缩,每一个子串都可以用由01组成的二进制来表示状态,1代表相应位置上有字母,0则没有。
举个例子:a->1,b->10,c->100,acaa->101,abcaa->111。
k最大值为16,这样我们最多就只有2^16种状态,有了状态值判断两个子串是否有相同字符也就很容易了,只要两个子串的状态值按位与结果为0即没有相同字符,这点很好验证,那么最终答案也为dp[x]*dp[补(x)],这样大概做法就确定下来了。
首先先进行一遍预处理,记录每种状态字符串的最长长度。
然后进行一遍DP,dp[i]表示集合为S或S的子集的子串的最长长度。如ac和abc,ac为abc的子集,ac状态值为101即5,abc状态值为111即7,这时候ac为abc子集,转移方程式为dp[7]=max(dp[5],dp[7]);
补充:如”aabcaaaaaa”,此时只含有字符ab子串的状态值为3,只含有字符a子串的状态值为1,第一遍预处理后,只含有字符ab最长子串长度为dp[3]=3,而只含有字符a最长子串长度为dp[1]=6。a为ab的子集,显然dp[3]需要更新为6。
最后直接枚举所有状态与该状态互补的状态子串最长长度的乘积,最大值就是最终的答案。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int dp[1<<16]; char s[2000+5]; int t,n,k; int main() { cin>>t; while(t--) { memset(dp,0,sizeof(dp)); scanf("%d%d%s",&n,&k,s); int z=(1<<k); for(int i=0; i<n; i++)//初始化dp数组,记录每种状态字符串的最长长度 { int x=0; for(int j=i; j<n; j++) { int f=1<<(s[j]-'a'); x|=f; dp[x]=max(dp[x],j-i+1); } } for(int i=1; i<z; i++)//更新dp[i],dp[i]表示集合为S或S的子集的子串的最长长度。 for(int j=0; j<k; j++) { int y=1<<j; if(i&y) dp[i]=max(dp[i],dp[i-y]); } int cnt=0; for(int i=1; i<z; i++)//遍历所有状态和其补集的长度乘积,记录最大值。 cnt=max(cnt,dp[i]*dp[z-i-1]); cout<<cnt<<endl; } return 0; }
H题 StarCraft(哈夫曼树+优先队列)
题目链接:
http://acm.fzu.edu.cn/problem.php?pid=2219
这道题。。比赛的时候听队友讲题意,听的有点晕,后来补题发现是星际争霸游戏题目,这个游戏玩了四年,突然好怀念,又下了准备玩两把。。
题意:玩过的一看就知道了,虫族建筑需要农民做祭品,一个虫卵可以生出两个农民。。。嗯不多说了
类似哈夫曼树的合并方式,对于当个农民来说,算上分裂技能,建造是不断两两并行的,建造时间越小,合并的价值就越小。
合并后的时间去被合并两者的较大值+k。初始农民的数量m就是合并的终点。
其实就是给你一堆数字,每次把次小值+k,再删除当前最小值,直到剩下m个数字。
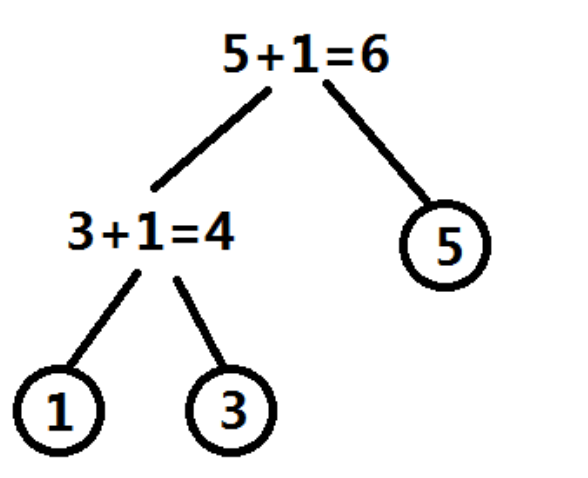
这里要用到一个越小的整数优先级越大的优先队列= =‘,相当方便。

#include<cstdio> #include<queue> #include<iostream> using namespace std; priority_queue<int, vector<int>, greater<int> > pq;//越小的整数优先级越大的优先队列= =‘ int main() { int t, n, m, k, x; scanf("%d", &t); while (t--) { scanf("%d%d%d", &n, &m, &k); for (int i = 0; i < n; i++) scanf("%d", &x), pq.push(x); while (n > m) { pq.pop(); pq.push(pq.top() + k); pq.pop(); --n; } while (pq.size() != 1) pq.pop(); printf("%d\n", pq.top()); pq.pop(); } return 0; }
J题 RunningMan
题目链接:
http://acm.fzu.edu.cn/problem.php?pid=2221
水题,只要保证R队任意两轮至少赢下一轮就可以了
解题思路:现在将R组分为3队,人数为x,y,z。那么如果满足题意,则R组中每两个队伍都必须获胜,另外一队必输。
需同时满足: x+y >= m-1 表示:x,y两队胜,z队输。z队队员0个人跟O组除了跟x,y对战的另一队人数为1人对战,失败。
x+z >= m-1
y+z >= m-1
x+y+z = n
联立方程组,解得 n >= 3*(m-1)/2

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int main() { int t; scanf("%d",&t); double n,m; while(t--) { scanf("%lf%lf",&n,&m); if(n >= 3*(m-1)/2) puts("Yes"); else puts("No"); } return 0; }


