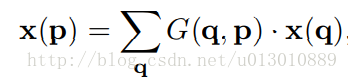【转】双线性插值

转自：

双线性插值(Bilinear Interpolation)

 

最近用到插值算法，使用三次样条插值时仿真速度太慢，于是采用算法简单的线性插值。本篇主要介绍一下双线性插值的实现方法。

1. 线性插值

已知坐标 (x₀, y₀) 与 (x₁, y₁)，要得到 [x₀, x₁] 区间内某一位置 x 在直线上的值。

由于 x 值已知，所以可以从公式得到 y 的值

已知 y 求 x 的过程与以上过程相同，只是 x 与 y 要进行交换。

 

2. 双线性插值(Bilinear Interpolation)

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

图中：红色的数据点与待插值得到的绿色点

假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q₁₁ = (x₁, y₁)、Q₁₂ = (x₁, y₂), Q₂₁ = (x₂, y₁) 以及 Q₂₂ = (x₂, y₂) 四个点的值。

首先在 x 方向进行线性插值，得到

然后在 y 方向进行线性插值，得到

这样就得到所要的结果 f(x, y)，

双线性插值在三维空间的延伸是三线性插值。

双线性插值本质上就是在两个方向上做线性插值。
x§的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个点的像素值x§: (i+u,j+v) 可由坐标为 x(q1): (i,j)、x(q2): (i+1,j)、x(q3): (i,j+1)、x(q4): (i+1,j+1)所对应的周围四个像素的值决定

1. 先在x方向上做线性插值得到t1 t2的像素值
2. 再在y方向做线性插值最终得到x§的像素值
   最终公式:

f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) (一)

对应到可变形卷积上求x§


g(a, b) = max(0, 1 − |a − b|). q就是临近的4个点, p0,pn,∆pn都是二维坐标,可带入公式一