数据结构--主席树

可持久化线段树

静态区间第 \(k\) 小

给定 \(n\) 个整数构成的序列，将对于指定的闭区间查询其区间内的第 \(k\) 小值。

权值线段树

权值线段树就是对一个值域上值的个数进行维护的线段树。

举个栗子，对于1，1，2，3，3，3，4，4。

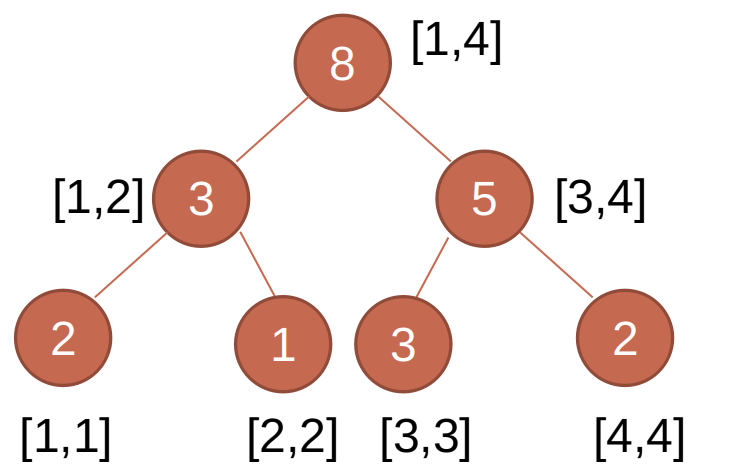
在权值线段树上如何求第k小的值？

显然如果左子树的值大于ｋ的话，那么答案就在左子树上，不然就在右子树上，而且是右子树第（k-左子树值）小。

主席树

我们对每个节点，都新建一颗权值线段树，不过我们保留一些不变的节点，只新建改变的了的节点。

对于询问[L,R]，每个root[i]节点所表示的值域都是[1,n]，

\(t[t[R].l].sum-t[t[L-1].l].sum\)表示的就是区间[L,R]内值域属于\([1,{n \over 2}]\)数的个数。

如果这个数大于k，那么表示答案落在值域\([1,{n \over 2}]\)，不然就表示答案落在值域\([{n \over 2},n]\)。

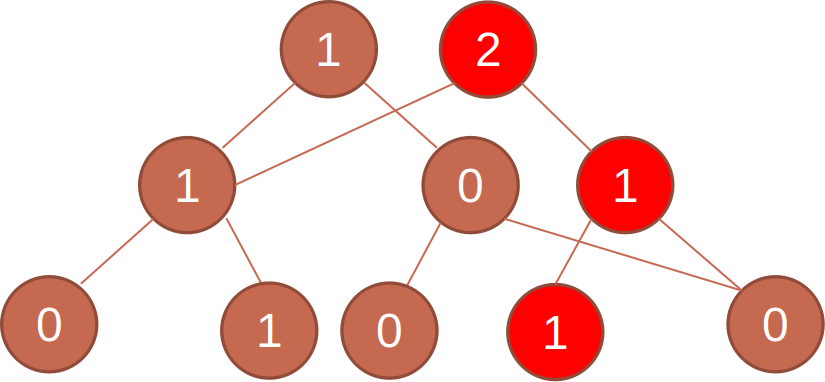
下图表示的是先插入一个２，再插入一个３之后的主席树。

code

#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define pii pair<int,int>
const int inf = 0x3f3f3f3f;
const int maxn = 201110;
const int M = 1e9+7;
int n,m;

int read()
{
    int x=0;
    char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
    return x;
}

int a[maxn];
vector<int> v;

struct node
{
    int l,r,sum;
}t[maxn*40];

int cnt,root[maxn];

int getid(int x)        //离散化
{
    return lower_bound(v.begin(),v.end(),x)-v.begin() + 1;
}

void insert(int l,int r,int pre,int &now,int p)         //当前插入的区间，pre表示要复制的点，now表示要创建的新节点
{
    t[++cnt] = t[pre];
    now = cnt;
    t[now].sum++;
    int mid = (l+r)/2;
    if(l == r) return;
    if(p <= mid) insert(l,mid,t[pre].l,t[now].l,p);
    else insert(mid+1,r,t[pre].r,t[now].r,p);
}

int query(int l,int r,int L,int R,int k)
{
    if(l == r) return l;
    int mid = (l+r)/2;
    int tmp = t[t[R].l].sum - t[t[L].l].sum;
    if(k <= tmp) return query(l,mid,t[L].l,t[R].l,k);
    else return query(mid+1,r,t[L].r,t[R].r,k-tmp);
}

signed main()
{
#ifdef ONLINE_JUDGE
#else
    freopen("data.in", "r", stdin);
#endif
    n = read(), m = read();
    for(int i = 1; i <= n; i++) 
    {
        v.push_back(a[i] = read());
    }
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    int sz = v.size();
    for(int i = 1; i <= n; i++) 
    {
        insert(1,sz,root[i-1],root[i],getid(a[i]));
    }
    int l,r,k;
    while(m--)
    {
        l = read(), r = read(), k = read();
        printf("%d\n",v[query(1,sz,root[l-1],root[r],k)-1]);
    }
    return 0;
}