dp--斜率dp

Problem Description

hdu3507
Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.

Input

There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.

Output

A single number, meaning the mininum cost to print the article.

Sample Input

5 5
5
9
5
7
5

Sample Output

230

Analysis of ideas

首先定义dp[i]表示i个字符的最小费用
状态转移方程\(dp[i] = min(dp[i],dp[j] + m + (sum[i]-sum[j])^2);\)
表示[j+1,i]组成新的一段,对于每一个i,枚举j,时间复杂度\(O(n^2)\)

mem(dp,inf);
dp[0] = 0;
for(int i = 1; i <= n; i++)
{
    for(int j = 0; j < i; j++)
    {
        dp[i] = min(dp[i],dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]));
    }
}

显然\(O(n^2)\)会超时,所以我们需要更快的方法

我们假设k<j,并且选择j的时候的决策比选择k的时候的决策要好,则满足

$dp[j]+m+(sum[i]-sum[j])^2 < dp[k]+m+(sum[i]-sum[k])^2$ 移项 ${(dp[j]+sum[j]^2)-(dp[k]-sum[k]^2) \over {2\times(sum[j]-sum[k])}} < sum[i]$ 我们把$dp[j]+sum[j]^2$看成$y_j$,把$2 \times sum[j]$看成$x_j$ 于是乎 ${y_j-y_k \over {x_j - x_k}} < sum[i]$ 所以,当满足上述式子的时候,从j转移会比从k转移要好

接下来,我们考虑这样一种情况

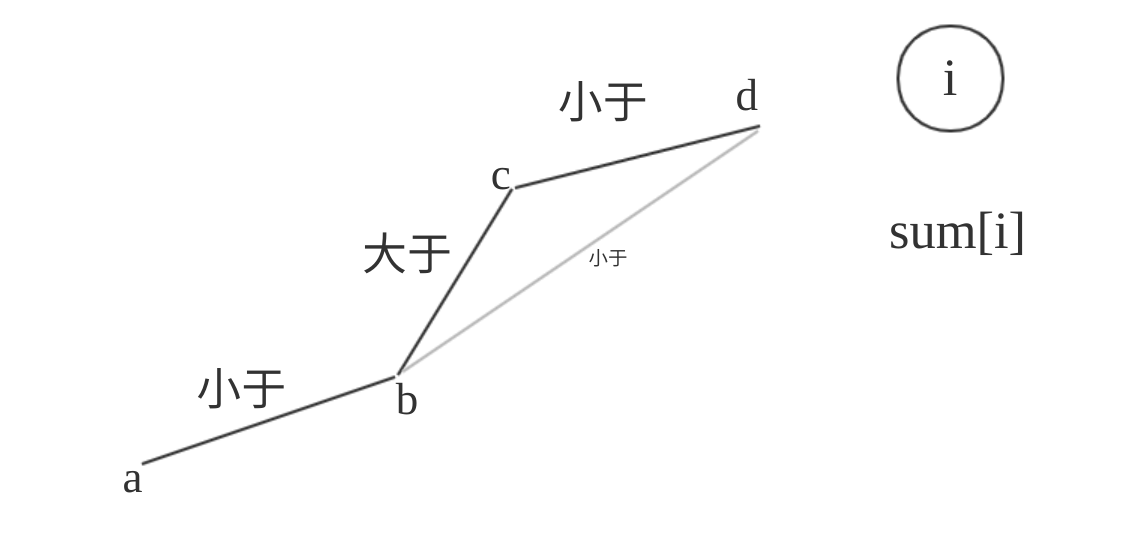
从b的决策显然优于a,而c的决策不会优于b,但是d才是最优解,所以我们需要把c删掉,不然就选不到最优解d(这一段看不懂的可以先看代码)
所以说队列里面的元素的斜率是递增的

Code

#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define cin(a) scanf("%d",&a)
#define pii pair<int,int>
#define ll long long
#define gcd __gcd
const int inf = 0x3f3f3f3f;
const int maxn = 501110;
const int M = 1e9+7;
int n,m,k,t;


int a[maxn];
ll sum[maxn];                   //前缀和
int q[maxn],head,rear;          //队列
ll dp[maxn];                    //dp[i]表示前i个的最小代价

ll getup(int j,int k)           //分母
{
    return (dp[j]+sum[j]*sum[j]) - (dp[k]+sum[k]*sum[k]);
}

ll getdown(int j,int k)         //分子
{
    return 2*(sum[j]-sum[k]);
}


int main()
{
    while(~scanf("%d%d",&n,&m))
    {   
        for(int i = 1; i <= n; i++) 
        {
            scanf("%d",&a[i]);
            sum[i] = sum[i-1]+a[i];
        }
        head = rear = 1;        //队首,队尾,向x轴负方向移动
        q[1] = 0;
        for(int i = 1; i <= n; i++) 
        {
            while(head < rear && getup(q[head+1],q[head]) <= getdown(q[head+1],q[head])*sum[i]) head++;
            dp[i] = dp[q[head]] + m + (sum[i]-sum[q[head]])*(sum[i]-sum[q[head]]);
            while(head < rear && getup(q[rear],q[rear-1])*getdown(i,q[rear]) >= getup(i,q[rear])*getdown(q[rear],q[rear-1])) rear--;
            q[++rear] = i;
        }
        printf("%lld\n",dp[n]);
    }
    return 0;
}

参考博客

斜率优化DP
HDU-3507 Print Article(斜率优化DP)