MT2017笔试题
一、大富翁游戏
1、题目
大富翁游戏,玩家根据骰子的点数决定走的步数,即骰子点数为1时可以走一步,点数为2时可以走两步,点数为n时可以走n步。求玩家走到第n步(n<=骰子最大点数且是方法的唯一入参)时,总共有多少种投骰子的方法。
输入描述:
输入包括一个整数n,(1 ≤ n ≤ 6)
输出描述:
输出一个整数,表示投骰子的方法
输入例子1:
6
输出例子1:
32
2、思路
递归思想: 在走了n步时,投骰子的方法f(n)等于
在走了n-1步时投骰子的方法f(n-1)+投一个1
在走了n-2步时投骰子的方法f(n-2)+投一个2
在走了n-3步时投骰子的方法f(n-3)+投一个3
...
在走了1步时投骰子的方法f(1)+投一个n-1
直接投n
所以f(n)=f(n-1)+f(n-2)+f(n-3)...+f(1)+1=2^(n-1)
3、代码
import java.util.Scanner;
/*
考察递归 f(n)=f(n-1)+f(n-2)+......+f(1)+1
*/
public class daFuWeng {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNext()) {
int n = in.nextInt();
int result = method(n);
System.out.println(result);
}
in.close();
}
private static int method(int m) {
int sum = 0;
if (m == 1) {
sum = 1;
} else {
for(int i=1;i<m;i++){
sum += method(m-i);
}
sum=sum+1;
}
return sum;
}
}
二、 拼凑钱币
1、题目
给你六种面额 1、5、10、20、50、100 元的纸币,假设每种币值的数量都足够多,编写程序求组成N元(N为0~10000的非负整数)的不同组合的个数。
输入描述:
输入包括一个整数n(1 ≤ n ≤ 10000)
输出描述:
输出一个整数,表示不同的组合方案数
输入例子1:
1
输出例子1:
1
2、思路
可以用动态规划的方法来求解此问题。动态规划的基本思想就是将待求解问题分解为若干子问题,,先求解这些子问题并将结果保存起来,若在求解较大的问题时用到较小子问题的结果,可以直接取用,从而免去重复计算。

3、代码
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int amount = sc.nextInt();// 钱数
int[] price = {1, 5, 10, 20, 50, 100};// 货币面值
// fun(price, amount);
fun1(price, amount);
}
}
public static void fun1(int[] price, int amount) {
long[][] dp = new long[price.length][amount + 1];
//初始化
for (int i = 0; i < amount + 1; i++) {
dp[0][i] = 1;
}
for (int i = 0; i < price.length; i++) {
dp[i][0] = 1;
}
//计算
for (int i = 1; i < price.length; i++) {
for (int j = 1; j < amount + 1; j++) {
int m = j / price[i];
for (int k = 0; k <= m; k++) {
dp[i][j] += dp[i - 1][j - k * price[i]];
}
}
}
//输出不同的组合方案数
System.out.println(dp[price.length - 1][amount]);
}
}
三、最大矩形面积
1、题目
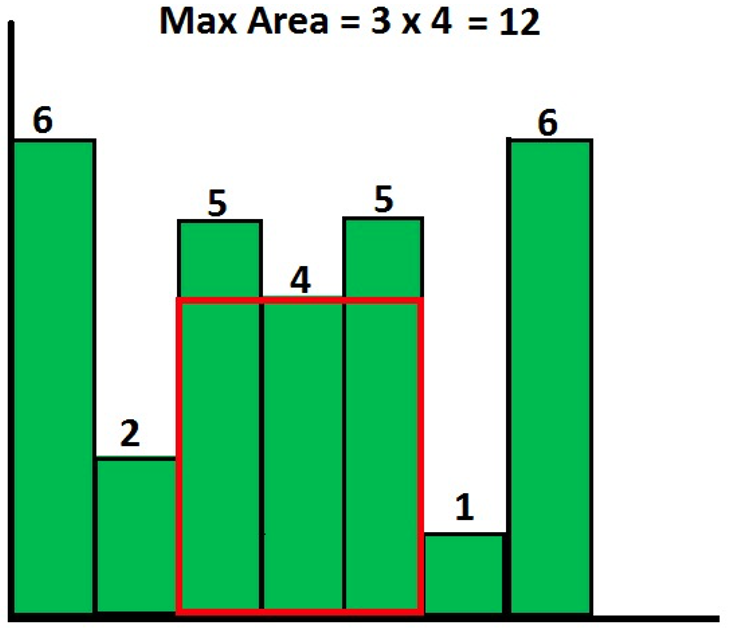
给定一组非负整数组成的数组h,代表一组柱状图的高度,其中每个柱子的宽度都为1。 在这组柱状图中找到能组成的最大矩形的面积(如图所示)。 入参h为一个整型数组,代表每个柱子的高度,返回面积的值。
输入描述:
输入包括两行,第一行包含一个整数n(1 ≤ n ≤ 10000)
第二行包括n个整数,表示h数组中的每个值,h_i(1 ≤ h_i ≤ 1,000,000)
输出描述:
输出一个整数,表示最大的矩阵面积。
输入例子1:
6
2 1 5 6 2 3
输出例子1:
10
2、思路
详见代码部分
3、 代码
import java.util.*;
public class theMaxArea{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
//输入数组长度
int n = sc.nextInt();
//输入数组
int[] height = new int[n];
for(int i = 0; i < n; i++){
height[i] = sc.nextInt();
}
int MaxArea = 0; //存储最大面积
int minH = 0; //存储最小高度
for(int i = 0; i < n; i++){
minH = height[i];
for (int j = i; j < n; j++){
minH = Math.min(minH, height[j]); //找出i之后的最小高度
MaxArea = Math.max(MaxArea, minH * (j - i + 1)); //计算最小高度为高度的最大面积值
}
}
System.out.println(MaxArea);
}
sc.close();
}
}
四、 最长公共连续子串
1、题目
给出两个字符串(可能包含空格),找出其中最长的公共连续子串,输出其长度。
输入描述:
输入为两行字符串(可能包含空格),长度均小于等于50.
输出描述:
输出为一个整数,表示最长公共连续子串的长度。
输入例子1:
abcde
abgde
输出例子1:
2
2、思路
可以用动态规划的方法来求解此问题。详细分析过程见 http://www.cnblogs.com/en-heng/p/3963803.html
3、代码
import java.util.Scanner;
public class theMaxSubLength {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
String str1 = sc.nextLine();
String str2 = sc.nextLine();
int max = lcs(str1, str2);
System.out.println(max);
}
sc.close();
}
public static int lcs(String str1, String str2) {
int len1 = str1.length();
int len2 = str2.length();
int result = 0; //记录最长公共子串长度
int c[][] = new int[len1 + 1][len2 + 1];
for (int i = 0; i <= len1; i++) {
for (int j = 0; j <= len2; j++) {
if (i == 0 || j == 0) {
c[i][j] = 0;
} else if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
c[i][j] = c[i - 1][j - 1] + 1;
result = Math.max(c[i][j], result);
} else {
c[i][j] = 0;
}
}
}
return result;
}
}
-------------------------------
参考链接:
2、牛客网



